Exponents
Exponents are a short way to write repeated multiplication. They help us work with large numbers more easily.
Positive Exponents
Imagine you have a chessboard. You place two grains of wheat on the first square, four grains on the second square, eight grains on the third square, and so on, doubling the number of grains on each next square.
This means there are \(2^{64}\) grains on the last square. Using a calculator:$$2^{64}=18\,446\,744\,073\,709\,551\,616.$$This is an enormous number!

| Square number | Number of grains |
| \(1\) | \(2\) |
| \(2\) | \(2 \times 2\) |
| \(3\) | \(2 \times 2 \times 2\) |
| \(\vdots\) | \(\vdots\) |
| \(64\) | \(\overbrace{2 \times 2 \times \dots \times 2}^{64\ \text{factors}}\) |
This means there are \(2^{64}\) grains on the last square. Using a calculator:$$2^{64}=18\,446\,744\,073\,709\,551\,616.$$This is an enormous number!
Definition Exponentiation
Exponentiation is repeated multiplication of a number by itself.
For a number \(a\) and a positive whole number \(n\),$$a^n = \overbrace{a \times a \times \dots \times a}^{n\ \text{factors}}.$$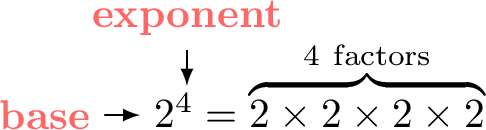
For a number \(a\) and a positive whole number \(n\),$$a^n = \overbrace{a \times a \times \dots \times a}^{n\ \text{factors}}.$$
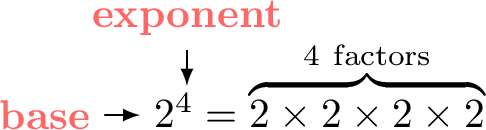
Example
Write using exponent notation: \(5 \times 5 \times 5\).
\(5 \times 5 \times 5 = 5^3\)
Definition Vocabulary
$$\begin{array}{|c|c|c|c|}\hline\text{Value} & \text{Expanded form} & \text{Exponent notation} & \text{Spoken form} \\
\hline2 & 2 & 2^1 & 2\ \text{or}\ 2\ \text{to the power of}\ 1 \\
4 & 2 \times 2 & 2^2 & 2\ \text{squared or}\ 2\ \text{to the power of}\ 2 \\
8 & 2 \times 2 \times 2 & 2^3 & 2\ \text{cubed or}\ 2\ \text{to the power of}\ 3 \\
16 & 2 \times 2 \times 2 \times 2 & 2^4 & 2\ \text{to the power of}\ 4 \\
32 & 2 \times 2 \times 2 \times 2 \times 2 & 2^5 & 2\ \text{to the power of}\ 5 \\
\hline\end{array}$$
Example
Find the value of \(2^3\).
$$\begin{aligned}[t]2^3 &= 2 \times 2 \times 2 \\
&= 8\end{aligned}$$
Negative Exponents
To understand negative exponents, let's explore the pattern of multiplying by \(2\):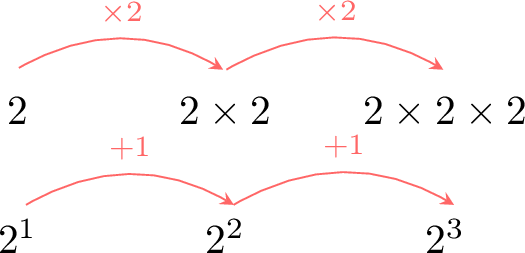


- \(2^1 = 2\)
- \(2^2 = 2 \times 2\)
- \(2^3 = 2 \times 2 \times 2\)

- \(2^0 = 1\)
- \(2^{-1} = \dfrac{1}{2}\)
- \(2^{-2} = \dfrac{1}{2 \times 2}\)
- \(2^{-3} = \dfrac{1}{2 \times 2 \times 2}\)
Definition Exponentiation for a negative exponent
For a non-zero number \(a\) and a positive integer \(n\), we extend exponentiation to negative exponents by:$$\begin{aligned}[t]a^{-n} &= \dfrac{1}{\underbrace{a \times a \times \dots \times a}_{n\ \text{factors}}} \\
&= \dfrac{1}{a^n}\end{aligned} \qquad \text{and} \qquad a^0 = 1 \quad (a \neq 0).$$In particular, \(a^{-1} = \dfrac{1}{a}\). A negative exponent means we take the reciprocal of the corresponding positive power.
Example
Write \(3^{-2}\) as a fraction.
$$\begin{aligned}[t]3^{-2} &= \dfrac{1}{3 \times 3} \\
&= \dfrac{1}{9}\end{aligned}$$
Rational Exponents
We know about positive exponents, like \(5^3 = 5 \times 5 \times 5\), and also about negative exponents, like \(5^{-3} = \dfrac{1}{5 \times 5 \times 5}\).
But what about fractional exponents?
Using the exponent laws, let's see what happens with \(\textcolor{colordef}{5^{\frac{1}{2}}}\):$$\begin{aligned}\textcolor{colordef}{5^{\frac{1}{2}}} \times \textcolor{colordef}{5^{\frac{1}{2}}} &= 5^{\frac{1}{2}+\frac{1}{2}} \\ &= 5^1 \\ &= \textcolor{olive}{5}\end{aligned}$$And by the definition of the square root: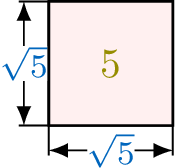
But what about fractional exponents?
Using the exponent laws, let's see what happens with \(\textcolor{colordef}{5^{\frac{1}{2}}}\):$$\begin{aligned}\textcolor{colordef}{5^{\frac{1}{2}}} \times \textcolor{colordef}{5^{\frac{1}{2}}} &= 5^{\frac{1}{2}+\frac{1}{2}} \\ &= 5^1 \\ &= \textcolor{olive}{5}\end{aligned}$$And by the definition of the square root:

Definition Rational Exponent
For a positive number \(a\) and positive integers \(m\) and \(n\),$$\begin{aligned}a^{\frac{1}{2}} &= \sqrt{a}, \\
a^{\frac{1}{n}} &= \sqrt[n]{a}, \\
a^{\frac{m}{n}} &= \sqrt[n]{a^m} = \left(\sqrt[n]{a}\right)^m.\end{aligned}$$
Exercise
Write \(\sqrt{5}\) in exponent form.
$$\sqrt{5} = 5^{\frac{1}{2}}$$
Exponent Law 1
Let's look at an example:$$\begin{aligned}\textcolor{colordef}{7}^{\textcolor{colorprop}{3}} \times \textcolor{colordef}{7}^{\textcolor{olive}{2}}&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}\,\text{factors}} \times \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{olive}{2}\,\text{factors}} \\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}\,\text{factors}} \\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}}.\end{aligned}$$In this example we are multiplying two powers with the same base (7).
We can see that we keep the base and add the exponents: \(3 + 2 = 5\).
In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and multiplied by the same number raised to the power \(\textcolor{olive}{n}\), that is$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}},$$the result is equal to \(\textcolor{colordef}{a}\) raised to the sum of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}.$$
We can see that we keep the base and add the exponents: \(3 + 2 = 5\).
In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and multiplied by the same number raised to the power \(\textcolor{olive}{n}\), that is$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}},$$the result is equal to \(\textcolor{colordef}{a}\) raised to the sum of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}.$$
Proposition Exponent Law 1
When we multiply two powers with the same base, we keep the base and add the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}.$$
$$\begin{aligned}\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}\ \text{factors}} \times \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{olive}{n}\ \text{factors}} \\
&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}\ \text{factors}} \\
&= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}\end{aligned}$$
Example
Simplify \(5^2\times 5^4\).
$$\begin{aligned}\textcolor{colordef}{5}^{\textcolor{colorprop}{2}} \times \textcolor{colordef}{5}^{\textcolor{olive}{4}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2}+\textcolor{olive}{4}} && \text{(same base, add exponents)} \\
&= \textcolor{colordef}{5}^{6}.\end{aligned}$$
Exponent Law 2
Let's look at an example:$$\begin{aligned}\dfrac{\textcolor{colordef}{7}^{\textcolor{colorprop}{5}}}{\textcolor{colordef}{7}^{\textcolor{olive}{2}}}&= \dfrac{\overbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5}\,\text{factors}}} {\underbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}}}_{\textcolor{olive}{2}\,\text{factors}}}\\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}\,\text{factors}}\\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and divided by the same number raised to the power \(\textcolor{olive}{n}\), that is$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}},$$the result is \(\textcolor{colordef}{a}\) raised to the difference of the exponents:$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}.$$
Proposition Exponent Law 2
For \(a\neq 0\) and any numbers \(m\) and \(n\),$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}$$
Example
Simplify \(\dfrac{5^7}{5^3}\).
$$\begin{aligned}\dfrac{\textcolor{colordef}{5}^{\textcolor{colorprop}{7}}}{\textcolor{colordef}{5}^{\textcolor{olive}{3}}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{7} - \textcolor{olive}{3}} \\
&= \textcolor{colordef}{5}^{4}\end{aligned}$$
Exponent Law 3
Let's look at an example:$$\begin{aligned}\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{3}}&= (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})^{\textcolor{olive}{3}} \\
&= \overbrace{(\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})}^{\textcolor{olive}{3}\,\text{factors}} \\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} + \textcolor{colorprop}{2} +\textcolor{colorprop}{2}}\\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{3}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\), and that result is raised to the power \(\textcolor{olive}{n}\), that is$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}},$$the result is \(\textcolor{colordef}{a}\) raised to the product of the exponents:$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}.$$
Proposition Exponent Law 3
For \(a\neq 0\) and any numbers \(m\) and \(n\),$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}$$
Example
Simplify \(\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}}\).
$$\begin{aligned}[t]\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{5}} \\
&= \textcolor{colordef}{5}^{10}\end{aligned}$$
Exponent Law 4
Let's look at an example:$$\begin{aligned}(\textcolor{colordef}{3} \times \textcolor{colorprop}{5})^{\textcolor{olive}{2}}&= (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \times (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \times \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \\
&= (\textcolor{colordef}{3} \times \textcolor{colordef}{3}) \times (\textcolor{colorprop}{5} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3}^{\textcolor{olive}{2}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{2}}\end{aligned}$$In general, when you multiply two numbers \(\textcolor{colordef}{a}\) and \(\textcolor{colorprop}{b}\), and then raise the product to the power \(\textcolor{olive}{n}\), that is$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}},$$the result is each factor raised to the power \(\textcolor{olive}{n}\):$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}.$$
Proposition Exponent Law 4
For any numbers \(n\) and any numbers \(a\) and \(b\),$$\left(\textcolor{colordef}{a}\textcolor{colorprop}{b}\right)^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}$$
Example
Simplify \((\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}}\).
$$(\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}}= \textcolor{colordef}{2}^{\textcolor{olive}{3}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{3}}$$
Exponent Law 5
Let's look at an example:$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \times \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \\
&= \dfrac{\textcolor{colordef}{5} \times \textcolor{colordef}{5}}{\textcolor{colorprop}{3} \times \textcolor{colorprop}{3}} \\
&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}\end{aligned}$$In general, when a quotient \(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\) is raised to a power \(\textcolor{olive}{n}\), that is$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}},$$the result is the numerator raised to that power divided by the denominator raised to that power:$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}}= \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}.$$
Proposition Exponent Law 5
For \(b\neq 0\) and any number \(n\),$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}}= \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}$$
Example
Calculate \(\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}\).
$$\begin{aligned}[t]\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}} \\
&= \dfrac{25}{9}\end{aligned}$$
Exponent Law 6
Let's look at an example with a negative exponent:$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{-2}}&= \dfrac{1}{\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}} \\
&= \dfrac{1}{\dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}} \\
&= 1 \times \dfrac{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}{\textcolor{colordef}{5}^{\textcolor{olive}{2}}} \\
&= \dfrac{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}{\textcolor{colordef}{5}^{\textcolor{olive}{2}}} \\
&= \left(\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{5}}\right)^{\textcolor{olive}{2}}\end{aligned}$$In general, when a quotient \(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\) is raised to a negative power \(\textcolor{olive}{-n}\),$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-n}} = \left(\dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}\right)^{\textcolor{olive}{n}}.$$This means that a negative exponent makes the fraction flip: the numerator and denominator swap places.
Proposition Exponent Law 6
For non-zero numbers \(a\) and \(b\), and any number \(n\),$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-n}} = \left(\dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}\right)^{\textcolor{olive}{n}}$$and in particular,$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-1}} = \dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}.$$
Example
Calculate \(\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{-2}\).
$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{-2} &= \left(\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{5}}\right)^{2} \\
&= \dfrac{3^2}{5^2}\\
&= \dfrac{9}{25} \\
\end{aligned}$$
Order of operations
The order of operations is a set of rules that tells us which calculations to do first in a mathematical expression.
Definition Order of Operations
To solve mathematical expressions accurately, we follow the order of operations, which is commonly remembered using the acronym PEMDAS:
- P: Parentheses
- E: Exponents
- M: Multiplication
- D: Division
- A: Addition
- S: Subtraction
Example
Evaluate \((1+2) \times 2^3 + 4\).
$$\begin{aligned}[t](1+2) \times 2^3 + 4 &= \textcolor{colordef}{(1+2)} \times 2^3 + 4 && (\text{parentheses: } \textcolor{colordef}{(1+2)} = 3) \\
&= 3 \times \textcolor{colordef}{2^3} + 4 && (\text{exponent: } \textcolor{colordef}{2^3} = 8) \\
&= \textcolor{colordef}{3 \times 8} + 4 && (\text{multiplication: } \textcolor{colordef}{3 \times 8} = 24) \\
&= \textcolor{colordef}{24 + 4} && (\text{addition: } \textcolor{colordef}{24 + 4} = 28) \\
&= 28\end{aligned}$$
Scientific Notation
Working with very large or very small numbers can be awkward. Since our number system is base ten, we can use powers of ten to rewrite very large or very small numbers to make them easier to work with. This way of writing numbers is called scientific notation and is especially useful in science.
Definition Scientific Notation
A non-zero number is expressed in scientific notation when it is written in the form:\(a \times 10^n\) where \(1 \leq |a| < 10\) and \(n\) is an integer.
Note
When \(n\) is positive, the number is large (greater than or equal to \(10\) in absolute value). When \(n\) is negative, the number is small (between \(-1\) and \(1\) in absolute value, but not \(0\)).
Example
Write \(245\) in scientific notation.
$$\begin{aligned}[t]245 &= 2.45 \times 100 \\
&= 2.45 \times 10^2\end{aligned}$$So \(245\) in scientific notation is \(2.45 \times 10^2\).
Exponential Expressions
Definition Exponential Expression
An exponential expression is a mathematical expression where a variable appears in the exponent. The base is usually a positive constant different from \(1\).
Example
\(2^x\) and \(5^{x+1}\) are exponential expressions. This is different from a polynomial expression like \(x^2\), where the variable is in the base, not in the exponent.
Method Manipulating Exponential Expressions
Using the laws of exponents (index laws), we can simplify, expand, and factorise expressions where the variable is in the exponent. These skills are fundamental for solving exponential equations.
Example
Simplify \(\displaystyle\frac{2^{x+1}+2^x}{2^x}\).
$$\begin{aligned}[t] \frac{2^{x+1}+2^x}{2^x} &= \frac{2^x \cdot 2^1 + 2^x}{2^x} && \scriptscriptstyle\text{(Using the law }a^{x+1}=a^x\cdot a^1\text{)} \\
&= \frac{2^x(2+1)}{2^x} && \text{(Factor out the common factor } 2^x\text{)} \\
&= 3 && \text{(Simplify the common factor)} \end{aligned}$$
Exponential Equations
Definition Exponential Equation
An exponential equation is an equation in which the unknown occurs in the exponent.
Example
\(2^x = 8\) and \(30 \times 3^x = 7\) are both exponential equations.
There are several methods we can use to solve exponential equations. These include solving by graphing, using technology (such as a calculator or graphing software), and using logarithms, which we will study later. In this section, we focus on equations that can be solved algebraically by rewriting both sides with the same base and then equating the exponents.
Method Solving by Equating Exponents
For \(a>0\), \(a\neq 1\), we have \(a^x = a^y\) if and only if \(x = y\).So, when both sides of an equation can be written with the same base \(a\), we can equate the exponents.
Example
Solve for \(x\):\(2^x = 16\)
$$\begin{aligned}[t]&& 2^x &= 16 \\
\Leftrightarrow && 2^x &= 2^4 && \text{(Write \(16\) as a power of \(2\))} \\
\Leftrightarrow && x &= 4 && \text{(Equate the exponents)}\end{aligned}$$