Affine Transformations
Affine transformations are fundamental geometric operations that map points to points, lines to lines, and planes to planes while preserving parallelism. They are widely used in computer graphics, physics, and robotics to describe movements and deformations. An affine transformation combines a linear transformation (such as rotation, scaling, or reflection) with a translation. In this chapter, we explore how matrices can be used to represent and perform these transformations efficiently in 2D space.
We consider how an object point \((x, y)\), specified by its vector position \(\mathbf{x} = \begin{pmatrix} x \\ y \end{pmatrix}\), is moved to an image point \((x', y')\), specified by its vector position \(\mathbf{x}' = \begin{pmatrix} x' \\ y' \end{pmatrix}\), using matrices.
We consider how an object point \((x, y)\), specified by its vector position \(\mathbf{x} = \begin{pmatrix} x \\ y \end{pmatrix}\), is moved to an image point \((x', y')\), specified by its vector position \(\mathbf{x}' = \begin{pmatrix} x' \\ y' \end{pmatrix}\), using matrices.
Linear Transformations
Definition Linear Transformation in 2D
A transformation \(T\) of the plane is called linear if it maps a point \(P(x, y)\) to an image point \(P'(x', y')\) such that the coordinates satisfy a system of linear equations:$$\begin{cases}x' = ax + by \\
y' = cx + dy\end{cases}$$This can be written in matrix form as:$$\begin{pmatrix} x' \\
y' \end{pmatrix} = \mathbf{A} \begin{pmatrix} x \\
y \end{pmatrix} \quad \text{where} \quad \mathbf{A} = \begin{pmatrix} a & b \\
c & d \end{pmatrix}.$$The matrix \(\mathbf{A}\) is called the transformation matrix.
A key property of linear transformations is that the origin is mapped to itself: \(T(0,0) = (0,0)\). Furthermore, the columns of the matrix \(\mathbf{A}\) reveal where the basis vectors \(\vec{i}=\begin{pmatrix} 1 \\ 0 \end{pmatrix}\) and \(\vec{j}=\begin{pmatrix} 0 \\ 1 \end{pmatrix}\) land.$$ \mathbf{A}\begin{pmatrix} 1 \\
0 \end{pmatrix} = \begin{pmatrix} a \\
c \end{pmatrix} \quad \text{and} \quad \mathbf{A}\begin{pmatrix} 0 \\
1 \end{pmatrix} = \begin{pmatrix} b \\
d \end{pmatrix}. $$This means the first column is the image of \(\vec{i}\) and the second column is the image of \(\vec{j}\).
Example
Find the image of the point \(P(2, 3)\) under the transformation defined by the matrix \(\mathbf{A} = \begin{pmatrix} 2 & 0 \\ 0 & 3 \end{pmatrix}\).
$$\begin{aligned}\begin{pmatrix} x' \\
y' \end{pmatrix} &= \begin{pmatrix} 2 & 0 \\
0 & 3 \end{pmatrix} \begin{pmatrix} 2 \\
3 \end{pmatrix}\\
&= \begin{pmatrix} 2(2) + 0(3) \\
0(2) + 3(3) \end{pmatrix}\\
&= \begin{pmatrix} 4 \\
9 \end{pmatrix} \end{aligned}$$The image is \(P'(4, 9)\). This transformation represents a horizontal stretch by factor 2 and a vertical stretch by factor 3.
Standard Linear Transformations
Definition Scaling/Enlargement
- A horizontal stretch (or stretch parallel to the \(x\)-axis) with scale factor \(k\) is represented by:$$ \mathbf{S}_x = \begin{pmatrix} k & 0 \\ 0 & 1 \end{pmatrix} $$
- A vertical stretch (or stretch parallel to the y-axis) with scale factor \(k\) is represented by:$$ \mathbf{S}_y = \begin{pmatrix} 1 & 0 \\ 0 & k \end{pmatrix} $$
- An enlargement (or scaling) centered at the origin with horizontal scale factor \(k\) and vertical scale factor \(m\) is represented by:$$ \mathbf{S} = \begin{pmatrix} k & 0 \\ 0 & m \end{pmatrix} $$If \(k=m\), it is a uniform enlargement (homothety) with scale factor \(k\).
Example
Find the image of the position vector \(\begin{pmatrix} 2 \\ 3 \end{pmatrix}\) under the horizontal stretch of scale factor \(3\).
The matrix for a horizontal stretch with factor \(k=3\) is \(\mathbf{S} = \begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix}\).$$\begin{aligned}\mathbf{x}' &= \mathbf{S}\mathbf{x} \\
&= \begin{pmatrix} 3 & 0 \\
0 & 1 \end{pmatrix} \begin{pmatrix} 2 \\
3 \end{pmatrix} \\
&= \begin{pmatrix} 3(2) + 0(3) \\
0(2) + 1(3) \end{pmatrix} \\
&= \begin{pmatrix} 6 \\
3 \end{pmatrix}\end{aligned}$$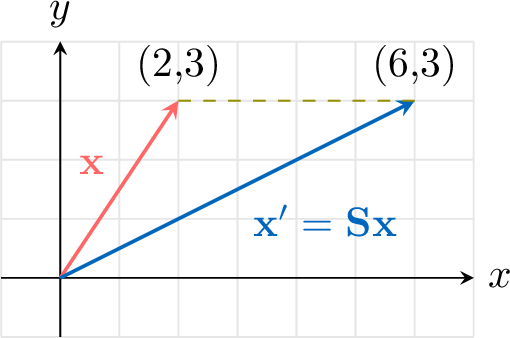
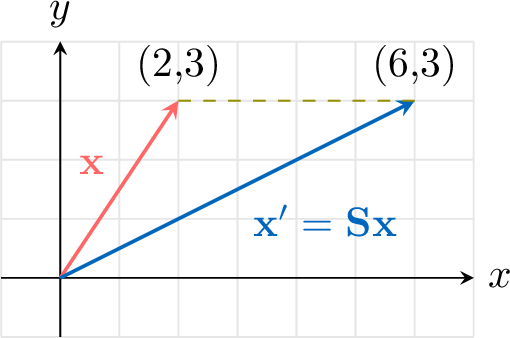
Definition Reflection
- Reflection in the \(x\)-axis: \((x, y) \to (x, -y)\) $$ \mathbf{M}_x = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $$
- Reflection in the \(y\)-axis: \((x, y) \to (-x, y)\) $$ \mathbf{M}_y = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} $$
- Reflection in the line \(y=x\): \((x, y) \to (y, x)\) $$ \mathbf{M}_{y=x} = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} $$
- Reflection in the line \(y=(\tan\theta)x\):$$\mathbf{M}_{y=(\tan\theta)x}=\begin{pmatrix}\cos(2\theta) & \sin(2\theta)\\ \sin(2\theta) & -\cos(2\theta)\end{pmatrix}.$$
Example
Find the image of the position vector \(\begin{pmatrix} 2 \\ 3 \end{pmatrix}\) under reflection in the \(x\)-axis.
The matrix for reflection in the \(x\)-axis is \(\mathbf{M}_x = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\).$$\begin{aligned}\mathbf{x}' &= \mathbf{M}_x\mathbf{x} \\
&= \begin{pmatrix} 1 & 0 \\
0 & -1 \end{pmatrix} \begin{pmatrix} 2 \\
3 \end{pmatrix} \\
&= \begin{pmatrix} 1(2) + 0(3) \\
0(2) + (-1)(3) \end{pmatrix} \\
&= \begin{pmatrix} 2 \\
-3 \end{pmatrix}\end{aligned}$$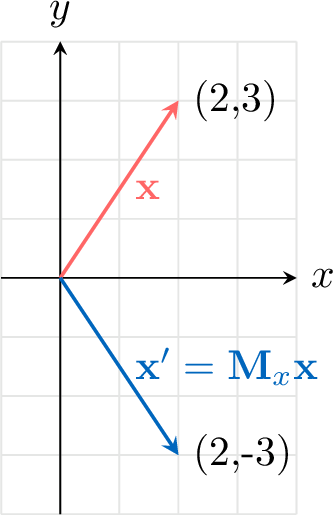
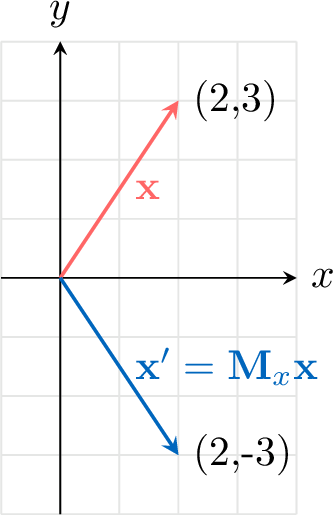
Definition Rotation
A rotation of angle \(\theta\) anti-clockwise about the origin is represented by:$$ \mathbf{R}_{\theta} = \begin{pmatrix} \cos \theta & -\sin \theta \\
\sin \theta & \cos \theta \end{pmatrix} $$
Example
Find the image of the position vector \(\begin{pmatrix} 2 \\ 3 \end{pmatrix}\) under a rotation of \(90^\circ\) (\(\frac{\pi}{2}\) radians) anti-clockwise.
The matrix for rotation of \(90^\circ\) is \(\mathbf{R}_{90^\circ} = \begin{pmatrix} \cos 90^\circ & -\sin 90^\circ \\ \sin 90^\circ & \cos 90^\circ \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\).$$\begin{aligned}\mathbf{x}' &= \mathbf{R}_{90^\circ} \mathbf{x} \\
&= \begin{pmatrix} 0 & -1 \\
1 & 0 \end{pmatrix} \begin{pmatrix} 2 \\
3 \end{pmatrix} \\
&= \begin{pmatrix} 0(2) + (-1)(3) \\
1(2) + 0(3) \end{pmatrix} \\
&= \begin{pmatrix} -3 \\
2 \end{pmatrix}\end{aligned}$$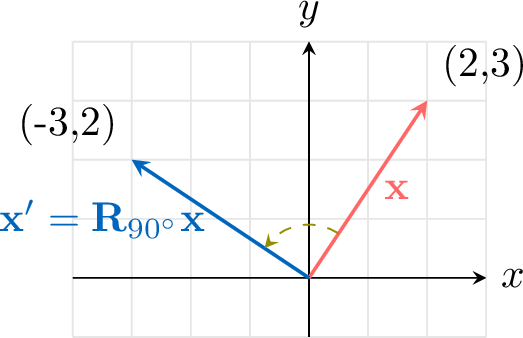

Translation
Definition Translation
A translation by vector \(\mathbf{t} = \begin{pmatrix} e \\ f \end{pmatrix}\) moves every point \(P(x, y)\) to \(P'(x', y')\) according to:$$\begin{pmatrix} x' \\
y' \end{pmatrix} = \begin{pmatrix} x \\
y \end{pmatrix} + \begin{pmatrix} e \\
f \end{pmatrix} = \begin{pmatrix} x+e \\
y+f \end{pmatrix}.$$
This is not a linear transformation (unless \(\mathbf{t}=\mathbf{0}\)) because the origin \((0,0)\) is mapped to \((e, f)\), not itself.
Example
Find the image of the position vector \(\begin{pmatrix} 2 \\ 3 \end{pmatrix}\) under translation by vector \(\begin{pmatrix} 1 \\ -2 \end{pmatrix}\).
$$\begin{aligned}\mathbf{x}' &= \mathbf{x} + \mathbf{t} \\
&= \begin{pmatrix} 2 \\
3 \end{pmatrix} + \begin{pmatrix} 1 \\
-2 \end{pmatrix} \\
&= \begin{pmatrix} 2+1 \\
3+(-2) \end{pmatrix} \\
&= \begin{pmatrix} 3 \\
1 \end{pmatrix}\end{aligned}$$

Affine Transformation
Definition Affine Transformation
An affine transformation is a combination of a linear transformation followed by a translation. It is represented by the matrix equation:$$\mathbf{x}' = \mathbf{A}\mathbf{x} + \mathbf{b}$$where \(\mathbf{x} = \begin{pmatrix} x \\ y \end{pmatrix}\), \(\mathbf{A}\) is a \(2\times 2\) matrix (representing rotation, scaling, shear, etc.), and \(\mathbf{b} = \begin{pmatrix} e \\ f \end{pmatrix}\) is the translation vector.
Example
Find the image of the point \(P(1, 2)\) under an affine transformation consisting of a rotation of \(90^\circ\) anti-clockwise followed by a translation of \(\begin{pmatrix} 3 \\ -1 \end{pmatrix}\).
The rotation matrix is \(\mathbf{R}_{90^\circ} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\). The translation vector is \(\mathbf{b} = \begin{pmatrix} 3 \\ -1 \end{pmatrix}\).$$\begin{aligned}\mathbf{x}' &= \begin{pmatrix} 0 & -1 \\
1 & 0 \end{pmatrix}\begin{pmatrix} 1 \\
2 \end{pmatrix} + \begin{pmatrix} 3 \\
-1 \end{pmatrix}\\
&= \begin{pmatrix} -2 \\
1 \end{pmatrix} + \begin{pmatrix} 3 \\
-1 \end{pmatrix}\\
&= \begin{pmatrix} 1 \\
0 \end{pmatrix}\\
\end{aligned}$$The image point is \((1, 0)\).
Composition of Transformations
Definition Composite Transformation
A composite transformation is the result of applying more than one transformation to an object.
Example
If transformation \(T_1\) has matrix \(\mathbf{A}\) and transformation \(T_2\) has matrix \(\mathbf{B}\), applying \(T_1\) then \(T_2\) corresponds to the matrix multiplication \(\mathbf{B}\mathbf{A}\).$$\begin{aligned} \mathbf{x}' &= T_2(T_1(\mathbf{x}))\\
&= \mathbf{B}(\mathbf{A}\mathbf{x})\\
& = (\mathbf{B}\mathbf{A})\mathbf{x}\end{aligned} $$
Proposition Order Matters
When multiple transformations are applied sequentially, the order matters.
Example
- Find the single matrix that represents a reflection in the \(x\)-axis followed by a rotation of \(90^\circ\) anti-clockwise.
- Find the single matrix that represents a rotation of \(90^\circ\) anti-clockwise followed by a reflection in the \(x\)-axis.
- Compare the results.
Let \(\mathbf{M}_x = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\) be the reflection and \(\mathbf{R}_{90} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\) be the rotation.
- The combined transformation of rotation applied after reflection is$$\begin{aligned}\mathbf{T}_1 &= \mathbf{R}_{90} \mathbf{M}_x \\ &=\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}\\ &= \begin{pmatrix} 0(1)+(-1)(0) & 0(0)+(-1)(-1) \\ 1(1)+0(0) & 1(0)+0(-1) \end{pmatrix}\\ &= \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\\ \end{aligned}$$This represents a reflection in the line \(y=x\).
- The combined transformation of reflection applied after rotation is$$\begin{aligned}\mathbf{T}_2 &= \mathbf{M}_x \mathbf{R}_{90} \\ &=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}\\ &= \begin{pmatrix} 1(0)+0(1) & 1(-1)+0(0) \\ 0(0)+(-1)(1) & 0(-1)+(-1)(0) \end{pmatrix}\\ &= \begin{pmatrix} 0 & -1 \\ -1 & 0 \end{pmatrix}\\ \end{aligned}$$This represents a reflection in the line \(y=-x\).
- We see that \(\mathbf{T}_1 \neq \mathbf{T}_2\). Therefore, the order of transformations matters.
Area and Determinant
Proposition Area Scaling Factor
Let \(\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\) be the matrix of a linear transformation.
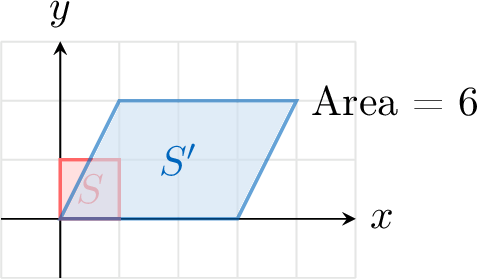
If a shape with area \(S\) is transformed by \(\mathbf{A}\), the area of the image shape \(S'\) is given by:$$ \text{Area}(S') = |\det(\mathbf{A})| \times \text{Area}(S) = |ad-bc| \times \text{Area}(S) $$The absolute value of the determinant represents the area scale factor.
If a shape with area \(S\) is transformed by \(\mathbf{A}\), the area of the image shape \(S'\) is given by:$$ \text{Area}(S') = |\det(\mathbf{A})| \times \text{Area}(S) = |ad-bc| \times \text{Area}(S) $$The absolute value of the determinant represents the area scale factor.
If \(\det(\mathbf{A}) = 1\) or \(-1\), the transformation preserves area (e.g., rotation, reflection).
If \(\det(\mathbf{A}) = 0\), the transformation maps the entire plane onto a line or a point (the area collapses to zero).
If \(\det(\mathbf{A}) = 0\), the transformation maps the entire plane onto a line or a point (the area collapses to zero).
Example
A unit square (Area = 1) is transformed by \(\mathbf{A} = \begin{pmatrix} 3 & 1 \\ 0 & 2 \end{pmatrix}\). Calculate the area of the image.
$$ \det(\mathbf{A}) = (3)(2) - (1)(0) = 6. $$The area of the image is \(|6| \times 1 = 6\).