Matrices
Matrices are rectangular arrays of numbers that provide a powerful tool for solving systems of linear equations and representing linear transformations. Just as complex numbers extend the real number line, matrices can be seen as an extension of the concept of number to higher dimensions. This chapter introduces the algebraic foundations of matrices, their operations, and their fundamental role in various mathematical and scientific applications. Unless stated otherwise, matrix entries are real numbers.
Structure
Definition
Definition Matrix
A matrix \(\mathbf{A}\) of size \(n\times p\) is a rectangular array of numbers with \(n\) rows and \(p\) columns:$$\mathbf{A}=\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1p}\\
a_{21} & a_{22} & \cdots & a_{2p}\\
\vdots & \vdots & & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{np}\\
\end{pmatrix}.$$\(a_{ij}\) is called the entry or element of \(\mathbf{A}\) at position \((i,j)\) (in the \(i\)-th row and \(j\)-th column).
Example
\(\mathbf{A}=\begin{pmatrix}1&3&5 \\7&2&6\\ \end{pmatrix}\) has 2 rows and 3 columns, so its size is \(2\times 3\).
\(a_{\textcolor{colordef}{1}\textcolor{colorprop}{3}}\) is equal to \(5\). It is the entry in row \(\textcolor{colordef}{1}\) and column \(\textcolor{colorprop}{3}\).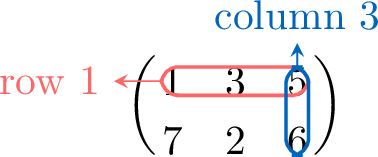
\(a_{\textcolor{colordef}{1}\textcolor{colorprop}{3}}\) is equal to \(5\). It is the entry in row \(\textcolor{colordef}{1}\) and column \(\textcolor{colorprop}{3}\).
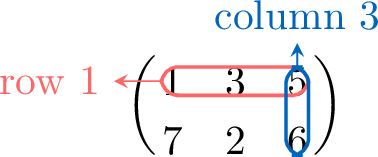
Special Matrices
Definition Column Matrix
A matrix with one column, \(\begin{pmatrix}c_{1}\\c_{2}\\ \vdots\\c_{n} \end{pmatrix}\), is called a column matrix or column vector.
Example
\(C=\begin{pmatrix}1\\3 \\-1\\\end{pmatrix}\) has 3 rows and 1 column. \(C\) is a column matrix of size \(3\times 1\).
Definition Row Matrix
A matrix with one row, \(\begin{pmatrix}r_{1}&r_{2}& \dots &r_{p} \end{pmatrix}\), is called a row matrix or row vector.
Example
\(R=\begin{pmatrix}1&3 &-1\\\end{pmatrix}\) has 1 row and 3 columns. \(R\) is a row matrix of size \(1\times 3\).
Definition Square Matrix
A matrix with the same number of rows and columns is called a square matrix. A square matrix of size \(n \times n\) is said to be of order \(n\):$$\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}\\
\end{pmatrix}.$$
Example
\(\mathbf{A}=\begin{pmatrix}1&3 \\2&5\end{pmatrix}\) has 2 rows and 2 columns. \(\mathbf{A}\) is a square matrix of order \(2\).
Definition Zero Matrix
A matrix where all entries are zero is called a zero matrix or null matrix.
It is denoted \(0_{n,p}\) if it has \(n\) rows and \(p\) columns, or simply \(0\) if the size is clear from the context.
It is denoted \(0_{n,p}\) if it has \(n\) rows and \(p\) columns, or simply \(0\) if the size is clear from the context.
Example
\(0_{2,3}=\begin{pmatrix}0&0&0 \\0&0&0\end{pmatrix}\).
Definition Identity Matrix
The identity matrix, denoted \(I_n\), is a square matrix of order \(n\) with ones on the main diagonal and zeros elsewhere:$$I_n=\begin{pmatrix}1&0&\cdots &0\\
0&1&\ddots &\vdots \\
\vdots &\ddots &\ddots &0\\
0&\cdots &0&1\end{pmatrix}.$$
Example
\(I_3=\begin{pmatrix}1&0&0 \\0&1&0\\0 & 0 &1 \\\end{pmatrix}\) is the identity matrix of order \(3\).
Definition Opposite Matrix
The opposite matrix of \(\mathbf{A}\), denoted \(-\mathbf{A}\), is the matrix where each entry is the additive inverse of the corresponding entry in \(\mathbf{A}\):$$-\mathbf{A}=\begin{pmatrix}-a_{11} & \cdots & -a_{1p}\\
\vdots & & \vdots\\
-a_{n1} & \cdots & -a_{np}\end{pmatrix}.$$
Example
Find the opposite matrix of \(\mathbf{A}=\begin{pmatrix}1&3&-5 \\7&-2&6\\ \end{pmatrix}\).
\(-\mathbf{A}=\begin{pmatrix}-1&-3&5 \\-7&2&-6\\ \end{pmatrix}\)
Equality
Definition Equality of Matrices
Two matrices \(A\) and \(B\) are equal, written as \(A = B\), if they have:
- the same number of rows,
- the same number of columns,
- and their corresponding entries are equal.
Example
$$\begin{pmatrix}1^2&2^2\\
3^2&4^2\end{pmatrix}=\begin{pmatrix}1&4\\
9&16\end{pmatrix}$$and$$\begin{pmatrix}0&0\\
0&0\\
0&0\\
\end{pmatrix}\neq\begin{pmatrix}0&0\\
0&0\\
\end{pmatrix}$$
Matrix Operations
Matrix Addition
Definition Matrix Addition
Let \(\mathbf{A}\) and \(B\) be two matrices of the same size \(n\times p\).
The sum \(\mathbf{A}+B\) is the matrix obtained by adding the corresponding entries of \(\mathbf{A}\) and \(B\):$$\begin{pmatrix}a_{11} & \cdots & a_{1p}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{np}\end{pmatrix}+\begin{pmatrix}b_{11} & \cdots & b_{1p}\\ \vdots & & \vdots\\ b_{n1} & \cdots & b_{np}\end{pmatrix}=\begin{pmatrix}a_{11}+b_{11} & \cdots & a_{1p}+b_{1p}\\ \vdots & & \vdots\\ a_{n1}+b_{n1} & \cdots & a_{np}+b_{np}\end{pmatrix}.$$
The sum \(\mathbf{A}+B\) is the matrix obtained by adding the corresponding entries of \(\mathbf{A}\) and \(B\):$$\begin{pmatrix}a_{11} & \cdots & a_{1p}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{np}\end{pmatrix}+\begin{pmatrix}b_{11} & \cdots & b_{1p}\\ \vdots & & \vdots\\ b_{n1} & \cdots & b_{np}\end{pmatrix}=\begin{pmatrix}a_{11}+b_{11} & \cdots & a_{1p}+b_{1p}\\ \vdots & & \vdots\\ a_{n1}+b_{n1} & \cdots & a_{np}+b_{np}\end{pmatrix}.$$
Example
\(\begin{aligned}[t]\begin{pmatrix}0 &1 & 2 \\3 &4 & 5 \\\end{pmatrix}+\begin{pmatrix}-2 &-1 & 1 \\0 & 1 & 0 \\\end{pmatrix}&=\begin{pmatrix}0-2 &1-1 & 2+1\\3+0 & 4+1 & 5+0\\\end{pmatrix}\\&=\begin{pmatrix}-2 &0 & 3\\3 & 5 & 5\\\end{pmatrix}\end{aligned}\)
Proposition Properties of Matrix Addition
Let \(\mathbf{A}, B, C\) be three matrices of the same size.
- Commutativity: \(\mathbf{A}+B=B+\mathbf{A}\)
- Associativity: \((\mathbf{A}+B)+C=\mathbf{A}+(B+C)\)
- Identity Element: The zero matrix \(0\) is the identity element for addition: \(\mathbf{A}+0=0+\mathbf{A}=\mathbf{A}\)
- Inverse Element: \(\mathbf{A}+(-\mathbf{A})=0\).
As with real numbers, subtraction is defined as adding the opposite matrix, which is equivalent to subtracting the corresponding entries one by one.
Definition Matrix Subtraction
Let \(\mathbf{A}\) and \(B\) be two matrices of the same size \(n\times p\).
The difference \(\mathbf{A}-B\) is the matrix obtained by subtracting the corresponding entries of \(B\) from \(\mathbf{A}\):$$\mathbf{A} - B = \mathbf{A} + (-B).$$
The difference \(\mathbf{A}-B\) is the matrix obtained by subtracting the corresponding entries of \(B\) from \(\mathbf{A}\):$$\mathbf{A} - B = \mathbf{A} + (-B).$$
Example
\(\begin{aligned}[t]\begin{pmatrix}0 &1 \\3 &4 \\\end{pmatrix}-\begin{pmatrix}-2 &-1 \\0 & 1 \\\end{pmatrix}&=\begin{pmatrix}0-(-2) &1-(-1)\\3-0 & 4-1\\\end{pmatrix}\\&=\begin{pmatrix}2 &2\\3 & 3\\\end{pmatrix}\end{aligned}\)
Scalar Multiplication
Definition Scalar Multiplication
Let \(\mathbf{A}\) be a matrix of size \(n\times p\) and \(\lambda\) be a scalar.
The product \(\lambda \mathbf{A}\) is the matrix obtained by multiplying each entry of \(\mathbf{A}\) by \(\lambda\):$$\lambda \begin{pmatrix}a_{11} & \cdots & a_{1p}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{np}\end{pmatrix}=\begin{pmatrix}\lambda a_{11} & \cdots & \lambda a_{1p}\\ \vdots & & \vdots\\ \lambda a_{n1} & \cdots & \lambda a_{np}\end{pmatrix}.$$
The product \(\lambda \mathbf{A}\) is the matrix obtained by multiplying each entry of \(\mathbf{A}\) by \(\lambda\):$$\lambda \begin{pmatrix}a_{11} & \cdots & a_{1p}\\ \vdots & & \vdots\\ a_{n1} & \cdots & a_{np}\end{pmatrix}=\begin{pmatrix}\lambda a_{11} & \cdots & \lambda a_{1p}\\ \vdots & & \vdots\\ \lambda a_{n1} & \cdots & \lambda a_{np}\end{pmatrix}.$$
Example
\(\begin{aligned}[t]2\begin{pmatrix}0 &1 & 2 \\3 &4 & 5 \\\end{pmatrix}&=\begin{pmatrix}2\times 0 &2\times 1 & 2\times 2 \\2\times 3 &2\times 4 & 2\times 5 \\\end{pmatrix}\\&=\begin{pmatrix}0 &2 & 4 \\6 &8 & 10 \\\end{pmatrix}\end{aligned}\)
Proposition Properties of Scalar Multiplication
Let \(\mathbf{A},B\) be two matrices of the same size and \(\lambda,\mu\) be two scalars.
Then,
Then,
- \(\lambda(\mathbf{A} + B) = \lambda \mathbf{A} + \lambda B\)
- \((\lambda+ \mu)\mathbf{A} = \lambda \mathbf{A} + \mu \mathbf{A}\)
- \((\lambda \mu)\mathbf{A} = \lambda(\mu \mathbf{A})\)
- \(1\cdot \mathbf{A}=\mathbf{A}\)
Matrix Multiplication
Definition Matrix Multiplication
Let \(\mathbf{A}\) be a matrix of size \(n\times p\) and \(B\) be a matrix of size \(p\times q\).
The matrix product \(\mathbf{A} \times B\) is a matrix \(C\) of size \(n\times q\) where the entry \(c_{ij}\) is the dot product of the \(i\)-th row of \(\mathbf{A}\) and the \(j\)-th column of \(B\):$$c_{ij}=\sum_{k=1}^p a_{ik}b_{kj}, \qquad 1 \leqslant i \leqslant n,\; 1 \leqslant j \leqslant q.$$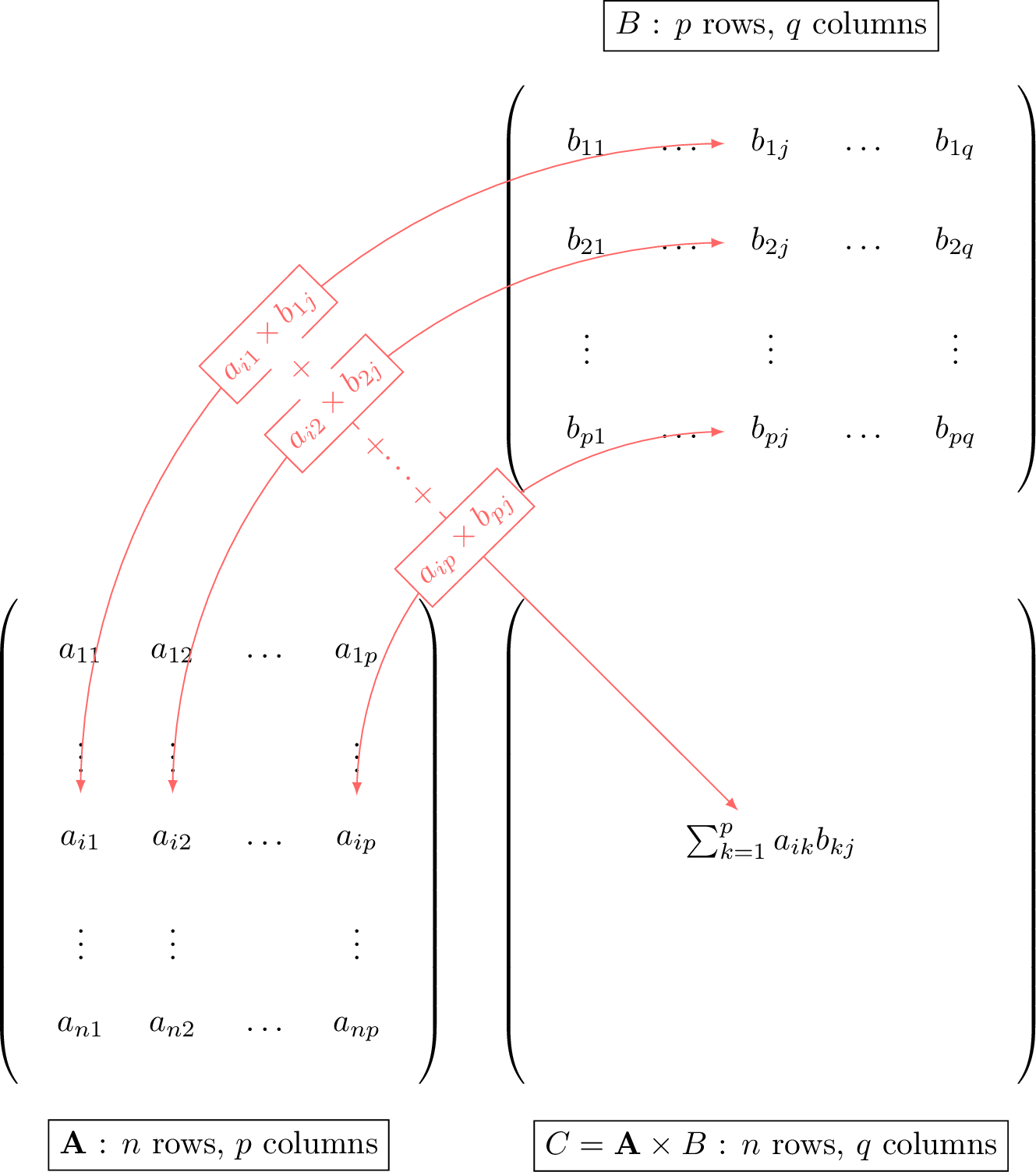
The matrix product \(\mathbf{A} \times B\) is a matrix \(C\) of size \(n\times q\) where the entry \(c_{ij}\) is the dot product of the \(i\)-th row of \(\mathbf{A}\) and the \(j\)-th column of \(B\):$$c_{ij}=\sum_{k=1}^p a_{ik}b_{kj}, \qquad 1 \leqslant i \leqslant n,\; 1 \leqslant j \leqslant q.$$

Example
\(\begin{aligned}[t]\begin{pmatrix}\color{orange}2 &\color{orange}3 \\\color{colordef}1 &\color{colordef}0 \\\end{pmatrix}\begin{pmatrix}\color{colorprop}1 & \color{olive}2 \\\color{colorprop}3 &\color{olive}4 \\\end{pmatrix}&=\begin{pmatrix}\color{orange}2\color{black}\times \color{colorprop} 1\color{black}+\color{orange}3\color{black}\times \color{colorprop} 3 \color{black}&\color{orange}2\color{black}\times \color{olive}2\color{black}+\color{orange}3\color{black}\times \color{olive}4 \color{black} \\\color{colordef}1\color{black}\times \color{colorprop} 1\color{black}+\color{colordef}0\color{black}\times \color{colorprop} 3 \color{black}&\color{colordef}1\color{black}\times \color{olive}2\color{black}+\color{colordef}0\color{black}\times \color{olive}4 \color{black}\end{pmatrix}\\&=\begin{pmatrix}11 &16\\1 &2\\\end{pmatrix}\end{aligned}\)
In general, matrix multiplication is not commutative (\(\mathbf{A}B \neq B\mathbf{A}\)). For example, if \(\mathbf{A}=\begin{pmatrix}0&1\\0&0\\\end{pmatrix}\) and \(B=\begin{pmatrix}1&0\\0&0\\\end{pmatrix}\), then \(\mathbf{A}\times B=\begin{pmatrix}0&0\\0&0\\\end{pmatrix}\) while \(B\times \mathbf{A} = \begin{pmatrix}0&1\\0&0\\\end{pmatrix}\).
Furthermore, the product of two non-zero matrices can be the zero matrix. For example,$$\begin{pmatrix}0&1\\ 0&0\\ \end{pmatrix}\times\begin{pmatrix}1&0\\ 0&0\\ \end{pmatrix}=\begin{pmatrix}0&0\\ 0&0\\ \end{pmatrix}.$$
Furthermore, the product of two non-zero matrices can be the zero matrix. For example,$$\begin{pmatrix}0&1\\ 0&0\\ \end{pmatrix}\times\begin{pmatrix}1&0\\ 0&0\\ \end{pmatrix}=\begin{pmatrix}0&0\\ 0&0\\ \end{pmatrix}.$$
Proposition Properties of Matrix Multiplication
Assume all the following products are defined (sizes are compatible).
- Associativity: $$ (\mathbf{A}B)C = \mathbf{A}(BC)$$
- Distributivity over addition:$$ ( \mathbf{A} + B) C = \mathbf{A}C + BC \quad\text{ and }\quad \mathbf{A}(B+ C) = \mathbf{A}B + \mathbf{A}C $$
- Identity Element: The identity matrix is the neutral element for multiplication. For any matrix \(\mathbf{A}\) of size \(n \times p\), we have: $$I_n \mathbf{A} =\mathbf{A} I_p = \mathbf{A}$$
Invertible Matrices
Definition
We know how to solve an equation \(ax = b\) with real coefficients. If \(a\neq 0\), the unique solution is \(x=a^{-1}b\). To find the solution, we consider the existence of the inverse of \(a\). For matrices, solving \(\mathbf{A}\mathbf{x} = B\) raises the same question about the existence of the inverse of \(\mathbf{A}\).
Definition Inverse of a Matrix
Let \(\mathbf{A}\) be a square matrix of order \(n\).
We say that \(\mathbf{A}\) is invertible if there exists a square matrix \(B\) of order \(n\) such that$$\mathbf{A}B=B\mathbf{A}=I_n.$$If it exists, the matrix \(B\) is unique and called the inverse of \(\mathbf{A}\), denoted \(\mathbf{A}^{-1}\).
An invertible matrix is also called a non-singular matrix. A square matrix that is not invertible is called a singular matrix.
We say that \(\mathbf{A}\) is invertible if there exists a square matrix \(B\) of order \(n\) such that$$\mathbf{A}B=B\mathbf{A}=I_n.$$If it exists, the matrix \(B\) is unique and called the inverse of \(\mathbf{A}\), denoted \(\mathbf{A}^{-1}\).
An invertible matrix is also called a non-singular matrix. A square matrix that is not invertible is called a singular matrix.
Example
The inverse of the identity matrix is itself, because \(I_nI_n=I_n\).
Finding the Inverse of a 2x2 Matrix
Definition Determinant of a 2x2 Matrix
Let \(\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\) be a square matrix of order \(2\).
The determinant of \(\mathbf{A}\) is \(ad-bc\). It is denoted \(\det(\mathbf{A})\).
The determinant of \(\mathbf{A}\) is \(ad-bc\). It is denoted \(\det(\mathbf{A})\).
Example
Calculate the determinant of the matrix \(\mathbf{A} = \begin{pmatrix} 5 & 2 \\ 3 & 4 \end{pmatrix}\).
For the matrix \(\mathbf{A} = \begin{pmatrix} 5 & 2 \\ 3 & 4 \end{pmatrix}\), we have \(a=5\), \(b=2\), \(c=3\), and \(d=4\).$$\begin{aligned}\det(\mathbf{A}) &= ad-bc\\
&=(5)(4) - (2)(3) \\
&= 20 - 6 \\
&= 14\end{aligned}$$
Proposition Invertibility of a 2x2 Matrix
Let \(\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\) be a square matrix of order \(2\).
\(\mathbf{A}\) is invertible if and only if \(\det(\mathbf{A})\neq 0\).
In that case,$$\mathbf{A}^{-1}=\dfrac{1}{\det(\mathbf{A})}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}.$$
\(\mathbf{A}\) is invertible if and only if \(\det(\mathbf{A})\neq 0\).
In that case,$$\mathbf{A}^{-1}=\dfrac{1}{\det(\mathbf{A})}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}.$$
Let \(\mathbf{A} = \begin{pmatrix} a & b \\ c & d \end{pmatrix}\).
- If \(\mathbf{A}\) is invertible, then \(\det(\mathbf{A})\neq 0\).
Assume that \(\mathbf{A}\) is invertible and let$$\mathbf{A}^{-1} = \begin{pmatrix} w & x \\ y & z \end{pmatrix}.$$The condition \(\mathbf{A}\mathbf{A}^{-1} = I_2\) gives$$\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix} w & x \\ y & z \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\Rightarrow\begin{pmatrix} aw+by & ax+bz \\ cw+dy & cx+dz \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}.$$By identification, we obtain two systems:$$\begin{cases} aw+by = 1 \quad (1) \\ cw+dy = 0 \quad (2)\end{cases}\quad \text{and} \quad\begin{cases} ax+bz = 0 \quad (3) \\ cx+dz = 1 \quad (4)\end{cases}$$Suppose now that \(ad-bc=0\).
Multiply (1) by \(d\) and (2) by \(b\), then subtract:$$(ad-bc)w = d.$$Since \(ad-bc=0\), this implies \(d=0\). By combining (1) and (2) differently, and similarly (3) and (4), one also obtains \(a=b=c=0\). Equation (1) would then read \(0=1\), which is a contradiction. Hence \(ad-bc\neq 0\), that is, \(\det(\mathbf{A})\neq 0\). - If \(\det(\mathbf{A})\neq 0\), then \(\mathbf{A}\) is invertible.
Assume now that \(ad-bc\neq 0\). Set$$B=\dfrac{1}{ad-bc}\begin{pmatrix} d & -b \\ -c & a \end{pmatrix}.$$A direct computation shows that$$\mathbf{A}B = B\mathbf{A} = I_2.$$Therefore \(B\) is the inverse of \(\mathbf{A}\) and \(\mathbf{A}\) is invertible.
Applications
Solving Systems of Linear Equations
The sum of the heights of a son and his father is \(2.5\) meters. The difference in their heights is \(0.5\) meters. What are their heights?
The first step is to model this with a system of linear equations.
Let the variable \(x\) represent the son's height and \(y\) represent the father's height.
The pair \((x,y)\) satisfies the following system:$$(S)\quad \begin{cases}x+y&=2.5\\ -x+y&=0.5\end{cases}$$We can solve a single linear equation with real coefficients, like \(2x=4\), by multiplying by the inverse of \(2\) to get \(x=2\).
An idea is to transform the system of two equations with two unknowns into a single equation with one unknown. This transformation involves an abstraction of the nature of the coefficients and variables: from real numbers to arrays of numbers (matrices).
The equivalent matrix equation is$$\mathbf{A}\mathbf{x} =B$$with \(\mathbf{A}=\begin{pmatrix} 1 & 1 \\ -1 & 1 \\\end{pmatrix}\), \(\mathbf{x}=\begin{pmatrix} x \\ y \\\end{pmatrix}\) and \(B=\begin{pmatrix} 2.5 \\ 0.5 \\\end{pmatrix}\).
The matrix \(\mathbf{A}\) is invertible. This means there exists a matrix \(\mathbf{A}^{-1}=\begin{pmatrix} \frac 1 2 & -\frac 1 2 \\ \frac 1 2 & \frac 1 2 \\\end{pmatrix}\) such that, by multiplying both sides of the equation \(\mathbf{A}\mathbf{x} =B\) on the left by \(\mathbf{A}^{-1}\), we get:$$ \mathbf{x}=\mathbf{A}^{-1} B.$$Thus,$$ \begin{pmatrix} x \\ y \\ \end{pmatrix}=\begin{pmatrix} \frac 1 2 & -\frac 1 2 \\ \frac 1 2 & \frac 1 2 \\ \end{pmatrix}\begin{pmatrix} 2.5 \\ 0.5 \\ \end{pmatrix}=\begin{pmatrix} 1 \\ 1.5 \\ \end{pmatrix}.$$By identification, the unique solution is \(x=1\) and \(y=1.5\).
The first step is to model this with a system of linear equations.
Let the variable \(x\) represent the son's height and \(y\) represent the father's height.
The pair \((x,y)\) satisfies the following system:$$(S)\quad \begin{cases}x+y&=2.5\\ -x+y&=0.5\end{cases}$$We can solve a single linear equation with real coefficients, like \(2x=4\), by multiplying by the inverse of \(2\) to get \(x=2\).
An idea is to transform the system of two equations with two unknowns into a single equation with one unknown. This transformation involves an abstraction of the nature of the coefficients and variables: from real numbers to arrays of numbers (matrices).
The equivalent matrix equation is$$\mathbf{A}\mathbf{x} =B$$with \(\mathbf{A}=\begin{pmatrix} 1 & 1 \\ -1 & 1 \\\end{pmatrix}\), \(\mathbf{x}=\begin{pmatrix} x \\ y \\\end{pmatrix}\) and \(B=\begin{pmatrix} 2.5 \\ 0.5 \\\end{pmatrix}\).
The matrix \(\mathbf{A}\) is invertible. This means there exists a matrix \(\mathbf{A}^{-1}=\begin{pmatrix} \frac 1 2 & -\frac 1 2 \\ \frac 1 2 & \frac 1 2 \\\end{pmatrix}\) such that, by multiplying both sides of the equation \(\mathbf{A}\mathbf{x} =B\) on the left by \(\mathbf{A}^{-1}\), we get:$$ \mathbf{x}=\mathbf{A}^{-1} B.$$Thus,$$ \begin{pmatrix} x \\ y \\ \end{pmatrix}=\begin{pmatrix} \frac 1 2 & -\frac 1 2 \\ \frac 1 2 & \frac 1 2 \\ \end{pmatrix}\begin{pmatrix} 2.5 \\ 0.5 \\ \end{pmatrix}=\begin{pmatrix} 1 \\ 1.5 \\ \end{pmatrix}.$$By identification, the unique solution is \(x=1\) and \(y=1.5\).
Proposition Matrix Representation
A linear system of the form$$\begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \\
a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \\
\quad\quad\quad\quad\quad\vdots \\
a_{n1}x_1 + a_{n2}x_2 + \dots + a_{nn}x_n = b_n\end{cases}$$is equivalent to the equation \(\mathbf{A}\mathbf{x} = B\) where$$\mathbf{A} = \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\
\vdots & \vdots & & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}\\
\end{pmatrix}$$is a square matrix of order \(n\), and$$\mathbf{x} = \begin{pmatrix}x_{1}\\
\vdots \\
x_{n}\\
\end{pmatrix}, \quad B = \begin{pmatrix}b_{1}\\
\vdots \\
b_{n}\\
\end{pmatrix}$$are column matrices (column vectors).
Example
Write the system \(\begin{cases}2x+5y&=2\\x+3y&=5\end{cases}\) in matrix form.
In matrix form, the system is$$\begin{pmatrix}2 & 5 \\
1 & 3 \\
\end{pmatrix}\begin{pmatrix} x \\
y \\
\end{pmatrix}=\begin{pmatrix} 2 \\
5 \\
\end{pmatrix}.$$
Proposition
If \(\mathbf{A}\) is invertible, then the equation \(\mathbf{A}\mathbf{x} = B\) has the unique solution \(\mathbf{x} = \mathbf{A}^{-1}B\).
$$\begin{aligned}\mathbf{A}\mathbf{x} &= B\\
\mathbf{A}^{-1}(\mathbf{A}\mathbf{x}) &= \mathbf{A}^{-1}B && \text{(multiply both sides on the left by } \mathbf{A}^{-1}\text{)}\\
(\mathbf{A}^{-1}\mathbf{A})\mathbf{x} &= \mathbf{A}^{-1}B && \text{(associativity)} \\
I_n\mathbf{x} &= \mathbf{A}^{-1}B && \text{(definition of inverse)} \\
\mathbf{x} &= \mathbf{A}^{-1}B && \text{(property of the identity matrix)}\end{aligned}$$
Example
Solve the system$$\begin{pmatrix}2 & 5 \\
1 & 3 \\
\end{pmatrix}\begin{pmatrix} x \\
y \\
\end{pmatrix}=\begin{pmatrix} 2 \\
5 \\
\end{pmatrix}.$$
- Find the inverse: Since \(\det(\mathbf{A}) = (2)(3) - (5)(1) = 6 - 5 = 1 \neq 0\), the matrix \(\mathbf{A}\) is invertible. $$ \mathbf{A}^{-1} = \frac{1}{1} \begin{pmatrix} 3 & -5 \\ -1 & 2 \end{pmatrix} = \begin{pmatrix} 3 & -5 \\ -1 & 2 \end{pmatrix}. $$
- Find the solution:$$\begin{aligned}\begin{pmatrix} x \\ y \\ \end{pmatrix}&=\begin{pmatrix} 3 & -5 \\ -1 & 2 \end{pmatrix}\begin{pmatrix} 2 \\ 5 \\ \end{pmatrix}\\ &=\begin{pmatrix} (3)(2)+(-5)(5) \\ (-1)(2)+(2)(5) \\ \end{pmatrix}\\ &=\begin{pmatrix} -19 \\ 8 \\ \end{pmatrix}.\end{aligned}$$The solution is \(x = -19\) and \(y=8\).