Expansion of Algebraic Expressions
In algebra, expressions can be written in different forms. A factored form represents an expression as a product, like \(a(b+c)\). An expanded form represents it as a sum of terms, like \(ab+ac\).
Expanding is the algebraic process of converting a factored form into an expanded form. In practice, this means removing the brackets by multiplying the factor outside by each term inside. This is a fundamental skill used for simplifying expressions and solving equations.
Expanding is the algebraic process of converting a factored form into an expanded form. In practice, this means removing the brackets by multiplying the factor outside by each term inside. This is a fundamental skill used for simplifying expressions and solving equations.
Distributive Law 1
Proposition Distributive Law
Multiplication is distributive over addition and subtraction:
- Addition:
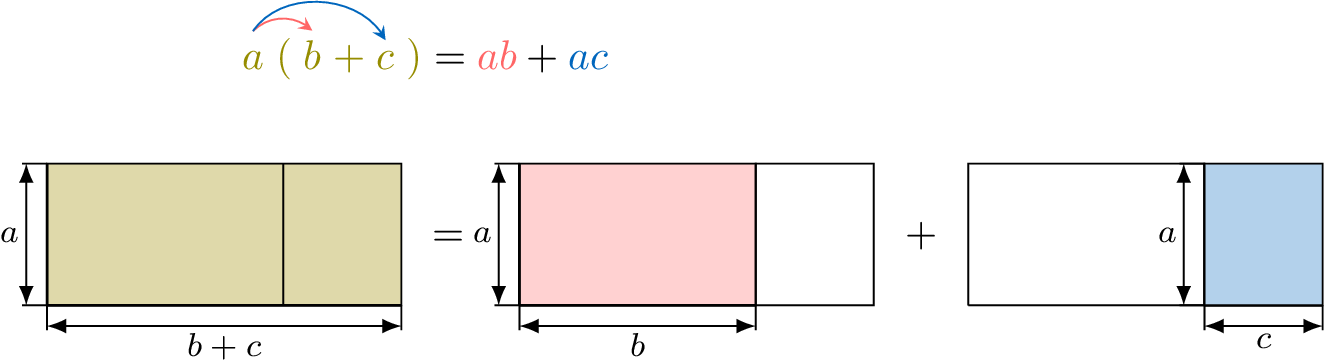
- Subtraction:
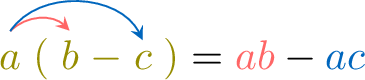
Example
Show that \(2(\ell + L) = 2\ell + 2L\).
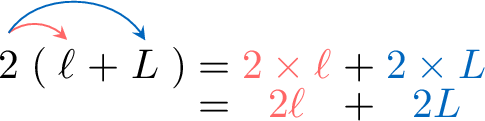
Distributive Law 2
Proposition Distributive Law 2
Each term in the first bracket multiplies each term in the second bracket. 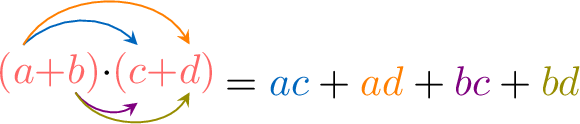

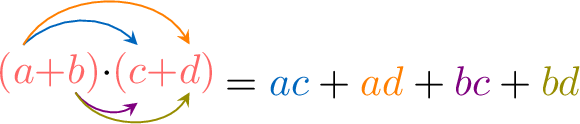

Example
Expand and simplify \((x+4)(2x+2)\).
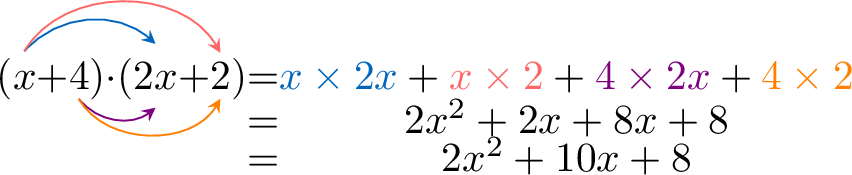
Difference of Two Squares
Proposition Difference of Two Squares
$$(\textcolor{colordef}{a}-\textcolor{colorprop}{b})(\textcolor{colordef}{a}+\textcolor{colorprop}{b}) =\textcolor{colordef}{a}^2-\textcolor{colorprop}{b}^2 $$This identity is called the difference of two squares.
$$\begin{aligned}(a-b)(a+b) &= a(a+b)-b(a+b) &&\text{(distributive law)} \\
&= a^2+ab-ab-b^2 &&\text{(expanding)} \\
&= a^2+\cancel{ab}-\cancel{ab}-b^2 && \\
&= a^2-b^2. &&\end{aligned}$$
Example
Expand and simplify: \((x-3)(x+3)\).
$$\begin{aligned}(\textcolor{colordef}{x}-\textcolor{colorprop}{3})(\textcolor{colordef}{x}+\textcolor{colorprop}{3}) & = \textcolor{colordef}{x}^2-\textcolor{colorprop}{3}^2 \\
& = x^2-9.\end{aligned}$$So \((x-3)(x+3)=x^2-9\).
Perfect Squares Expansion
Proposition Perfect Squares Expansion
The square of a sum and the square of a difference can be written as:$$(a+b)^2=a^2+2ab+b^2 \quad\text{and}\quad (a-b)^2=a^2-2ab+b^2.$$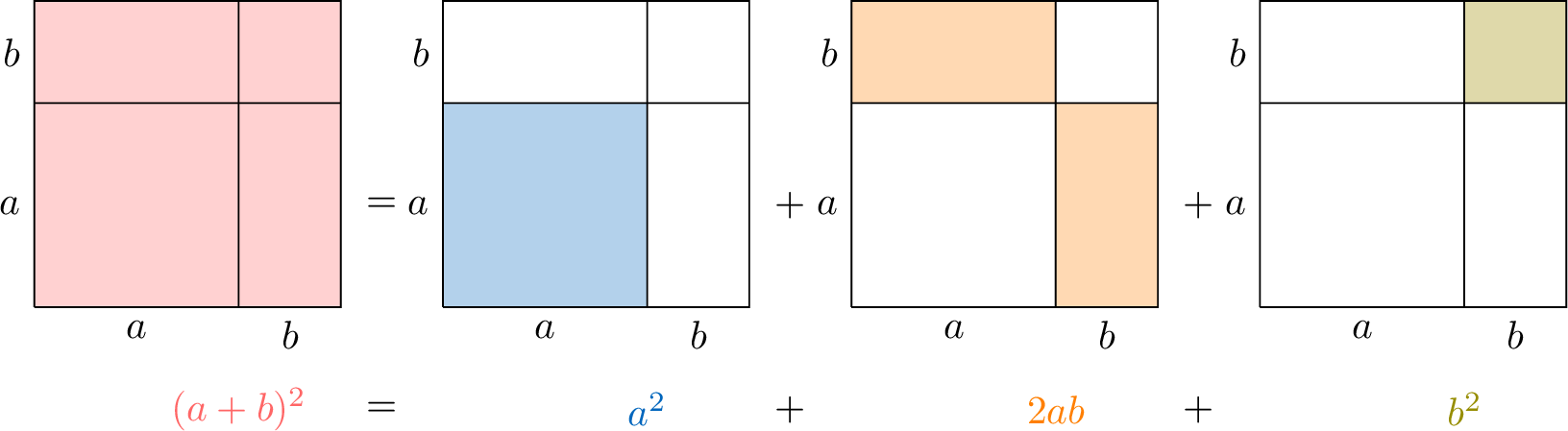
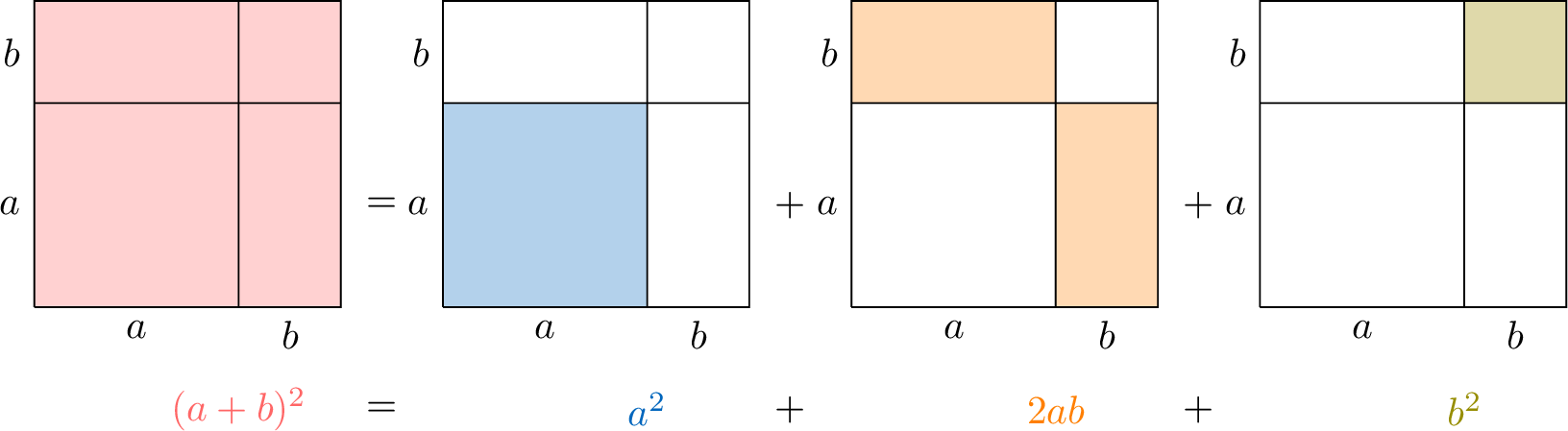
$$\begin{aligned}(a+b)^2 &= (a+b)(a+b) &&\text{(definition of a square)} \\
&= a(a+b)+b(a+b) &&\text{(distributive law)} \\
&= a^2+ab+ab+b^2 &&\text{(expanding)} \\
&= a^2+2ab+b^2 &&\text{(combining like terms)}.\end{aligned}$$Similarly,$$\begin{aligned}(a-b)^2 &= (a-b)(a-b) &&\text{(definition of a square)} \\
&= a(a-b)-b(a-b) &&\text{(distributive law)} \\
&= a^2-ab-ab+b^2 &&\text{(expanding)} \\
&= a^2-2ab+b^2 &&\text{(combining like terms)}.\end{aligned}$$
Example
Expand and simplify \((x+2)^2\).
Using the formula \((a+b)^2=a^2+2ab+b^2\) with \(a=x\) and \(b=2\):$$\begin{aligned}(\textcolor{colordef}{x}+\textcolor{colorprop}{2})^{2} &=\textcolor{colordef}{x}^{2}+2 \times \textcolor{colordef}{x} \times \textcolor{colorprop}{2}+\textcolor{colorprop}{2}^{2} \\
&=x^{2}+4 x+4.\end{aligned}$$So \((x+2)^2=x^2+4x+4\).