Similar Triangles

Angle-Angle Similarity

Definition Similar Figures

Two geometric figures are similar if they have the same shape, possibly with different sizes. This means one is an enlargement or reduction (or even an identical copy in size) of the other. The corresponding angles are equal, and the ratios of corresponding side lengths are constant.

A simple way to prove that two triangles are similar is to use the Angle-Angle (AA) Similarity Criterion: if two angles of one triangle are equal to two angles of another triangle, then the triangles are similar.

Proposition Angle-Angle Similarity for Triangles

If two angles of one triangle are equal to two angles of another triangle, then the two triangles are similar.

Example Thales and the Great Pyramid

Thales, an ancient Greek mathematician, used similar triangles to measure the height of the Great Pyramid. He measured the pyramid's shadow and, at the same time, the shadow of a staff of a known height.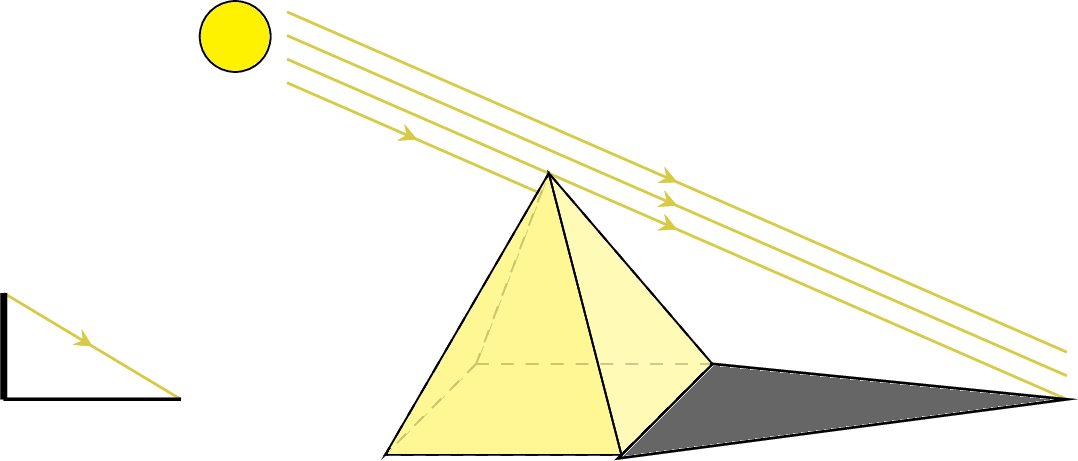

The pyramid cast a shadow 210 meters long.
A 2-meter tall staff, placed vertically, cast a shadow 3 meters long.

How can you use this information to find the height of the pyramid?

Answer

The two right triangles in the diagram (staff–shadow and pyramid–shadow) are similar by the Angle-Angle (AA) criterion:

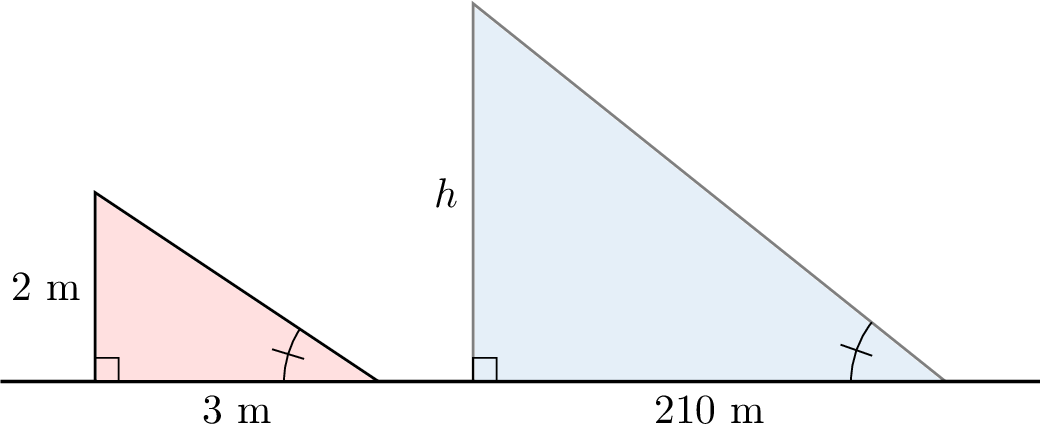
Both the staff and the pyramid form a right angle (90°) with the ground.
Because the sun's rays are parallel, the angle they make with the ground is the same for both triangles. The acute angle at the tip of each shadow is therefore equal.

Since the triangles are similar, the ratios of their corresponding sides must be equal. Let $h$ be the height of the pyramid:$$ \frac{\text{Height of Pyramid}}{\text{Shadow of Pyramid}} = \frac{\text{Height of Staff}}{\text{Shadow of Staff}} $$$$ \frac{h}{210} = \frac{2}{3} $$Solving for $h$:$$ h = 210 \times \frac{2}{3} = \frac{420}{3} = 140 $$The height of the Great Pyramid is $140$ meters.

Thales’s Theorem

Theorem Thales’s Theorem

Let $\textcolor{colordef}{\triangle ABC}$ be a triangle, with a point $\textcolor{colorprop}{D}$ on the line $\Line{A\textcolor{colordef}{B}}$ and a point $\textcolor{colorprop}{E}$ on the line $\Line{A\textcolor{colordef}{C}}$.
If the line $\textcolor{colorprop}{\Line{DE}}$ is parallel to the line $\textcolor{colordef}{\Line{BC}}$, then the triangles $\textcolor{colordef}{\triangle ABC}$ and $\textcolor{colorprop}{\triangle ADE}$ are similar:$$\dfrac{A\textcolor{colorprop}{D}}{A\textcolor{colordef}{B}} = \dfrac{A\textcolor{colorprop}{E}}{A\textcolor{colordef}{C}} = \dfrac{\textcolor{colorprop}{DE}}{\textcolor{colordef}{BC}}$$Thales’s Configurations: Key Figures

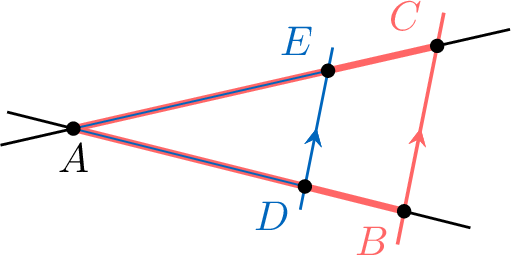
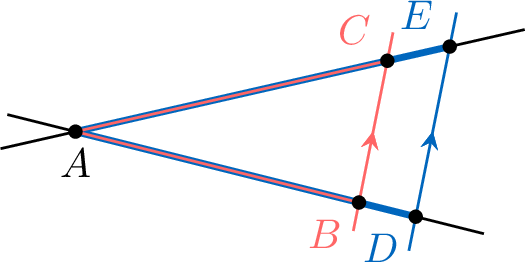
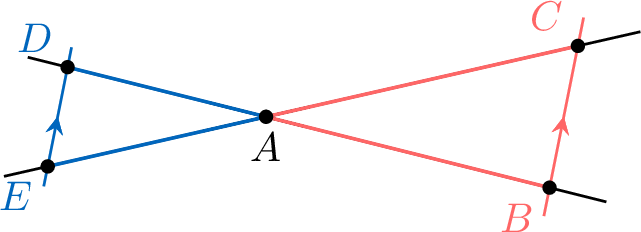
Each red triangle is similar to the blue triangle.

Proof

Since line $\textcolor{colorprop}{\Line{DE}}$ is parallel to line $\textcolor{colordef}{\Line{BC}}$, the corresponding angles are equal: $\angle ADE = \angle ABC$ and $\angle AED = \angle ACB$ (they are corresponding or alternate interior angles).
Since two angles are equal, the triangles $\textcolor{colordef}{\triangle ABC}$ and $\textcolor{colorprop}{\triangle ADE}$ are similar by the Angle-Angle (AA) criterion.
Therefore, the ratios of their corresponding sides are equal:$$\dfrac{A\textcolor{colorprop}{D}}{A\textcolor{colordef}{B}} = \dfrac{A\textcolor{colorprop}{E}}{A\textcolor{colordef}{C}} = \dfrac{\textcolor{colorprop}{DE}}{\textcolor{colordef}{BC}}$$