Exponents
Exponents are a short way to write repeated multiplication. They help us work with large numbers more easily.
Positive Exponents
Imagine you have a chessboard. You place two grains of wheat on the first square, four grains on the second square, eight grains on the third square, and so on, doubling the number of grains on each next square.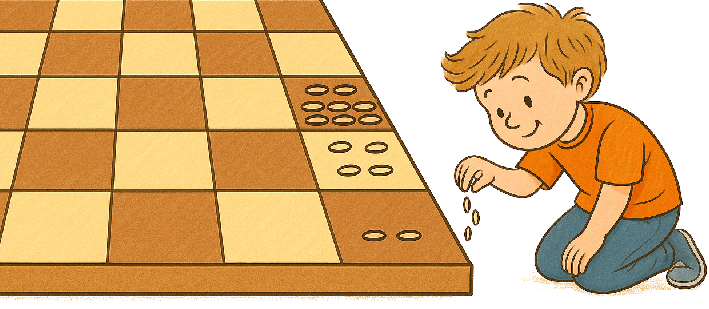
This means there are \(2^{64}\) grains on the last square. Using a calculator:$$2^{64}=18\,446\,744\,073\,709\,551\,616.$$This is an enormous number!

| Square number | Number of grains |
| \(1\) | \(2\) |
| \(2\) | \(2 \times 2\) |
| \(3\) | \(2 \times 2 \times 2\) |
| \(\vdots\) | \(\vdots\) |
| \(64\) | \(\overbrace{2 \times 2 \times \dots \times 2}^{64\ \text{factors}}\) |
This means there are \(2^{64}\) grains on the last square. Using a calculator:$$2^{64}=18\,446\,744\,073\,709\,551\,616.$$This is an enormous number!
Definition Exponentiation
Exponentiation is repeated multiplication of a number by itself.
For a number \(a\) and a positive whole number \(n\),$$a^n = \overbrace{a \times a \times \dots \times a}^{n\ \text{factors}}.$$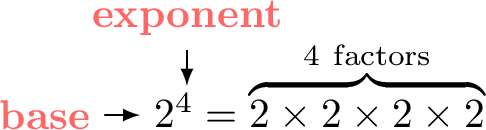
For a number \(a\) and a positive whole number \(n\),$$a^n = \overbrace{a \times a \times \dots \times a}^{n\ \text{factors}}.$$
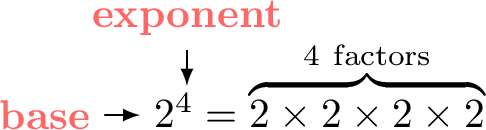
Example
Write using exponent notation: \(5 \times 5 \times 5\).
\(5 \times 5 \times 5 = 5^3\)
Definition Vocabulary
$$\begin{array}{|c|c|c|c|}\hline\text{Value} & \text{Expanded form} & \text{Exponent notation} & \text{Spoken form} \\
\hline2 & 2 & 2^1 & 2\ \text{or}\ 2\ \text{to the power of}\ 1 \\
4 & 2 \times 2 & 2^2 & 2\ \text{squared or}\ 2\ \text{to the power of}\ 2 \\
8 & 2 \times 2 \times 2 & 2^3 & 2\ \text{cubed or}\ 2\ \text{to the power of}\ 3 \\
16 & 2 \times 2 \times 2 \times 2 & 2^4 & 2\ \text{to the power of}\ 4 \\
32 & 2 \times 2 \times 2 \times 2 \times 2 & 2^5 & 2\ \text{to the power of}\ 5 \\
\hline\end{array}$$
Example
Find the value of \(2^3\).
$$\begin{aligned}[t]2^3 &= 2 \times 2 \times 2 \\
&= 8\end{aligned}$$
Negative Exponents
To understand negative exponents, let's explore the pattern of multiplying by \(2\):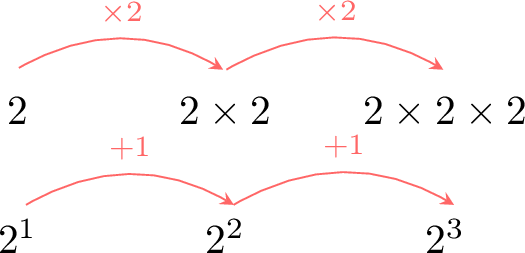


- \(2^1 = 2\)
- \(2^2 = 2 \times 2\)
- \(2^3 = 2 \times 2 \times 2\)

- \(2^0 = 1\)
- \(2^{-1} = \dfrac{1}{2}\)
- \(2^{-2} = \dfrac{1}{2 \times 2}\)
- \(2^{-3} = \dfrac{1}{2 \times 2 \times 2}\)
Definition Exponentiation for a negative exponent
For a non-zero number \(a\) and a positive integer \(n\), we extend exponentiation to negative exponents by:$$\begin{aligned}[t]a^{-n} &= \dfrac{1}{\underbrace{a \times a \times \dots \times a}_{n\ \text{factors}}} \\
&= \dfrac{1}{a^n}\end{aligned} \qquad \text{and} \qquad a^0 = 1 \quad (a \neq 0).$$In particular, \(a^{-1} = \dfrac{1}{a}\). A negative exponent means we take the reciprocal of the corresponding positive power.
Example
Write \(3^{-2}\) as a fraction.
$$\begin{aligned}[t]3^{-2} &= \dfrac{1}{3 \times 3} \\
&= \dfrac{1}{9}\end{aligned}$$
Exponent Law 1
$$\begin{aligned}\textcolor{colordef}{7}^{\textcolor{colorprop}{3}} \times \textcolor{colordef}{7}^{\textcolor{olive}{2}}&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}\,\text{factors}} \times \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{olive}{2}\,\text{factors}} \\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}\,\text{factors}} \\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and multiplied by the same number raised to the power \(\textcolor{olive}{n}\), that is$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}},$$the result is equal to \(\textcolor{colordef}{a}\) raised to the sum of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}.$$
Proposition Exponent Law 1
For \(a\neq 0\) and any numbers \(m\) and \(n\),$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}$$
$$\begin{aligned}\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}\ \text{factors}} \times \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{olive}{n}\ \text{factors}} \\
&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}\ \text{factors}} \\
&= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}\end{aligned}$$
Example
Simplify \(5^2\times 5^4\).
$$\begin{aligned}\textcolor{colordef}{5}^{\textcolor{colorprop}{2}} \times \textcolor{colordef}{5}^{\textcolor{olive}{4}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2}+\textcolor{olive}{4}} && \text{(same base, add exponents)} \\
&= \textcolor{colordef}{5}^{6}.\end{aligned}$$
Exponent Law 2
Let's look at an example:$$\begin{aligned}\dfrac{\textcolor{colordef}{7}^{\textcolor{colorprop}{5}}}{\textcolor{colordef}{7}^{\textcolor{olive}{2}}}&= \dfrac{\overbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5}\,\text{factors}}} {\underbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}}}_{\textcolor{olive}{2}\,\text{factors}}}\\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}\,\text{factors}}\\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and divided by the same number raised to the power \(\textcolor{olive}{n}\), that is$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}},$$the result is \(\textcolor{colordef}{a}\) raised to the difference of the exponents:$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}.$$
Proposition Exponent Law 2
For \(a\neq 0\) and any numbers \(m\) and \(n\),$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}$$
Example
Simplify \(\dfrac{5^7}{5^3}\).
$$\begin{aligned}\dfrac{\textcolor{colordef}{5}^{\textcolor{colorprop}{7}}}{\textcolor{colordef}{5}^{\textcolor{olive}{3}}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{7} - \textcolor{olive}{3}} \\
&= \textcolor{colordef}{5}^{4}\end{aligned}$$
Exponent Law 3
Let's look at an example:$$\begin{aligned}\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{3}}&= (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})^{\textcolor{olive}{3}} \\
&= \overbrace{(\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})}^{\textcolor{olive}{3}\,\text{factors}} \\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} + \textcolor{colorprop}{2} +\textcolor{colorprop}{2}}\\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{3}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\), and that result is raised to the power \(\textcolor{olive}{n}\), that is$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}},$$the result is \(\textcolor{colordef}{a}\) raised to the product of the exponents:$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}.$$
Proposition Exponent Law 3
For \(a\neq 0\) and any numbers \(m\) and \(n\),$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}$$
Example
Simplify \(\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}}\).
$$\begin{aligned}[t]\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{5}} \\
&= \textcolor{colordef}{5}^{10}\end{aligned}$$
Exponent Law 4
Let's look at an example:$$\begin{aligned}(\textcolor{colordef}{3} \times \textcolor{colorprop}{5})^{\textcolor{olive}{2}}&= (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \times (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \times \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \\
&= (\textcolor{colordef}{3} \times \textcolor{colordef}{3}) \times (\textcolor{colorprop}{5} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3}^{\textcolor{olive}{2}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{2}}\end{aligned}$$In general, when you multiply two numbers \(\textcolor{colordef}{a}\) and \(\textcolor{colorprop}{b}\), and then raise the product to the power \(\textcolor{olive}{n}\), that is$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}},$$the result is each factor raised to the power \(\textcolor{olive}{n}\):$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}.$$
Proposition Exponent Law 4
For any numbers \(n\) and any numbers \(a\) and \(b\),$$\left(\textcolor{colordef}{a}\textcolor{colorprop}{b}\right)^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}$$
Example
Simplify \((\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}}\).
$$(\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}}= \textcolor{colordef}{2}^{\textcolor{olive}{3}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{3}}$$
Exponent Law 5
Let's look at an example:$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \times \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \\
&= \dfrac{\textcolor{colordef}{5} \times \textcolor{colordef}{5}}{\textcolor{colorprop}{3} \times \textcolor{colorprop}{3}} \\
&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}\end{aligned}$$In general, when a quotient \(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\) is raised to a power \(\textcolor{olive}{n}\), that is$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}},$$the result is the numerator raised to that power divided by the denominator raised to that power:$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}}= \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}.$$
Proposition Exponent Law 5
For \(b\neq 0\) and any number \(n\),$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}}= \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}$$
Example
Calculate \(\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}\).
$$\begin{aligned}[t]\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}} \\
&= \dfrac{25}{9}\end{aligned}$$
Order of operations
The order of operations is a set of rules that tells us which calculations to do first in a mathematical expression.
Definition Order of Operations
To solve mathematical expressions accurately, we follow the order of operations, which is commonly remembered using the acronym PEMDAS:
- P: Parentheses
- E: Exponents
- M: Multiplication
- D: Division
- A: Addition
- S: Subtraction
Example
Evaluate \((1+2) \times 2^3 + 4\).
$$\begin{aligned}[t](1+2) \times 2^3 + 4 &= \textcolor{colordef}{(1+2)} \times 2^3 + 4 && (\text{parentheses: } \textcolor{colordef}{(1+2)} = 3) \\
&= 3 \times \textcolor{colordef}{2^3} + 4 && (\text{exponent: } \textcolor{colordef}{2^3} = 8) \\
&= \textcolor{colordef}{3 \times 8} + 4 && (\text{multiplication: } \textcolor{colordef}{3 \times 8} = 24) \\
&= \textcolor{colordef}{24 + 4} && (\text{addition: } \textcolor{colordef}{24 + 4} = 28) \\
&= 28\end{aligned}$$