Integers
Definition
Imagine a world with two types of particles: positives (+) and negatives (-). They interact in specific ways.
- When particles of the same type meet, they join forces.
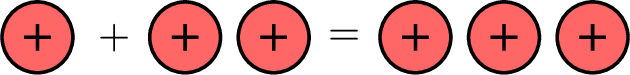
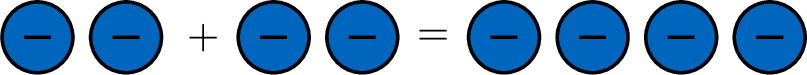
- When a positive and a negative particle meet, they cancel each other out, leaving nothing. This is called a zero pair.

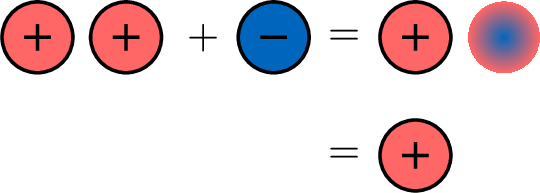
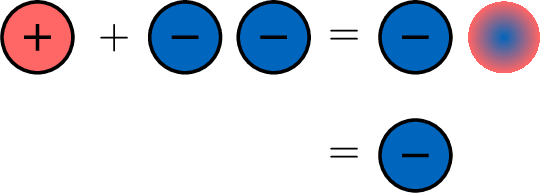
- Let’s see what happens if 2 positives meet 1 negative. One zero pair is formed, leaving 1 positive.
- To show which type of particle we have, we put a sign in front of the number:
- The + sign for a group of positives.

- The - sign for a group of negatives.

- The + sign for a group of positives.
- Now, let’s see what happens when 3 positives meet 1 negative.
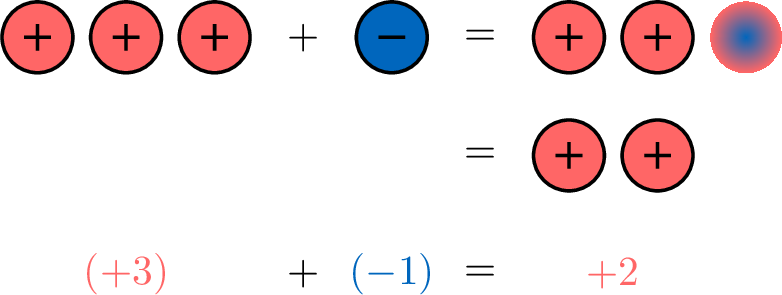
- Finally, let’s see what happens when 2 positives meet 2 negatives.
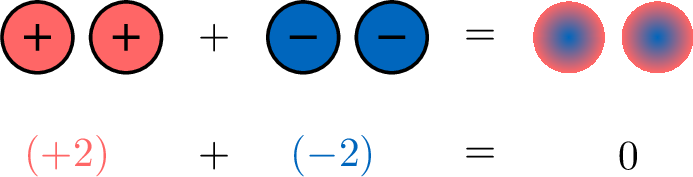
Definition Integers
The integers are the set that contains the natural numbers (\(1, 2, 3, \dots\)), their opposites (\(-1, -2, -3, \dots\)), and \(0\).
- Positive numbers (\(\textcolor{colordef}{+1}, \textcolor{colordef}{+2},\dots\)) are written with a positive sign \((+)\). This sign is often omitted (\(\textcolor{colordef}{+2}=\textcolor{colordef}{2}\)).
\(\textcolor{colordef}{+2}=\) 
- Negative numbers (\(\textcolor{colorprop}{-1}, \textcolor{colorprop}{-2},\dots\)) are written with a negative sign \((-)\).
\(\textcolor{colorprop}{-3}=\) 
- Zero (\(0\)) is neither positive nor negative.
- Two numbers are opposites if their sum is \(0\).
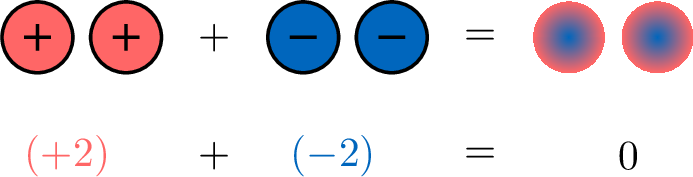
\(\textcolor{colorprop}{-2}\) is the opposite of \(\textcolor{colordef}{+2}\). - To avoid confusion between a number's sign and an operation sign, we often use parentheses. For example, \(\textcolor{colordef}{+1}+\textcolor{colorprop}{-2}\) can be written as \(\textcolor{colordef}{(+1)}+\textcolor{colorprop}{(-2)}\).
Example
Calculate \(\textcolor{colordef}{(+1)}+\textcolor{colorprop}{(-2)}\).
-
- So, \(\textcolor{colordef}{(+1)}+\textcolor{colorprop}{(-2)}=\textcolor{colorprop}{-1}\).
Definition Absolute Value
The absolute value of a number is the number without its sign.
- The absolute value of \(\textcolor{colordef}{+2}=\)
 is \(2\).
is \(2\). - The absolute value of \(\textcolor{colorprop}{-3}=\)
 is \(3\).
is \(3\).
Rules of Addition
Method Rules of Addition
- When you add two positive numbers, add their absolute values. The sum is also a positive number:$$\textcolor{colordef}{(+2)}+\textcolor{colordef}{(+4)}=\textcolor{colordef}{+6} \quad \text{as }2+4=6.$$
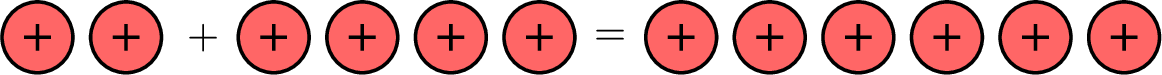
- When you add two negative numbers, add their absolute values. The sum is also a negative number:$$\textcolor{colorprop}{(-5)}+\textcolor{colorprop}{(-3)}=\textcolor{colorprop}{-8} \quad \text{as }5+3=8.$$
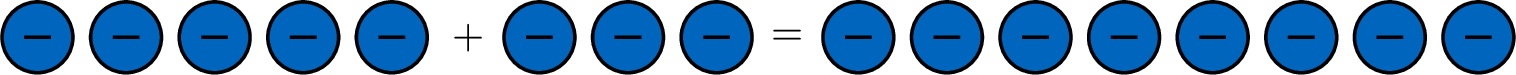
- When you add a positive number and a negative number, subtract the smaller absolute value from the larger one and use the sign of the number with the larger absolute value.
\(\textcolor{colorprop}{(-2)}+\textcolor{colordef}{(+5)}=\textcolor{colordef}{+3} \quad \text{as }5-2=3\) 
\(\textcolor{colordef}{(+2)}+\textcolor{colorprop}{(-6)}=\textcolor{colorprop}{-4} \quad \text{as }6-2=4\) 
Example
Calculate \(\textcolor{colorprop}{(-10)}+\textcolor{colordef}{(+3)}\).
- \(\textcolor{colorprop}{(-10)}+\textcolor{colordef}{(+3)}=\textcolor{colorprop}{-7} \quad \text{as }10-3=7.\)
-
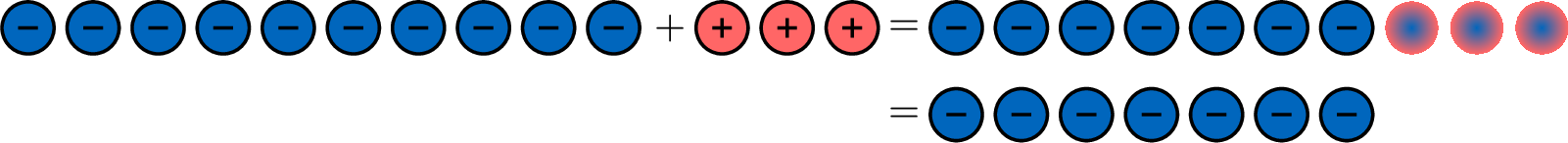
Subtraction
- For the subtraction, \(\textcolor{colordef}{(+3)}-\textcolor{colordef}{(+2)}\):
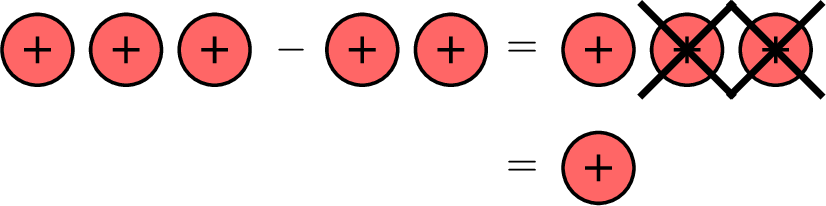
- For the addition, \(\textcolor{colordef}{(+3)}+\textcolor{colorprop}{(-2)}\):
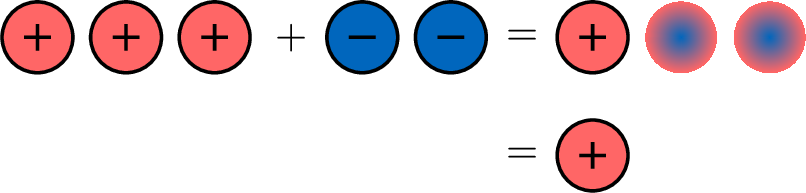
- Therefore, these two operations are equivalent:
\(\textcolor{colordef}{(+3)}-\textcolor{colordef}{(+2)}=\textcolor{colordef}{(+3)}+\textcolor{colorprop}{(-2)}\) 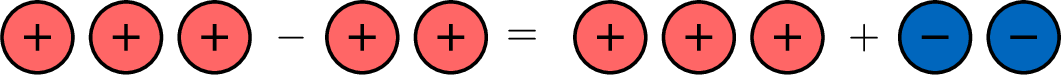
- For the subtraction, \(\textcolor{colordef}{(+3)}-\textcolor{colordef}{(+2)}\):
- For the subtraction, \(\textcolor{colorprop}{(-3)}-\textcolor{colorprop}{(-2)}\):
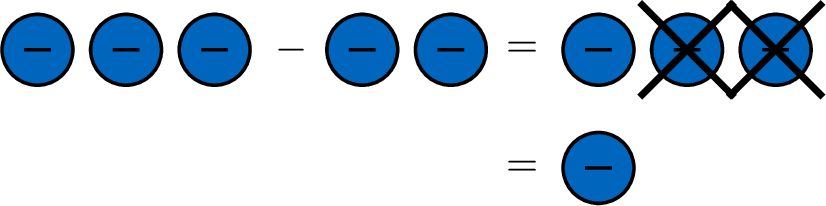
- For the addition, \(\textcolor{colorprop}{(-3)}+\textcolor{colordef}{(+2)}\):
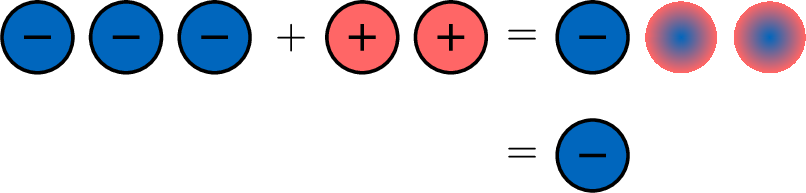
- Therefore, these two operations are equivalent:
\(\textcolor{colorprop}{(-3)}-\textcolor{colorprop}{(-2)}=\textcolor{colorprop}{(-3)}+\textcolor{colordef}{(+2)}\) 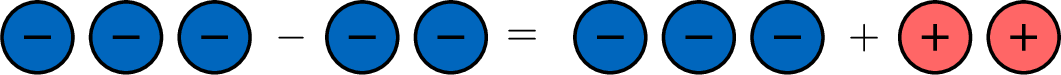
- For the subtraction, \(\textcolor{colorprop}{(-3)}-\textcolor{colorprop}{(-2)}\):
- In conclusion, these examples show a fundamental rule in arithmetic: subtracting any number is equivalent to adding the number with its opposite sign.
Definition Subtraction
Subtracting a number means adding its opposite.
Example
Calculate \(\textcolor{colordef}{(+4)}-\textcolor{colorprop}{(-2)}\).
$$\begin{aligned}[t]\textcolor{colordef}{(+4)}-\textcolor{colorprop}{(-2)}&=\textcolor{colordef}{(+4)}+\textcolor{colordef}{(+2)}&&\text{(add the opposite)}\\
&=\textcolor{colordef}{+6}&&\text{(same sign: add the absolute values)}\end{aligned}$$

On the Number Line
- To show both positive and negative numbers on a number line, we extend the number line in both directions from zero.
- For each move from left to right by \(1\), the number increases by \(1\): \(0+1=\textcolor{colordef}{+1}\), \(\textcolor{colordef}{+1}+1=\textcolor{colordef}{+2},\dots\)
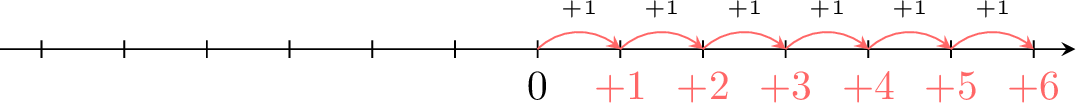
- For each move from right to left by \(1\), the number decreases by \(1\): \(0-1=\textcolor{colorprop}{-1}\), \(\textcolor{colorprop}{-1}-1=\textcolor{colorprop}{-2},\dots\)
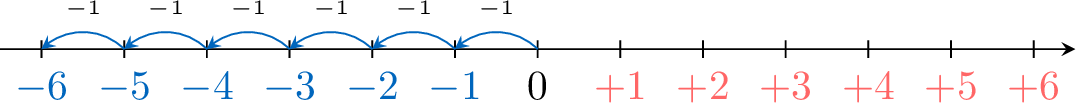
Definition Number line
A number line is a straight line with markings at equal intervals to denote the numbers.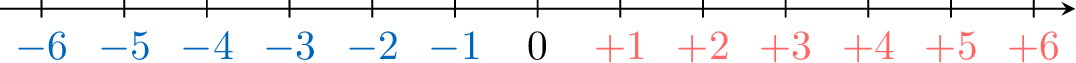
Example
Find the value of \(x\).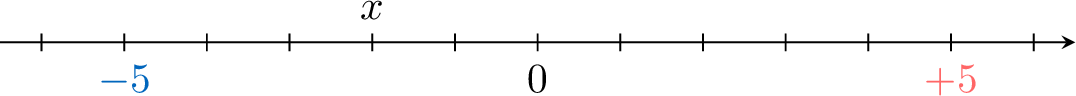
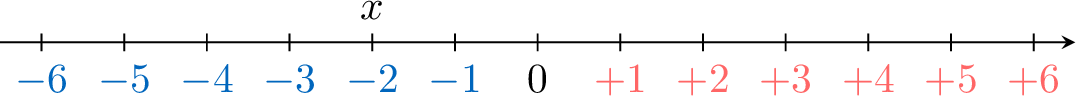
- So, \(x=\textcolor{colorprop}{-2}\).
Ordering
In the set of integers, the order is defined as:$$\dots\lt\textcolor{colorprop}{-3}\lt\textcolor{colorprop}{-2}\lt\textcolor{colorprop}{-1}\lt 0 \lt \textcolor{colordef}{+1}\lt\textcolor{colordef}{+2}\lt\textcolor{colordef}{+3}\lt\dots $$So, as you move along the number line from left to right, the numbers increase.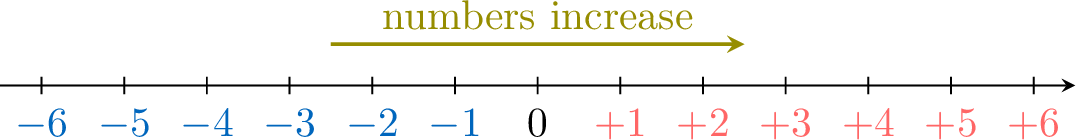
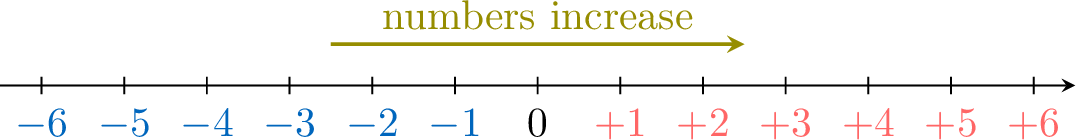
- As \(\textcolor{colordef}{+3}\) is to the right of \(\textcolor{colorprop}{-5}\), \(\textcolor{colorprop}{-5} \lt \textcolor{colordef}{+3}\). So, when one number is positive and the other is negative, the positive number is greater.
- As \(\textcolor{colorprop}{-2}\) is to the right of \(\textcolor{colorprop}{-4}\), \(\textcolor{colorprop}{-4}\lt \textcolor{colorprop}{-2}\). So, when both numbers are negative, the number closer to zero is greater (the number with the smaller absolute value is greater).
- As \(\textcolor{colordef}{+6}\) is to the right of \(\textcolor{colordef}{+4}\), \(\textcolor{colordef}{+4}\lt \textcolor{colordef}{+6}\). So, when both numbers are positive, the number further from zero is greater (the number with the greater absolute value is greater).
Method Compare two numbers
- When one number is positive and the other is negative, the positive number is greater.
- When both numbers are negative, the number closer to zero is greater (the number with the smaller absolute value is greater).
- When both numbers are positive, the number further from zero is greater (the number with the greater absolute value is greater).
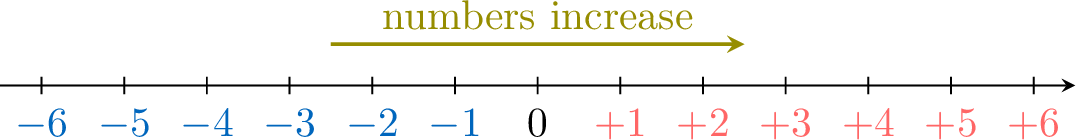
Example
Compare \(\textcolor{colorprop}{-4}\) and \(\textcolor{colordef}{+3}\).
- As \(\textcolor{colordef}{+3}\) is positive and \(\textcolor{colorprop}{-4}\) is negative, the positive number is greater than the negative number: \(\textcolor{colorprop}{-4}\lt \textcolor{colordef}{+3}\).
-
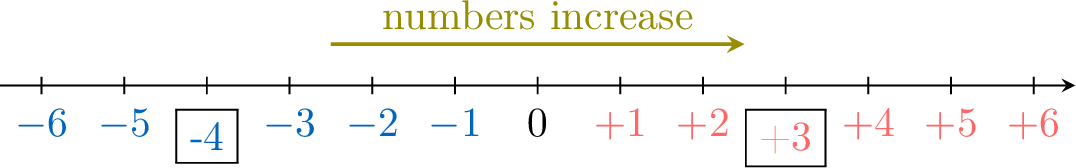
Multiplication
Multiplication of two whole numbers can be seen as repeated addition: \(3\times 2=2+2+2=6\).
We now extend this idea to signed numbers:
We now extend this idea to signed numbers:
- \(\textcolor{colordef}{(+)}\times \textcolor{colordef}{(+)}\):$$\begin{aligned}[t]\textcolor{colordef}{(+3)}\times \textcolor{colordef}{(+2)}&=3\times \textcolor{colordef}{(+2)}\\
&=\textcolor{colordef}{(+2)} + \textcolor{colordef}{(+2)} + \textcolor{colordef}{(+2)}\\
&=\textcolor{colordef}{+6}\end{aligned}$$
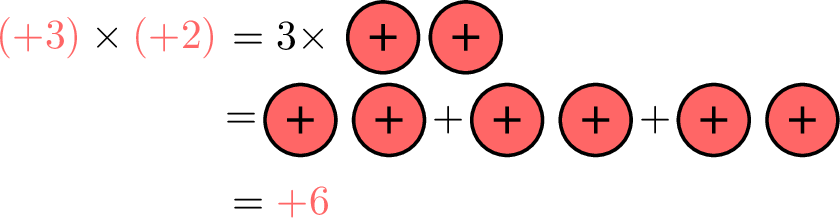
- \(\textcolor{colordef}{(+)}\times \textcolor{colorprop}{(-)}\):$$\begin{aligned}[t]\textcolor{colordef}{(+3)}\times \textcolor{colorprop}{(-2)}&=3\times \textcolor{colorprop}{(-2)}\\
&=\textcolor{colorprop}{(-2)} + \textcolor{colorprop}{(-2)} + \textcolor{colorprop}{(-2)}\\
&=\textcolor{colorprop}{-6}\end{aligned}$$
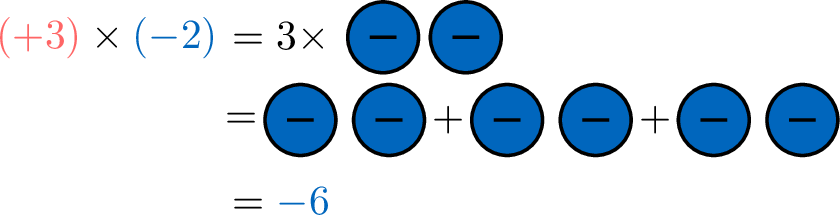
- \(\textcolor{colorprop}{(-)} \times \textcolor{colordef}{(+)}\): Multiplication is commutative, so the order does not matter.$$\begin{aligned}[t]\textcolor{colorprop}{(-2)} \times \textcolor{colordef}{(+3)} &=\textcolor{colordef}{(+3)}\times \textcolor{colorprop}{(-2)}\\ &=\textcolor{colorprop}{-6}\end{aligned}$$So, a negative times a positive gives a negative.
- \(\textcolor{colorprop}{(-)} \times \textcolor{colorprop}{(-)}\):We know that \(0\times \textcolor{colorprop}{(-2)}=0\). Also,\(0=\textcolor{colordef}{(+3)} + \textcolor{colorprop}{(-3)}\), so:$$\begin{aligned}[t](\textcolor{colordef}{(+3)} + \textcolor{colorprop}{(-3)})\times \textcolor{colorprop}{(-2)} &= 0\\ \textcolor{colordef}{(+3)}\times\textcolor{colorprop}{(-2)} + \textcolor{colorprop}{(-3)}\times\textcolor{colorprop}{(-2)} &= 0\\ \textcolor{colorprop}{-6} + \big(\textcolor{colorprop}{(-3)}\times\textcolor{colorprop}{(-2)}\big) &= 0\\ \textcolor{colorprop}{(-3)}\times \textcolor{colorprop}{(-2)}&=\textcolor{colordef}{+6}\end{aligned}$$So, a negative times a negative gives a positive.
Definition Multiplication
The product of two signed integers is obtained by:
- multiplying their absolute values;
- then deciding the sign using the following rules:
- \(\textcolor{colordef}{(+)}\times \textcolor{colordef}{(+)} = \textcolor{colordef}{(+)}\): a positive times a positive gives a positive.
- \(\textcolor{colordef}{(+)}\times \textcolor{colorprop}{(-)} = \textcolor{colorprop}{(-)}\): a positive times a negative gives a negative.
- \(\textcolor{colorprop}{(-)} \times \textcolor{colordef}{(+)} = \textcolor{colorprop}{(-)}\): a negative times a positive gives a negative.
- \(\textcolor{colorprop}{(-)} \times \textcolor{colorprop}{(-)} = \textcolor{colordef}{(+)}\): a negative times a negative gives a positive.
Example
Calculate \(\textcolor{colordef}{(+2)}\times \textcolor{colorprop}{(-5)}\).
$$\textcolor{colordef}{(+2)}\times \textcolor{colorprop}{(-5)}= \textcolor{colorprop}{-10}\quad (2\times 5 = 10 \text{ and } \textcolor{colordef}{(+)}\times \textcolor{colorprop}{(-)} = \textcolor{colorprop}{(-)})$$
Division
Multiplication and division are inverse operations:$$\textcolor{black}{3}\times \textcolor{black}{2}=\textcolor{black}{6}, \text{ so }\textcolor{black}{6}\div \textcolor{black}{3}=\textcolor{black}{2}.$$(Here we only divide by non-zero numbers.)
Now, let's look at division with negative numbers:
Now, let's look at division with negative numbers:
- \(\textcolor{colordef}{(+)} \div \textcolor{colordef}{(+)}\):$$\textcolor{colordef}{(+3)} \times \textcolor{colordef}{(+2)}=\textcolor{colordef}{+6}, \text{ so }\textcolor{colordef}{(+6)} \div \textcolor{colordef}{(+3)}=\textcolor{colordef}{(+2)}.$$So, a positive divided by a positive gives a positive.
- \(\textcolor{colordef}{(+)} \div \textcolor{colorprop}{(-)}\):$$\textcolor{colorprop}{(-3)} \times \textcolor{colorprop}{(-2)}=\textcolor{colordef}{+6}, \text{ so }\textcolor{colordef}{(+6)} \div \textcolor{colorprop}{(-3)}=\textcolor{colorprop}{(-2)}.$$So, a positive divided by a negative gives a negative.
- \(\textcolor{colorprop}{(-)} \div \textcolor{colordef}{(+)}\):$$\textcolor{colordef}{(+3)} \times \textcolor{colorprop}{(-2)}=\textcolor{colorprop}{-6}, \text{ so }\textcolor{colorprop}{(-6)} \div \textcolor{colordef}{(+3)}=\textcolor{colorprop}{(-2)}.$$So, a negative divided by a positive gives a negative.
- \(\textcolor{colorprop}{(-)} \div \textcolor{colorprop}{(-)}\):$$\textcolor{colorprop}{(-3)} \times \textcolor{colordef}{(+2)}=\textcolor{colorprop}{-6}, \text{ so }\textcolor{colorprop}{(-6)} \div \textcolor{colorprop}{(-3)}=\textcolor{colordef}{(+2)}.$$So, a negative divided by a negative gives a positive.
Definition Division
The quotient of two integers (with a non-zero divisor) is obtained by:
- dividing their absolute values;
- then deciding the sign using the following rules:
- \(\textcolor{colordef}{(+)}\div \textcolor{colordef}{(+)} = \textcolor{colordef}{(+)}\): a positive divided by a positive gives a positive.
- \(\textcolor{colordef}{(+)}\div \textcolor{colorprop}{(-)} = \textcolor{colorprop}{(-)}\): a positive divided by a negative gives a negative.
- \(\textcolor{colorprop}{(-)} \div \textcolor{colordef}{(+)} = \textcolor{colorprop}{(-)}\): a negative divided by a positive gives a negative.
- \(\textcolor{colorprop}{(-)} \div \textcolor{colorprop}{(-)} = \textcolor{colordef}{(+)}\): a negative divided by a negative gives a positive.
Example
Calculate \(\textcolor{colordef}{(+10)}\div \textcolor{colorprop}{(-5)}\).
$$\textcolor{colordef}{(+10)}\div \textcolor{colorprop}{(-5)}= \textcolor{colorprop}{-2} \quad (10\div 5 = 2 \text{ and } \textcolor{colordef}{(+)}\div \textcolor{colorprop}{(-)} = \textcolor{colorprop}{(-)})$$