Relationships between Angles

In this chapter, we will explore relationships between angles that are key to solving geometry problems. You will learn about complementary angles (summing to $90^\circ$, forming a right angle), supplementary angles (summing to $180^\circ$, forming a straight angle), opposite angles at a vertex (formed by intersecting lines), and angles created by parallel lines and a transversal, including corresponding, alternate, and co-interior angles. These concepts build on your understanding of right angles ($90^\circ$), straight angles ($180^\circ$), and full angles ($360^\circ$).

Complementary and Supplementary Angles

Definition Complementary

Two angles are complementary if their sum is $90^\circ$. Complementary angles together form a right angle, like the corner of a square.

Example

Calculate the measure of the unknown angle $x^\circ$ if it is complementary to a $35^\circ$ angle.

Answer

The sum of complementary angles is $90^\circ$.$$\begin{aligned}x^\circ + 35^\circ &= 90^\circ \\x^\circ &= 90^\circ - 35^\circ \quad (\text{subtract } 35^\circ) \\&= 55^\circ\end{aligned}$$

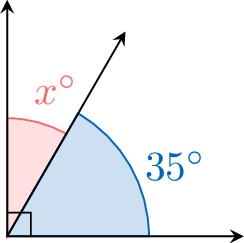
Definition Supplementary

Two angles are supplementary if their sum is $180^\circ$. Supplementary angles together form a straight line.

Example

Calculate the measure of the unknown angle $x^\circ$ if it is supplementary to a $110^\circ$ angle.

Answer

The sum of supplementary angles is $180^\circ$.$$\begin{aligned}x^\circ + 110^\circ &= 180^\circ \\x^\circ &= 180^\circ - 110^\circ \quad (\text{subtract } 110^\circ) \\&= 70^\circ\end{aligned}$$

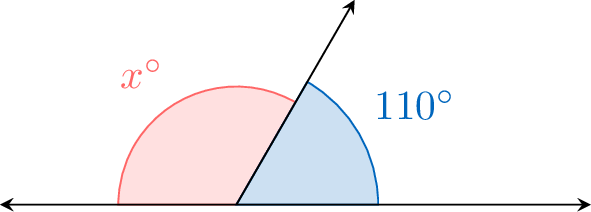
Opposite Angles at a Vertex

Definition Opposite Angles at a Vertex

Opposite angles at a vertex are angles that are opposite each other at the point where two lines intersect, sharing a common vertex.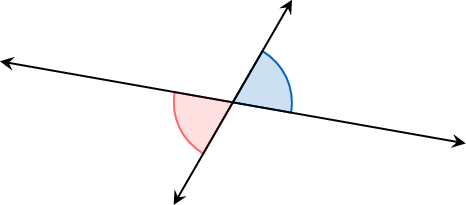

Proposition Equality of Opposite Angles at a Vertex

Opposite angles at a vertex are equal.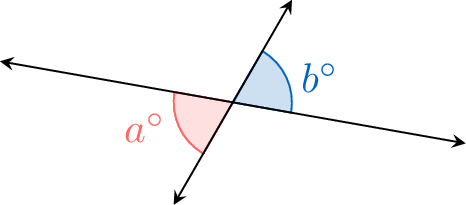

$\textcolor{colordef}{a^\circ} = \textcolor{colorprop}{b^\circ}$

Proof

Consider two lines intersecting at a point, forming opposite angles $a^\circ$ and $b^\circ$, and an adjacent angle $c^\circ$.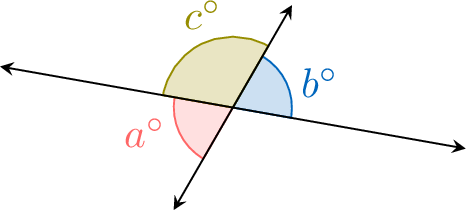

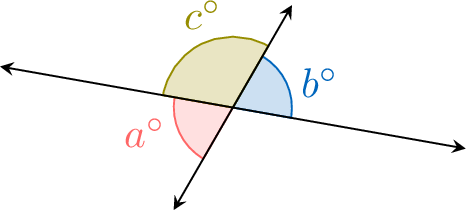
Since $a^\circ$ and $c^\circ$ form a straight angle:$$\textcolor{colordef}{a^\circ} + \textcolor{olive}{c^\circ} = 180^\circ \quad (\text{straight angle})$$Similarly, $b^\circ$ and $c^\circ$ form a straight angle:$$\textcolor{colorprop}{b^\circ} + \textcolor{olive}{c^\circ} = 180^\circ \quad (\text{straight angle})$$Thus, $\textcolor{colordef}{a^\circ} + \textcolor{olive}{c^\circ} = \textcolor{colorprop}{b^\circ} + \textcolor{olive}{c^\circ}$. Subtracting $\textcolor{olive}{c^\circ}$ from both sides gives:$$\textcolor{colordef}{a^\circ} = \textcolor{colorprop}{b^\circ}$$

Example

Calculate the measure of the unknown angle $x^\circ$.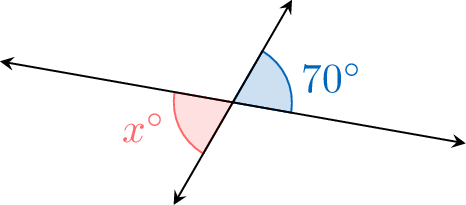

Answer

Opposite angles at a vertex are equal.$$\begin{aligned}x^\circ &= 70^\circ \quad (\text{opposite angles are equal})\end{aligned}$$

Corresponding, Alternate, and Co-interior Angles

Definition Corresponding, Alternate, and Co-interior Angles

Corresponding angles are on the same side of a transversal that intersects two lines and are in matching corners relative to the intersected lines, like the top-right corners of each intersection.
Alternate angles are on opposite sides of a transversal and lie between the two intersected lines, forming a "Z" shape.
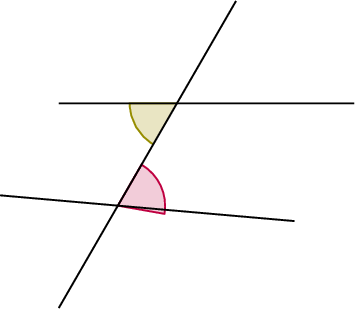
Co-interior angles are on the same side of a transversal and between the two intersected lines, forming a "C" shape.

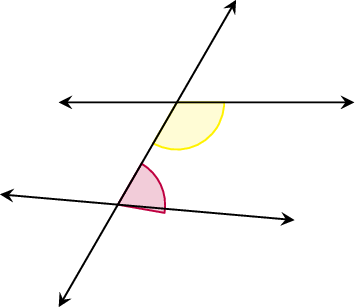
Example

Identify the following for the given diagram: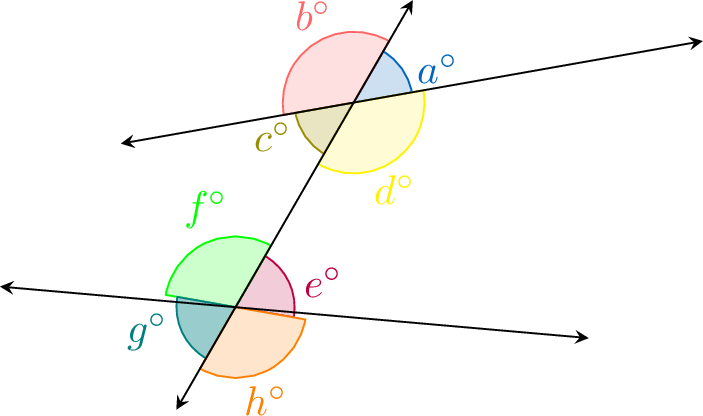

The corresponding angles.
The alternate angles.
The co-interior angles.

Answer

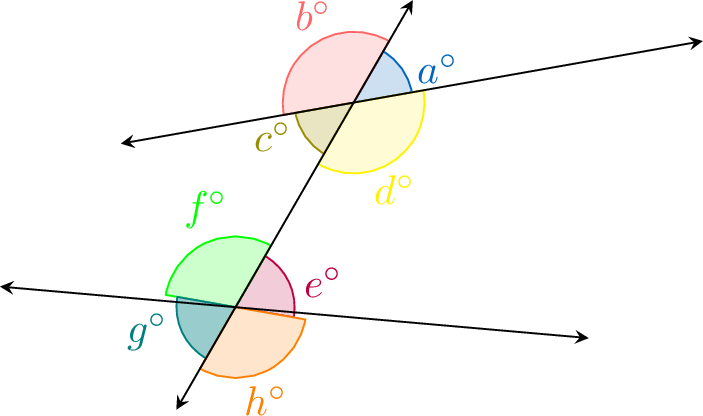
Corresponding angles: $\textcolor{colorprop}{a^\circ}$ and $\textcolor{purple}{e^\circ}$, $\textcolor{colordef}{b^\circ}$ and $\textcolor{green}{f^\circ}$, $\textcolor{olive}{c^\circ}$ and $\textcolor{teal}{g^\circ}$, $\textcolor{yellow}{d^\circ}$ and $\textcolor{orange}{h^\circ}$.
Alternate angles: $\textcolor{olive}{c^\circ}$ and $\textcolor{purple}{e^\circ}$, $\textcolor{yellow}{d^\circ}$ and $\textcolor{green}{f^\circ}$.
Co-interior angles: $\textcolor{olive}{c^\circ}$ and $\textcolor{green}{f^\circ}$, $\textcolor{yellow}{d^\circ}$ and $\textcolor{purple}{e^\circ}$.

Properties of Parallel Lines

Proposition Properties of Parallel Lines

If two lines are parallel and intersected by a transversal, then: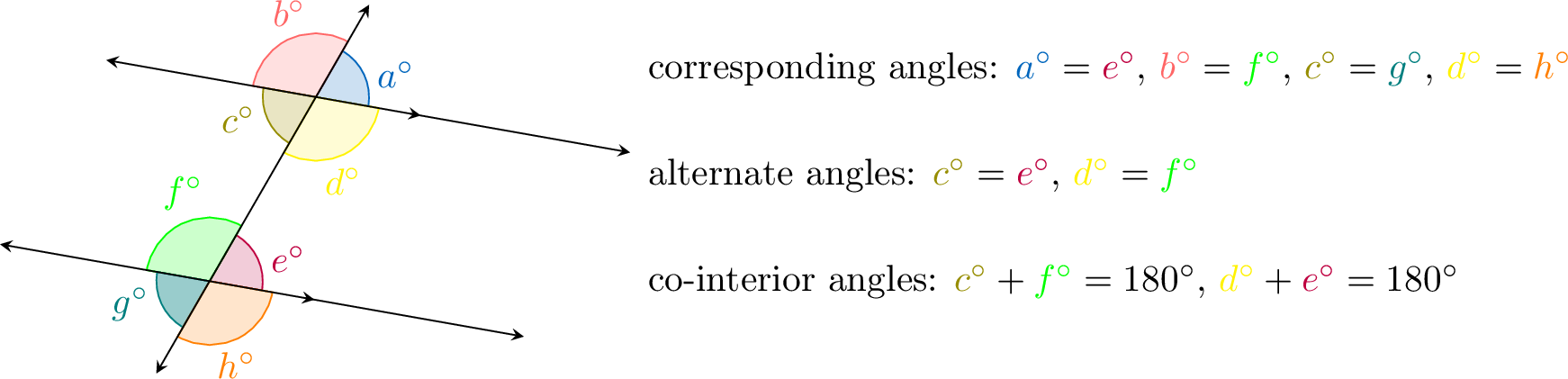

Corresponding angles are equal.
Alternate angles are equal.
Co-interior angles are supplementary (sum to $180^\circ$).

Example

Calculate the measure of the unknown angle $x^\circ$, given that the lines are parallel.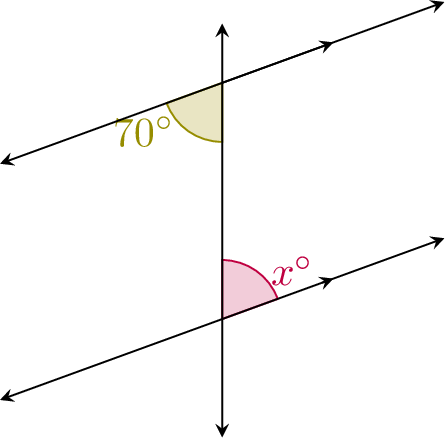

Answer

Since the angles are alternate and the lines are parallel, they are equal.$$\begin{aligned}x^\circ &= 70^\circ \quad (\text{alternate angles are equal})\end{aligned}$$

Proposition Parallel Lines from Equal Angles

If any pair of corresponding angles or alternate angles are equal, then the lines are parallel.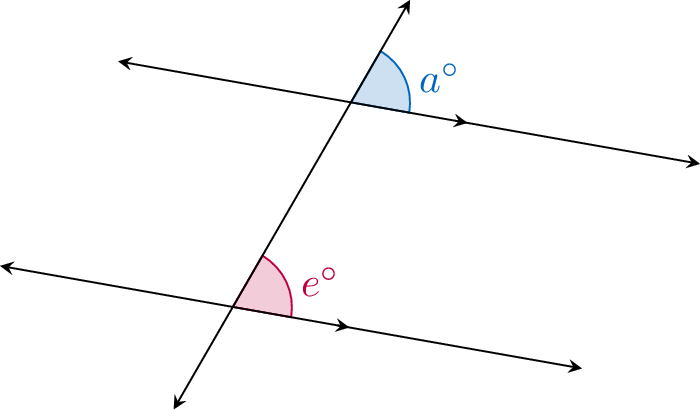

Example

Show that the lines are parallel, given the angle measures.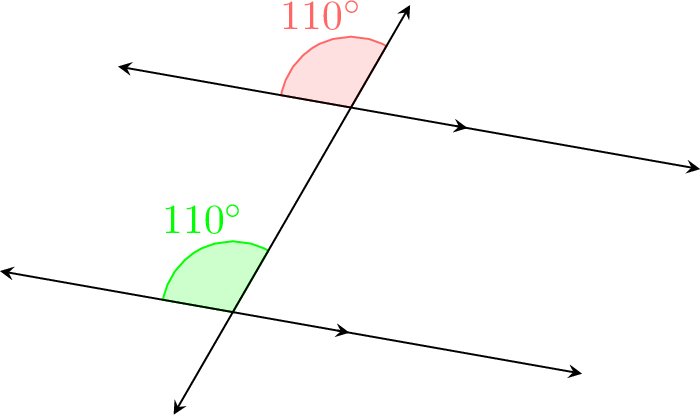

Answer

Since the corresponding angles are equal ($110^\circ = 110^\circ$), the lines are parallel.