Angles
Angles are a fundamental concept in geometry. They are formed when two rays meet at a single point, called the vertex.
Definition
Definition Angle
An angle is the measure of rotation between two rays that share a common endpoint, called the vertex.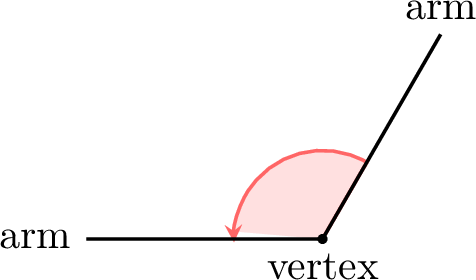

Degrees
A full turn, or complete circle, is divided into 360 equal parts called degrees, a convention established by ancient Babylonian astronomers.
Definition Degree Unit
A degree is a unit of angle measurement. A full turn measures \(360^\circ\).

Definition Measure of an Angle in Degrees
The measure of an angle in degrees is the fraction of a full turn it represents.
Example
Calculate the measure of an angle that represents one-third of a full turn.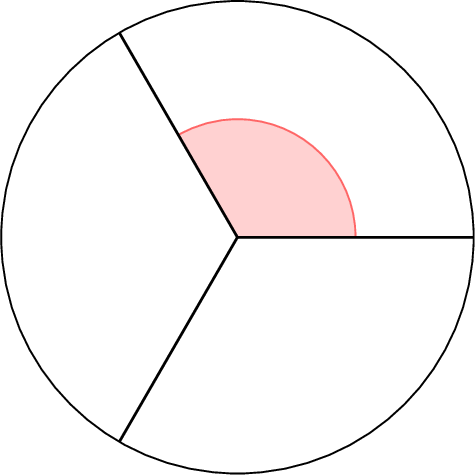

$$\begin{aligned}\text{Angle} &= \frac{1}{3} \text{ of } 360^\circ \\&= 360^\circ \div 3 \\&= 120^\circ\end{aligned}$$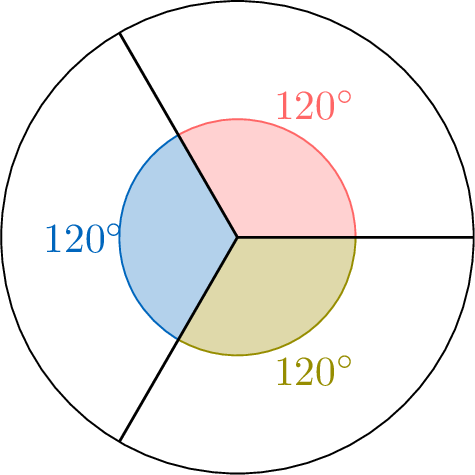

Measuring and Drawing Angles with a Protractor
Definition Protractor
A protractor is a tool used to measure and draw angles in degrees. It is typically a semi-circular tool with a scale marked from \(0^\circ\) to \(180^\circ\).

Method Measuring an Angle with a Protractor
- Place the protractor’s origin (center point) over the vertex of the angle.
- Align one ray of the angle with the protractor’s baseline (the \(0^\circ\) mark).
- Observe where the other ray intersects the protractor’s scale.
- Read the angle measure in degrees from the scale.
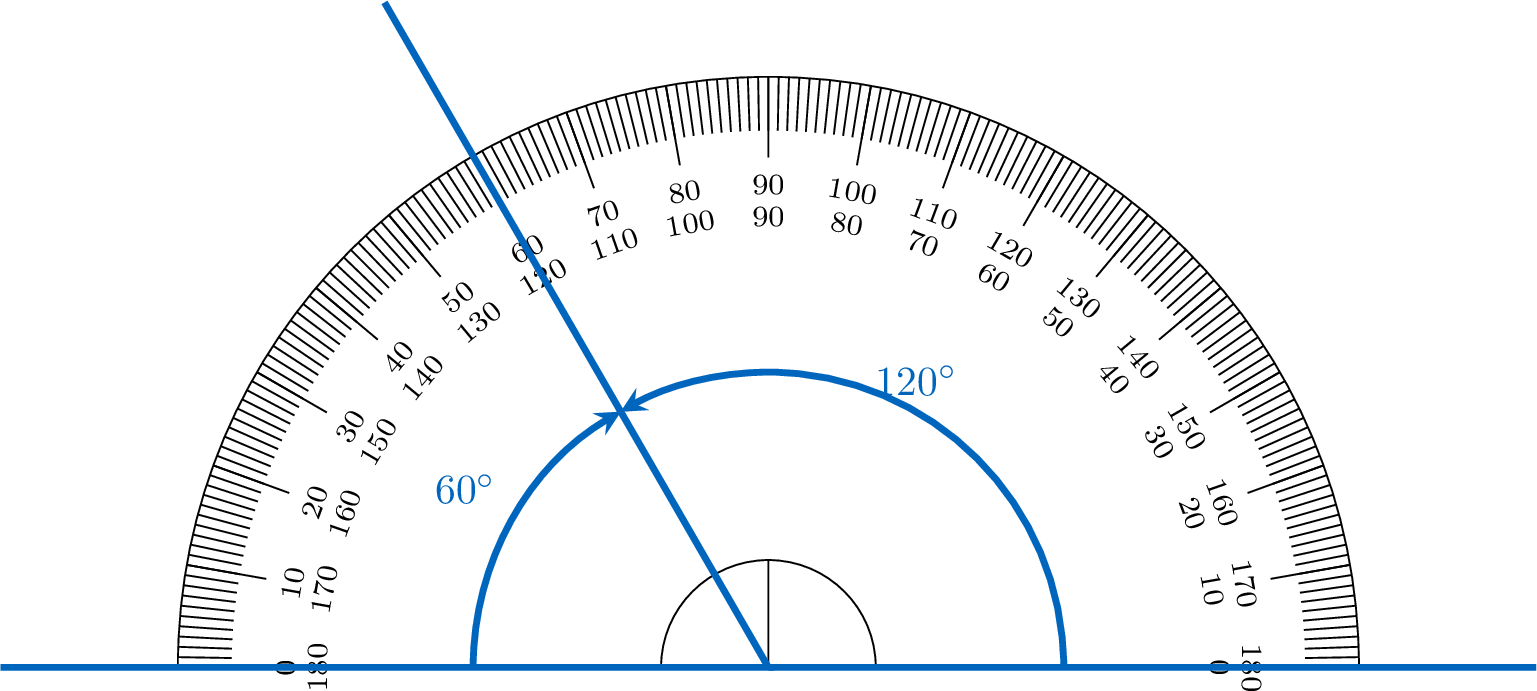
Example
Measure the following angle.

The angle measures \(140^\circ\).
Method Drawing an Angle with a Protractor
- Draw a ray starting from a point (the vertex).

- Place the protractor’s origin over the vertex and align the baseline with the ray.

- Locate the desired angle measure on the protractor’s scale and mark the point.
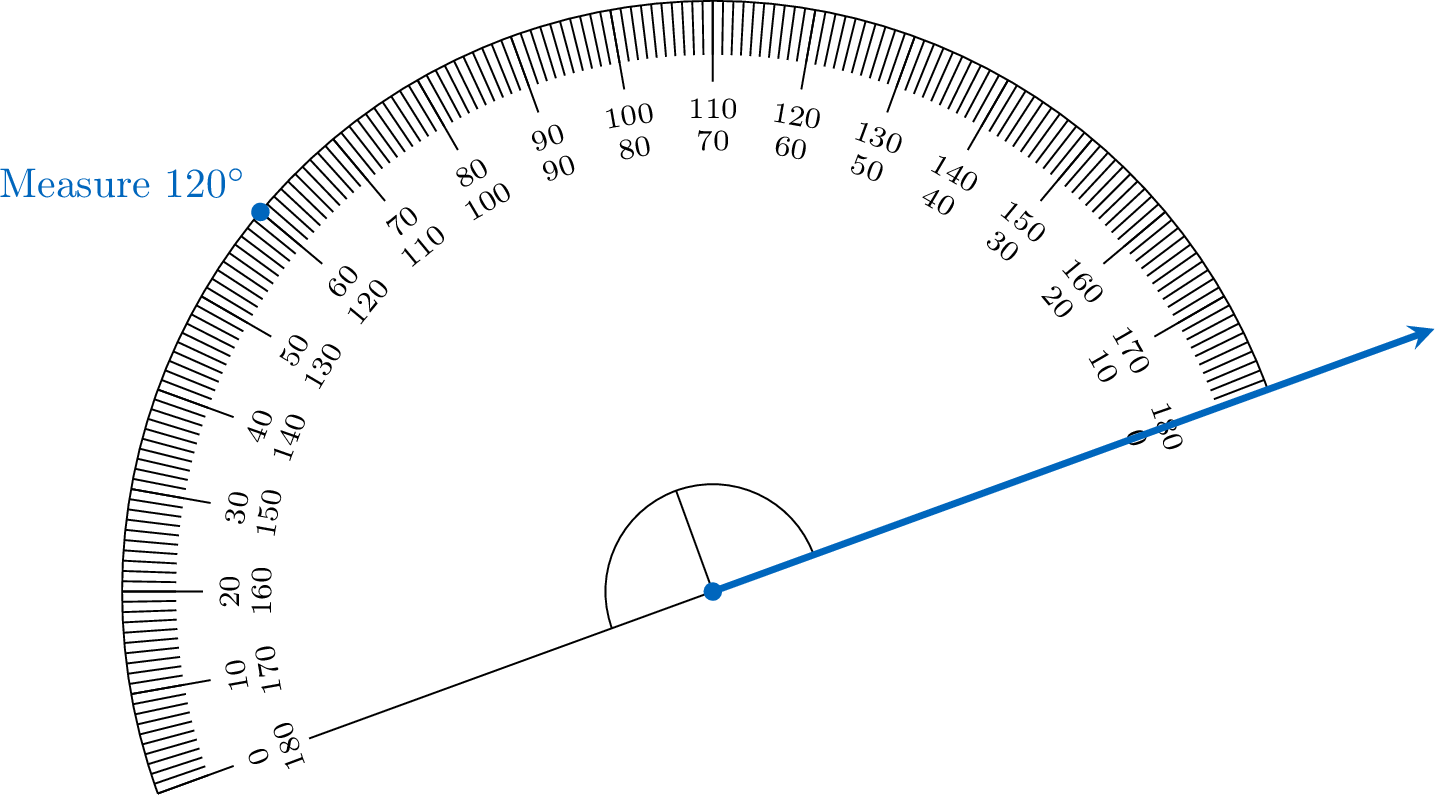
- Draw a second ray from the vertex through the marked point to form the angle.
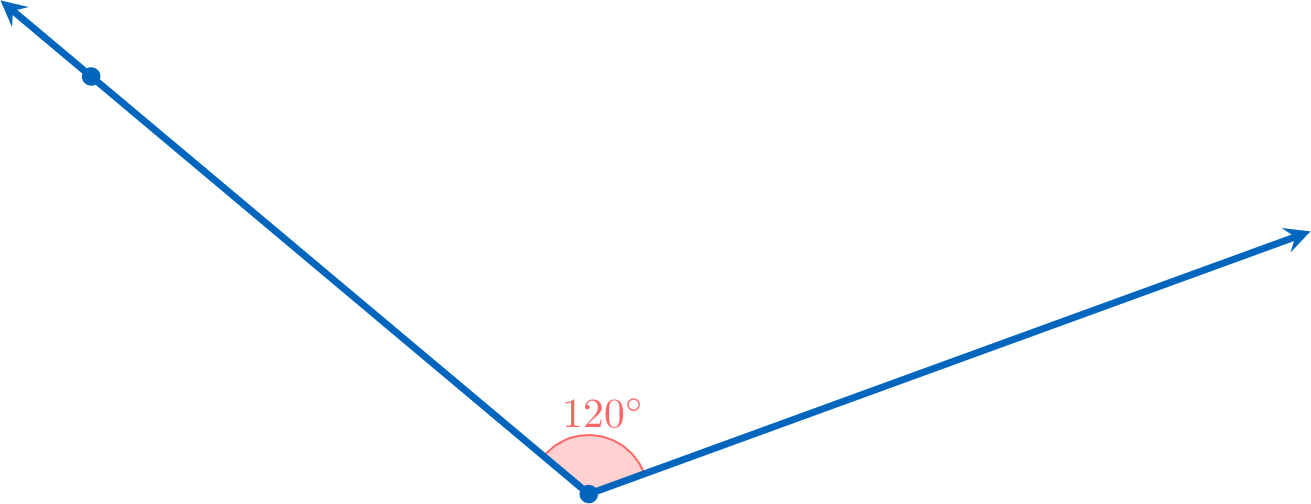
Classification of Angles
In geometry, angles are classified based on their measure. The following table defines four main types of angles: straight, right, acute, and obtuse.
Definition Classification of Angles
| Name | Fraction of a Circle | Angle Measure | Figure |
| Acute Angle | Less than \(\dfrac{1}{4}\) | Less than \(90^{\circ}\) | |
| Right Angle | \(\dfrac{1}{4}\) | \(\dfrac{1}{4} \text{ of } 360^{\circ} = 90^{\circ}\) | 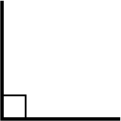 |
| Obtuse Angle | Between \(\dfrac{1}{4}\) and \(\dfrac{1}{2}\) | Between \(90^{\circ}\) and \(180^{\circ}\) | |
| Straight Angle | \(\dfrac{1}{2}\) | \(\dfrac{1}{2} \text{ of } 360^{\circ} = 180^{\circ}\) | |