Elements of Geometry
Point
Definition Point
A point is a single location in space, represented by a dot.
Definition Point Notation
A point is named using a capital letter, written as \(A\).
Points have no size, shape, or dimension. They simply mark a position.
Example
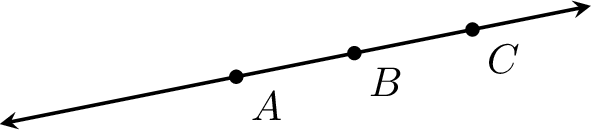
The diagram below shows three points labeled \(A\), \(B\), and \(C\):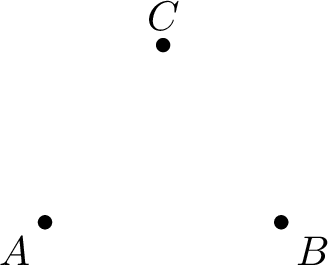
Lines, Segments and Rays
Definition Line
A line is a straight collection of points that extends infinitely in both directions.
Definition Line Notation
- A line can be named with a lowercase letter, written as \(\Line{l}\).
- A line is named using two points on it, written as \(\Line{AB}\).
Example
Name the line shown below: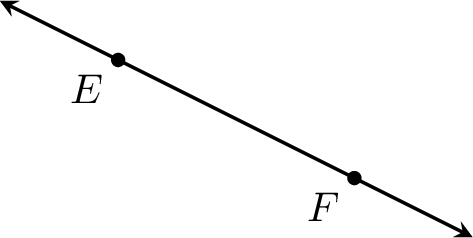
The line is \(\Line{EF}\).
Definition Line Segment
A line segment is a part of a line with two endpoints. It has a definite length.
Definition Line Segment Notation
A line segment is named by its endpoints, written as \(\Segment{AB}\).
Example
Name the segment shown below:
The segment is \(\Segment{EF}\).
Definition Ray
A ray is a part of a line that starts at one endpoint and extends infinitely in one direction.
Definition Ray Notation
A ray is named by its endpoint and another point on it, written as \(\Ray{AB}\).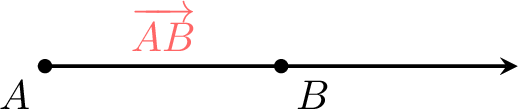
Example
Name the ray shown below:
The ray is \(\Ray{EF}\).
Definition Collinear Points
Collinear points are points that all lie on the same straight line.
Example
The points \(A\), \(B\) and \(C\) are collinear points.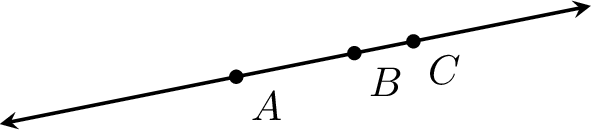
Element Relation
Definition Element Relation
The relation is a point of (or "is an element of") is used to show that a point lies on a geometric figure, such as a line or segment. It is denoted by the symbol \(\in\).
Example
\(C \in \Line{AB}\) and \(C \notin \Segment{AB}\)Length
Definition Length of a Line Segment
The length of a line segment is the distance between its two endpoints.
Definition Length Notation
The length of a line segment is denoted by its endpoints, written as \(AB\).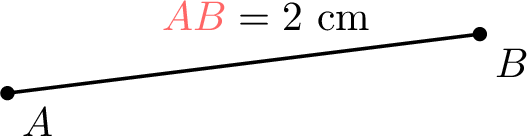
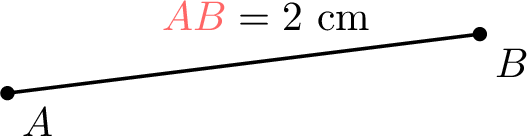
Definition Equal Lengths
Line segments are equal in length if they have the same length. We use tick marks to show they are equal.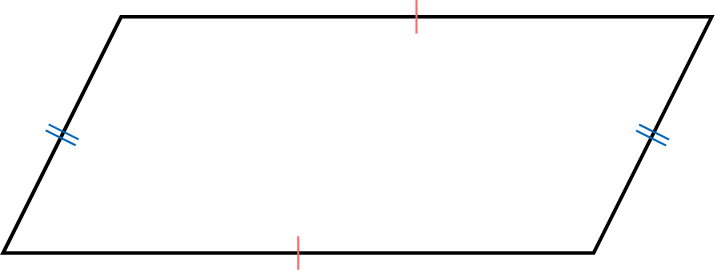
Example
Identify two segments that have the same length.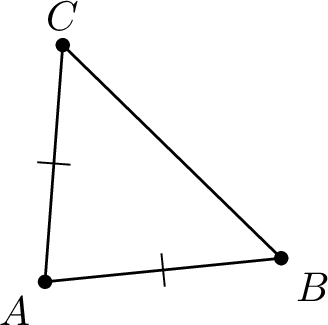
Segments \(\Segment{AB}\) and \(\Segment{AC}\) have the same length, as shown by their identical tick marks. Therefore, \(AB = AC\).
Method Measuring Length
We measure the length of a segment using a ruler by aligning one endpoint with the zero mark and reading the measurement at the other endpoint.
Example
Measure the length of segment \(\Segment{AB}\).
By aligning a ruler with segment \(\Segment{AB}\), the length is measured as \(AB = 4 \, \text{cm}\).
Intersection Point
Definition Intersection Point
An intersection point is a point where two or more geometric objects, such as lines or segments, meet.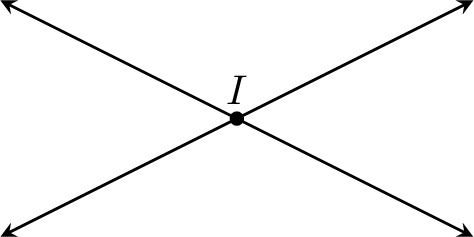
Example
Find the intersection point of the lines \(\Line{AB}\) and \(\Line{CD}\).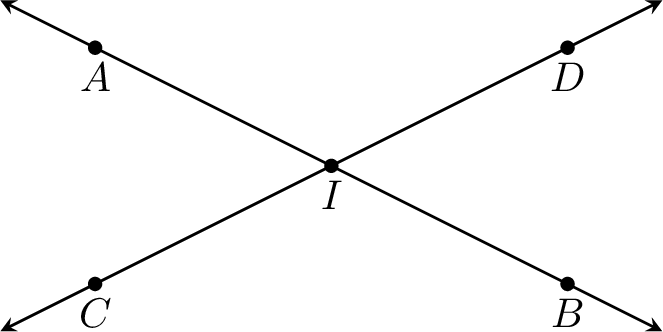
The intersection point is \(I\).
Parallel Lines
Definition Parallel Lines
Two parallel lines are lines that never intersect, no matter how far they extend.
Definition Parallel Line Notation
Parallel lines are indicated using matching arrowheads on each line.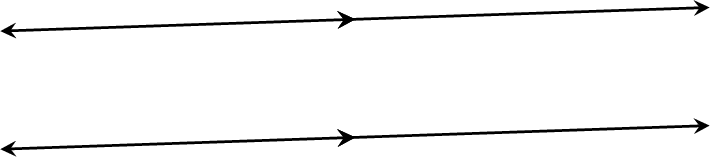
Perpendicular Lines
Definition Perpendicular Lines
Two perpendicular lines are lines that intersect at a right angle (90 degrees).
Example
Identify the perpendicular lines in the figure below: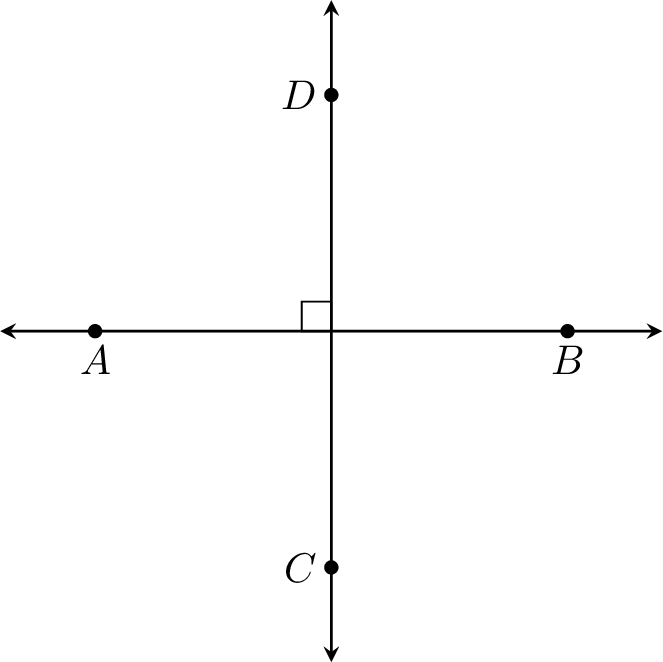
The lines \(\Line{AB}\) and \(\Line{CD}\) are perpendicular, as they intersect forming a right angle, indicated by the right-angle mark.
Midpoint and Perpendicular Bisector
Definition Midpoint of a Line Segment
The midpoint of a line segment is a point that lies on the segment and divides it into two segments of equal length.
Proposition Midpoint Length Property
If point \(I\) is the midpoint of segment \(\Segment{AB}\), then \(AB = 2 \times AI\) and \(AI = \frac{AB}{2}\).
$$\begin{aligned}AB &= AI + IB&( I \text{ is the midpoint of } \Segment{AB})\\&= AI + AI\\& = 2 \times AI\end{aligned}$$Thus, \(AB = 2 \times AI\). To find \(AI\) in terms of \(AB\), we rearrange the equation:$$AI = \frac{AB}{2}.$$
Definition Perpendicular bisector
The perpendicular bisector of a line segment is a line which meets the segment at its midpoint perpendicularly.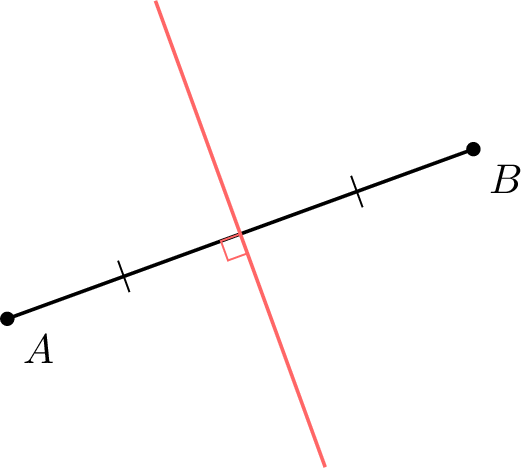
Method Constructing the Perpendicular Bisector of \(\Segment{AB}\)
- Construct two arcs of circles with the same radius and centers at \(A\) and \(B\).
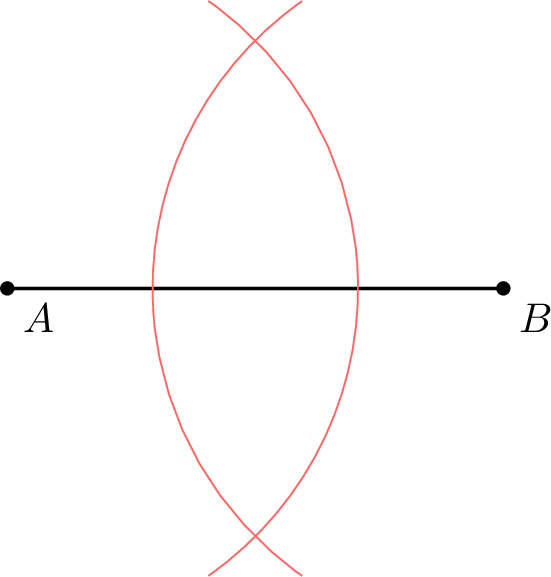
- The arcs intersect at points \(E\) and \(F\).
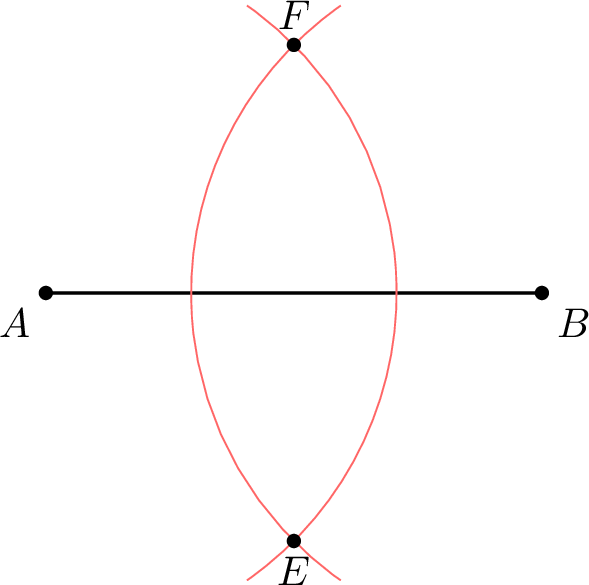
- The perpendicular bisector of \(\Segment{AB}\) is the line \(\Line{EF}\).
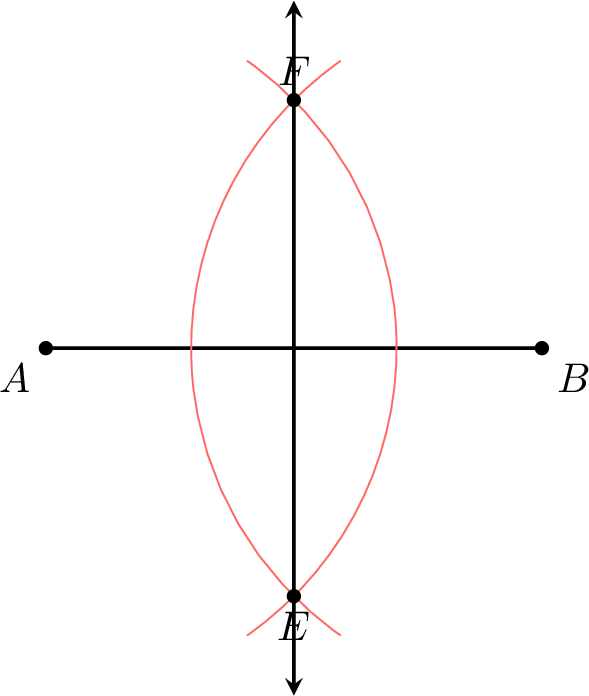
Properties of Parallel Lines
Proposition Properties of Parallel Lines
- If line \(\Line{l_1}\) is parallel to line \(\Line{l_2}\), and line \(\Line{l_2}\) is parallel to line \(\Line{l_3}\), then line \(\Line{l_1}\) is parallel to line \(\Line{l_3}\).
If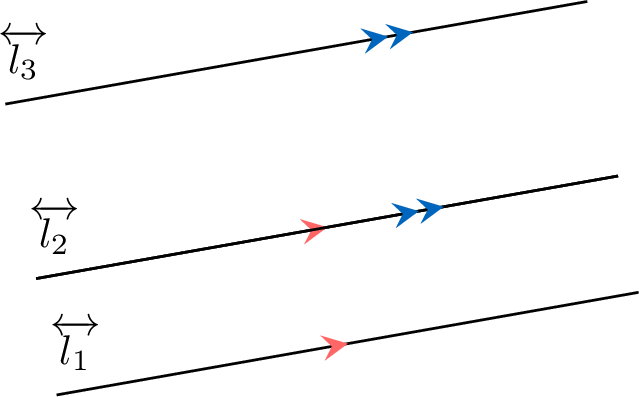 
, then 
. - If line \(\Line{l_1}\) is perpendicular to line \(\Line{l_3}\), and line \(\Line{l_2}\) is perpendicular to line \(\Line{l_3}\), then line \(\Line{l_1}\) is parallel to line \(\Line{l_2}\).
If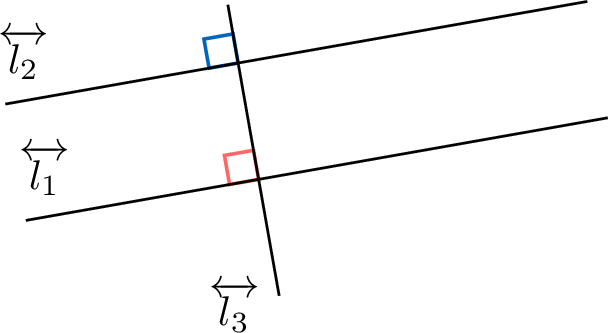 
, then 
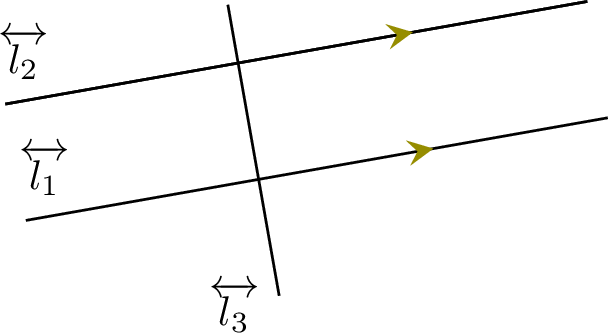. - If line \(\Line{l_1}\) is parallel to line \(\Line{l_2}\), and line \(\Line{l_1}\) is perpendicular to line \(\Line{l_3}\), then line \(\Line{l_2}\) is perpendicular to line \(\Line{l_3}\).
If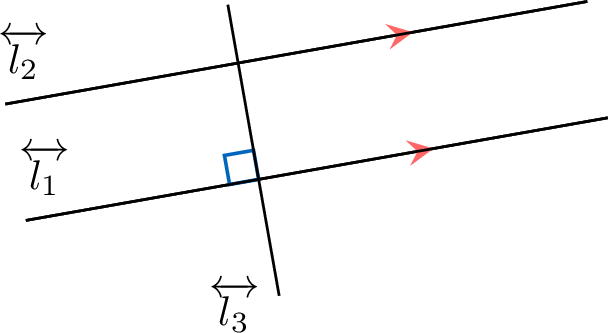 
, then 
.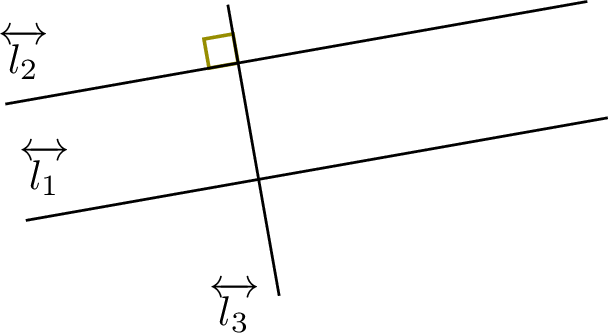