Volume
What is Volume?
Definition Volume
The volume of an object is the amount of space it takes up. We measure volume by counting how many cubic units can fit inside it. A cubic unit is a cube with sides that are 1 unit long.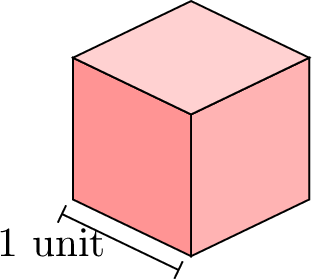

Method Counting Cubes to Find Volume
To find the volume of a shape made of blocks, simply count the total number of blocks (cubic units) it is made from. A good strategy is to count the blocks in each layer.
Example
Find the volume of the shape below.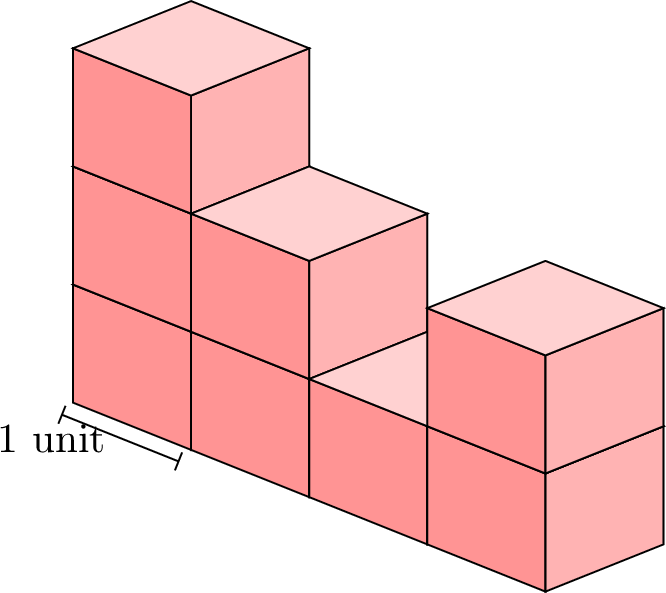

We can find the volume by counting the cubes in the shape. Each small cube has a volume of 1 cubic unit.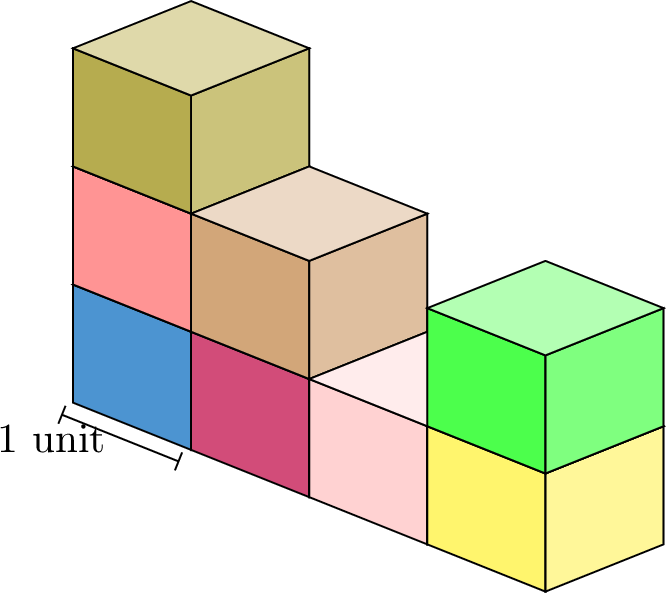

Units of Volume
When we measure volume, it is important to use standard units so that everyone gets the same measurement. Non-standard units, like different-sized building blocks, can give different answers.
For volume, we use standard units like the cubic centimeter, written \(\text{cm}^3\), and the cubic meter, written \(\text{m}^3\).
For volume, we use standard units like the cubic centimeter, written \(\text{cm}^3\), and the cubic meter, written \(\text{m}^3\).
Definition Units of Volume
- Cubic centimeter \(\left(\mathrm{cm}^3\right)\):The volume of a cube with sides \(1\ \text{cm}\) long. This is about the volume of a small ice cube.
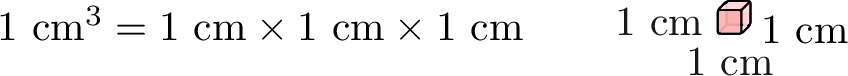 \(\quad\)
\(\quad\)
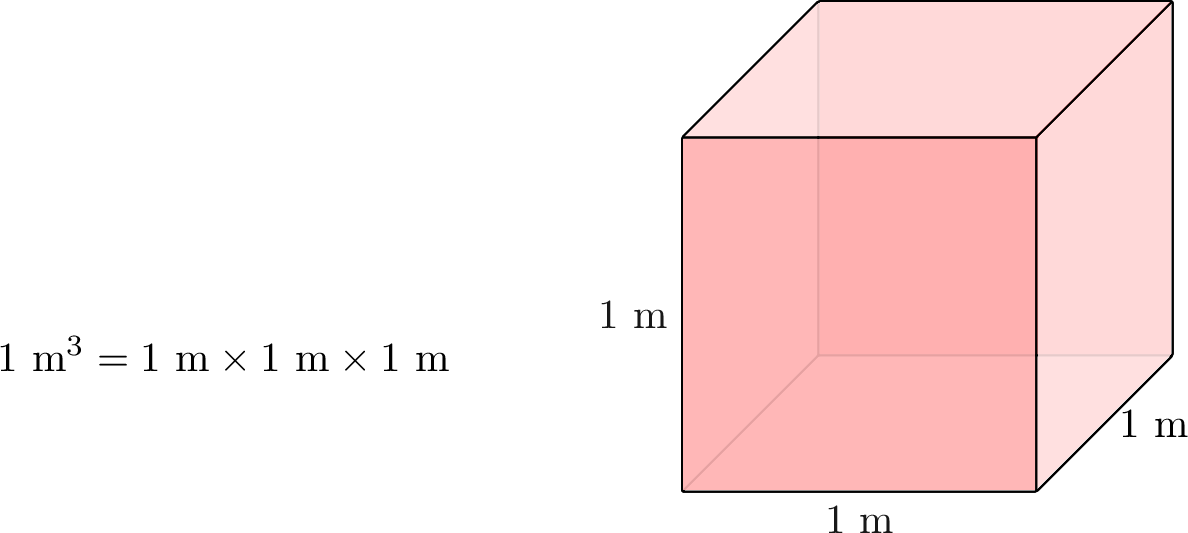
- Cubic meter \(\left(\mathrm{m}^3\right)\):The volume of a cube with sides \(1\ \text{m}\) long. This is about the volume of a washing machine.
 \(\quad\)
\(\quad\)
Volume of a Rectangular Cuboid
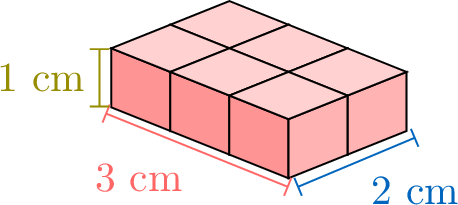
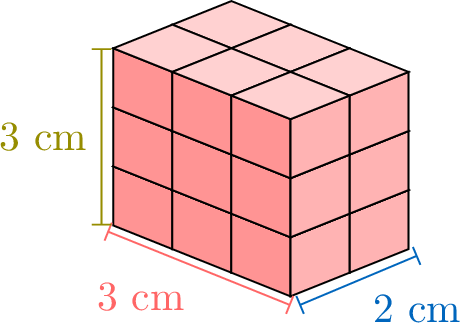
Counting every little cube inside a rectangular box (rectangular cuboid) gives its volume, but that is slow. Instead, imagine making the box taller one layer at a time and watching how the volume grows.
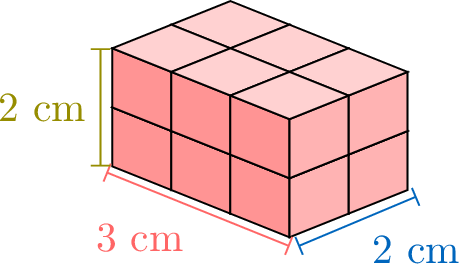
Each new layer adds the same number of cubes. By counting layer by layer, we spot a pattern and get a quick rule for volume: we can multiply the \(\textcolor{colordef}{length}\), the \(\textcolor{colorprop}{width}\), and the \(\textcolor{olive}{height}\).
Each new layer adds the same number of cubes. By counting layer by layer, we spot a pattern and get a quick rule for volume: we can multiply the \(\textcolor{colordef}{length}\), the \(\textcolor{colorprop}{width}\), and the \(\textcolor{olive}{height}\).
 \(\quad\quad\)
\(\quad\quad\)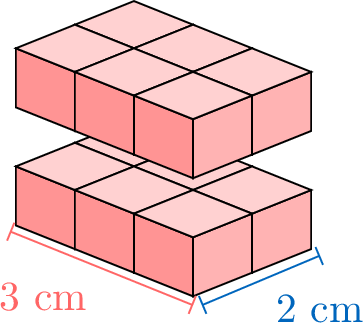
 \(\quad\quad\)
\(\quad\quad\)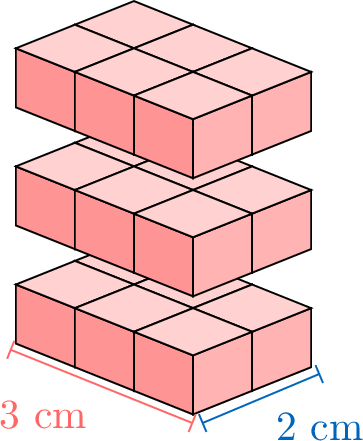
 \(\quad\quad\)
\(\quad\quad\)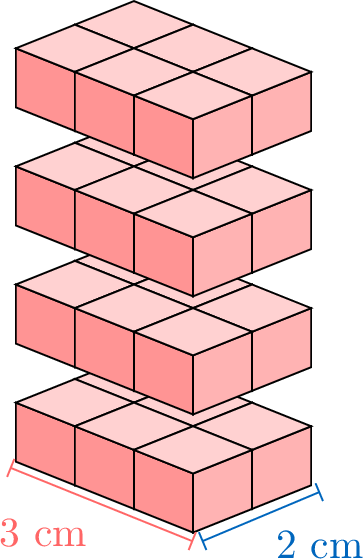
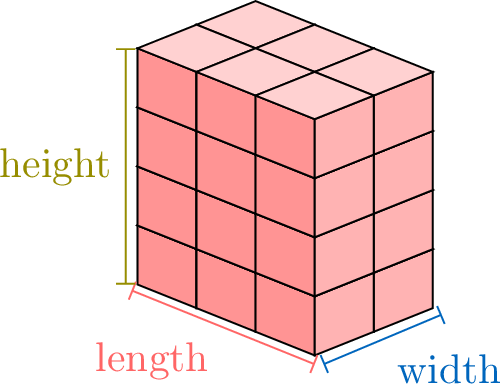
Proposition Volume of a Rectangular Cuboid
The volume of a rectangular cuboid (also called a rectangular prism) is found by multiplying its length, width, and height:$$\text{Volume} = \textcolor{colordef}{\text{length}} \times \textcolor{colorprop}{\text{width}} \times \textcolor{olive}{\text{height}}$$$$V = \textcolor{colordef}{l} \times \textcolor{colorprop}{w} \times \textcolor{olive}{h}$$

Example
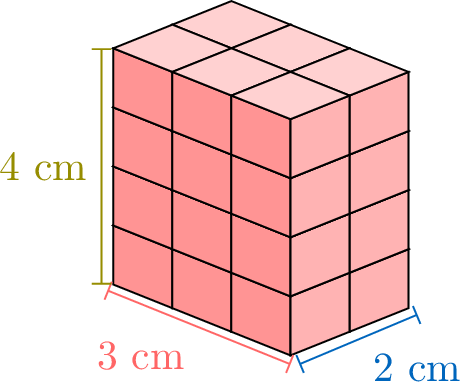
Find the volume of this rectangular cuboid.

Using the formula for the volume of a rectangular cuboid:$$\begin{aligned}\text{Volume} &= \textcolor{colordef}{\text{length}} \times \textcolor{colorprop}{\text{width}} \times \textcolor{olive}{\text{height}}\\
&= 3\times 2 \times 4 \\
&= 24 \, \text{cm}^3\end{aligned}$$