Probability
Ever wondered if it'll rain tomorrow or if you'll win a game? That's probability! It's a mathematical way to measure how likely events are to happen.
Algebra of Events
Sample Spaces
Definition Outcome
An outcome is one possible result of a random experiment.
Example
What are the outcomes when you flip a coin? 
The outcomes are Heads (H)= and Tails (T)=
and Tails (T)= .
.
Example
What are the outcomes when you roll a six-sided die?
The outcomes are 1= ,2=
,2=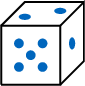 ,3=
,3=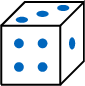 ,4=
,4= ,5=
,5=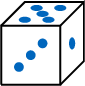 ,and 6=
,and 6=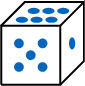 .
.
Definition Sample Space
The sample space is the set of all possible outcomes of a random experiment.
Example
What’s the sample space when you flip a coin?
The sample space is \(\{\)Heads, Tails\(\}=\{\) ,
, \(\}\), or just \(\{\)H, T\(\}\) for short.
\(\}\), or just \(\{\)H, T\(\}\) for short.
Example
What’s the sample space when you roll a six-sided die?
The sample space is \(\{\)1, 2, 3, 4, 5, 6\(\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\).
\(\}\).
Events
Definition Event
Un événement est un sous-ensemble des issues possibles de l’univers. We write it \(E\).
Example
In the experiment of rolling a die, find \(E\) the event of rolling an even number.
Among the outcomes of the sample space \(\{\)1, 2, 3, 4, 5, 6\(\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\) ,the event of rolling an even number is \(E = \{2, 4, 6\}=\{\)
\(\}\) ,the event of rolling an even number is \(E = \{2, 4, 6\}=\{\) ,
, ,
, \(\}\).
\(\}\).
Complementary Events
Ever wonder what happens if you look for everything except a certain event? That’s where the complementary event comes in! It’s just everything in the sample space that isn’t in your event. We usually write it as \(E'\) (“\(E\)-prime”).
Definition Complementary Event
The complementary event of an event \(E\) is all the outcomes in the sample space that are not in \(E\). We write it \(E'\).
Example
In the experiment of rolling a die, let \(E\) the event of rolling an even number. Find \(E'\).
The sample space is \(\{1, 2, 3, 4, 5, 6\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\) and \(E = \{2, 4, 6\}=\{\)
\(\}\) and \(E = \{2, 4, 6\}=\{\) ,
, ,
, \(\}\).
\(\}\).
So \(E'\) is all the other numbers: \(\{1, 3, 5\}=\{\) ,
, ,
, \(\}\). These are the odd numbers.
\(\}\). These are the odd numbers.
So \(E'\) is all the other numbers: \(\{1, 3, 5\}=\{\)
Multi-Step Random Experiments
A multi-step random experiment is an experiment that involves a sequence of actions, where each action (or step) has its own set of possible outcomes. For example, tossing two coins is a multi-step experiment because it consists of two separate coin tosses:
Using different representations—such as grids, tables, tree diagrams, or simply listing the outcomes—helps us organize and visualize all the possible combinations that result from multiple steps.
- The first coin toss (step 1) can result in Heads (H) or Tails (T).
- The second coin toss (step 2) can also result in Heads (H) or Tails (T).
Using different representations—such as grids, tables, tree diagrams, or simply listing the outcomes—helps us organize and visualize all the possible combinations that result from multiple steps.
Method Representations of Multi-Step Random Experiments
When an experiment involves more than one step, we can represent the sample space (the set of all possible outcomes) in several ways:
- using a grid (to visually map combinations along two axes),
- using a table (to organize outcomes in rows and columns),
- using a tree diagram (to show each sequential step), or
- by listing all possible outcomes.
Example
For the random experiment of tossing two coins, display the sample space by:
- using a grid
- using a table
- using a tree diagram
- listing all possible outcomes
- Grid:
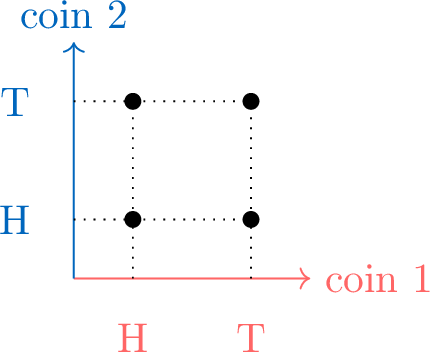
- Table:
\(\begin{aligned} & \textcolor{colorprop}{\text{coin 2}} \\ \textcolor{colordef}{\text{coin 1}} \end{aligned} \) \(\textcolor{colorprop}{H}\) \(\textcolor{colorprop}{T}\) \(\textcolor{colordef}{H}\) \(\textcolor{colordef}{H}\textcolor{colorprop}{H}\) \(\textcolor{colordef}{H}\textcolor{colorprop}{T}\) \(\textcolor{colordef}{T}\) \(\textcolor{colordef}{T}\textcolor{colorprop}{H}\) \(\textcolor{colordef}{T}\textcolor{colorprop}{T}\) - Tree diagram:
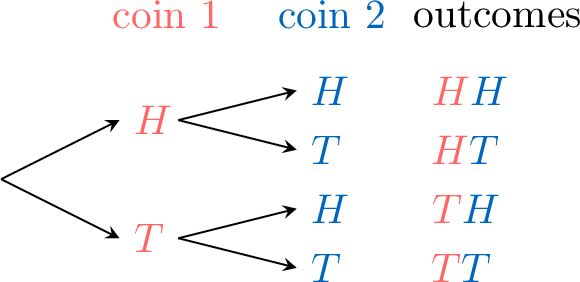
- List:\(\{\textcolor{colordef}{H}\textcolor{colorprop}{H}, \textcolor{colordef}{H}\textcolor{colorprop}{T},\textcolor{colordef}{T}\textcolor{colorprop}{H}, \textcolor{colordef}{T}\textcolor{colorprop}{T}\}\)
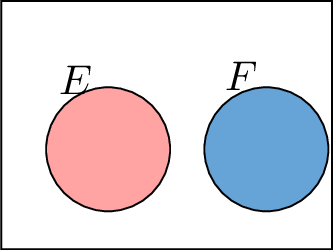
\(E\) or \(F\)
Definition \(E\) or \(F\)
The union of two events \(E\) and \(F\), denoted as \(E \text{ or } F\) or \(E \cup F\), is the event that occurs if at least one of the events \(E\) or \(F\) happens (i.e., if \(E\) occurs, or \(F\) occurs, or both occur).
Example
Consider the roll of a standard six-sided die.
Let event \(E\) be the event of rolling an even number: \(E = \{2, 4, 6\}\).
Let event \(F\) be the event of rolling a number less than 4: \(F = \{1, 2, 3\}\).
Find the event \(E\) or \(F\).
Let event \(E\) be the event of rolling an even number: \(E = \{2, 4, 6\}\).
Let event \(F\) be the event of rolling a number less than 4: \(F = \{1, 2, 3\}\).
Find the event \(E\) or \(F\).
\(E\) or \(F\) includes all outcomes from both event sets.
So, \(E \text{ or } F = E \cup F = \{1, 2, 3, 4, 6\}\).
So, \(E \text{ or } F = E \cup F = \{1, 2, 3, 4, 6\}\).
\(E\) and \(F\)
Definition \(E\) and \(F\)
The intersection of two events \(E\) and \(F\), denoted as \(E \text{ and } F\) or \(E \cap F\), is the set of all outcomes that are common to both \(E\) and \(F\). The event \(E\) and \(F\) occurs if and only if both \(E\) and \(F\) happen simultaneously.
Example
Consider the roll of a standard six-sided die.
Let event \(E\) be the event of rolling an odd number: \(E = \{1, 3, 5\}\).
Let event \(F\) be the event of rolling a number less than 4: \(F = \{1, 2, 3\}\).
Find the event \(E\) and \(F\).
Let event \(E\) be the event of rolling an odd number: \(E = \{1, 3, 5\}\).
Let event \(F\) be the event of rolling a number less than 4: \(F = \{1, 2, 3\}\).
Find the event \(E\) and \(F\).
\(E\) and \(F\) includes all outcomes that are common to both \(E\) and \(F\).
So, \(E \text{ and } F = E \cap F = \{1, 3\}\).
So, \(E \text{ and } F = E \cap F = \{1, 3\}\).
Mutually Exclusive
Definition Mutually Exclusive
Two events \(E\) and \(F\) are said to be mutually exclusive if they cannot occur at the same time. In other words, the occurrence of event \(E\) excludes the possibility of event \(F\) occurring, and vice versa. This is mathematically represented as:$$E \text{ and } F = E \cap F = \emptyset,$$where \(\emptyset\) denotes the empty set, indicating that there are no outcomes common to both \(E\) and \(F\).
Example
Consider the roll of a standard six-sided die.
Let event \(E\) be the event of rolling an odd number: \(E = \{1, 3, 5\}\).
Let event \(F\) be the event of rolling an even number: \(F = \{2, 4, 6\}\).
Show that \(E\) and \(F\) are mutually exclusive.
Let event \(E\) be the event of rolling an odd number: \(E = \{1, 3, 5\}\).
Let event \(F\) be the event of rolling an even number: \(F = \{2, 4, 6\}\).
Show that \(E\) and \(F\) are mutually exclusive.
There are no outcomes common to both \(E\) and \(F\):$$E \cap F = \emptyset.$$Thus, the events \(E\) and \(F\) are mutually exclusive.
Venn Diagram
Definition Correspondence Between Set Theory and Probabilistic Vocabulary
| Notation | Set Vocabulary | Probabilistic Vocabulary | Venn Diagram |
| \(U\) | Universal set | Sample space |  |
| \(x\) | Element of \(U\) | Outcome |  |
| \(\emptyset\) | Empty set | Impossible event | |
| \(E\) | Subset of \(U\) | Event | 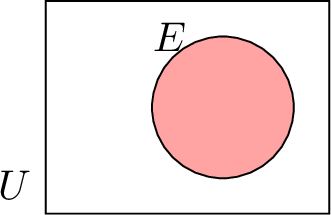 |
| \(x \in E\) | \(x\) is an element of \(E\) | \(x\) is an outcome of \(E\) |  |
| \(E'\) | Complement of \(E\) in \(U\) | Complement of \(E\) in \(U\) | 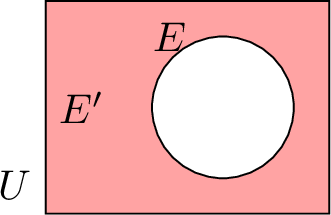 |
| \(E \text{ or } F\) | Union of \(E\) and \(F\): \(E \cup F\) | \(E\) or \(F\) | 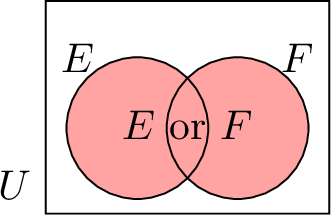 |
| \(E \text{ and } F\) | Intersection of \(E\) and \(F\): \(E \cap F\) | \(E\) and \(F\) | 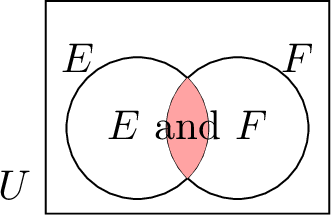 |
| \(E \cap F = \emptyset\) | \(E\) and \(F\) are disjoint | \(E\) and \(F\) are mutually exclusive | 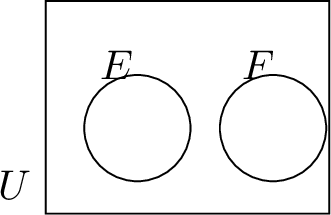 |
Probability
Probability Axioms
When you flip a coin, there are two possible outcomes: heads or tails. The chance of getting heads is the same as getting tails—it’s 1 out of 2! In math, we write:

Definition Probability
The probability of an event \(E\), written \(P(E)\), is a number that tells us how likely the event is to happen. It's always between 0 (impossible) and 1 (certain).

Example
The probability of an event "even chance" can be represented as:
- Fraction: \( \frac{1}{2} \)
- Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: \( 1 \div 2 = 0.5 \).
- Percentage: To convert the decimal to a percentage, multiply by \(100\pourcent\): \( 0.5 \times 100\pourcent = 50\pourcent \).
Definition Probability Axioms
\(P\) is a probability if:
- \(0 \leqslant P(E) \leqslant 1\), for any event \(E\),
- \(P(U) = 1\),
- If \(E\) and \(F\) are mutually exclusive events, then \(P(E \text{ or } F) = P(E) + P(F)\).
- The probability of an event \(E\), \(\textcolor{colordef}{P(E)}\), is represented by the shaded area of the event in a Venn diagram:

- The first axiom states that the probability of an event \(E\) is a value between 0 and 1, inclusive.
- The second axiom states that the probability of the sample space \(U\) is equal to \(1\), i.e., \(100\pourcent\). This is because the sample space \(U\) includes all possible outcomes of a random experiment, so the event \(U\) always occurs, and \(P(U) = 1\). In a Venn diagram, this is represented as the entire shaded area of the sample space:
 $$\textcolor{colordef}{P(U)} = 1$$
$$\textcolor{colordef}{P(U)} = 1$$ - The third axiom states that if two events are mutually exclusive (i.e., they cannot occur simultaneously), then the probability of their union is the sum of their individual probabilities. In a Venn diagram, for two mutually exclusive events (with no overlap), the total area of their union is the sum of the individual areas:
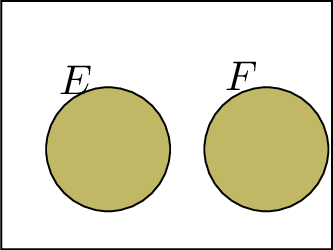 =
=
Probability Rules
Ever wondered how to quickly find the chance that something doesn’t happen? There’s a shortcut for that! It’s called the complement rule.
Proposition Complement Rule
For any event \(E\) with complementary event \(E'\),$$\textcolor{colordef}{P(E)} + \textcolor{colorprop}{P(E')} = 1$$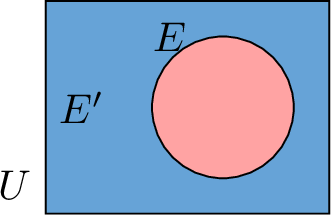

The green area, \(\textcolor{olive}{P(U)}\), ,is the sum of the red area, \(P(E)\), and the blue area, \(P(E')\),
,is the sum of the red area, \(P(E)\), and the blue area, \(P(E')\),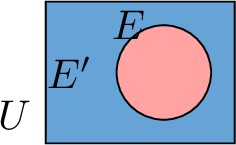 .
.
So,$$\textcolor{colordef}{P(E)} + \textcolor{colorprop}{P(E')} = \textcolor{olive}{P(U)}$$Since \(\textcolor{olive}{P(U) = 1}\), we have:$$\textcolor{colordef}{P(E)} + \textcolor{colorprop}{P(E')} = 1$$
 ,is the sum of the red area, \(P(E)\), and the blue area, \(P(E')\),
,is the sum of the red area, \(P(E)\), and the blue area, \(P(E')\), .
.So,$$\textcolor{colordef}{P(E)} + \textcolor{colorprop}{P(E')} = \textcolor{olive}{P(U)}$$Since \(\textcolor{olive}{P(U) = 1}\), we have:$$\textcolor{colordef}{P(E)} + \textcolor{colorprop}{P(E')} = 1$$
Example
Farid has a \(0.8\) (80\(\pourcent\)) chance of finishing his homework on time tonight (event \(E\)). What’s the chance he doesn’t finish on time?
The complementary event \(E'\) is “Farid does not finish his homework on time.” By the complement rule:$$\begin{aligned}P(E') &= 1 - P(E) \\
&= 1 - 0.8 \\
&= 0.2\end{aligned}$$So, there’s a \(0.2\) (or 20\(\pourcent\)) chance he doesn’t finish on time!
Proposition Addition Law of Probability
For any events \(E\) and \(F\),$$P(E \text{ or } F) = P(E) + P(F) - P(E \text{ and } F)$$
Example
A local high school is holding a talent show where students can participate in singing, dancing, or both. The probability that a randomly selected student participates in singing is \(0.4\), the probability that a student participates in dancing is \(0.3\), and the probability that a student participates in both singing and dancing is \(0.1\). Find the probability that a randomly selected student participates in either singing or dancing.
- Let \(S\) be the event "participates in singing", and \(D\) the event "participates in dancing". We are given \(P(S) = 0.4\), \(P(D) = 0.3\), and \(P(S \text{ and } D) = 0.1\).
- The probability that a student participates in either singing or dancing is \(P(S \text{ or } D)\).
- By the addition law of probability:$$\begin{aligned}P(S \text{ or } D) &= P(S) + P(D) - P(S \text{ and } D) \\ &= 0.4 + 0.3 - 0.1 \\ &= 0.6\end{aligned}$$
- Therefore, the probability is \(\boxed{0.6}\).
Equally Likely
Have you ever flipped a fair coin or rolled a fair die? In these experiments, each outcome is just as likely as the others. We call these equally likely outcomes.
Definition Equally Likely
When all outcomes are equally likely, the probability of an event \(E\) is:$$\begin{aligned}P(E) &= \frac{\text{number of outcomes in the event}}{\text{number of outcomes in the sample space}}\\
&=\dfrac{\Card{E}}{\Card{U}}\\
\end{aligned}$$
Example
What’s the probability of rolling an even number with a fair six-sided die?
- Sample space = \(\{1, 2, 3, 4, 5, 6\}\) (6 outcomes).
- \(E = \{2, 4, 6\}\) (3 outcomes).
- $$\begin{aligned}P(E) &= \frac{3}{6} \\ &= \frac{1}{2}\end{aligned}$$
Probability of Independent Events
Independent events are situations where what happens in one event does not affect what happens in the other. For example: rolling two dice at the same time. The result of the first die doesn’t change the chances for the second die—they are independent!
Definition Independent Events
Two events, \(A\) and \(B\), are independent if the chance of both happening is just the product of their individual chances. Mathematically:$$P(A \text{ and } B) = P(A) \times P(B)$$
Example
Imagine you do two totally separate actions:
- Flipping a fair coin (heads or tails).
- Rolling a fair six-sided die (1, 2, 3, 4, 5, or 6).
Let’s break it down:
- These events are independent, so we multiply their probabilities.
- For the coin: You’ve got two options—heads or tails—and they’re equally likely. So, \(P(\text{"tails"}) = \dfrac{1}{2}\).
- For the die: There are six sides, and “greater than 4” means 5 or 6. That’s 2 out of 6 possibilities, so \(P(\text{"number} > 4") = \dfrac{2}{6}=\dfrac{1}{3}\).
- Now, combine them:$$\begin{aligned}P(\text{"tails" and "number} > 4") &= P(\text{"tails"}) \times P(\text{"number} > 4") \\ &= \dfrac{1}{2} \times \dfrac{1}{3} \\ &= \dfrac{1}{6}\end{aligned}$$
- Result: There’s a \(\dfrac{1}{6}\) chance of landing tails and rolling a 5 or 6.
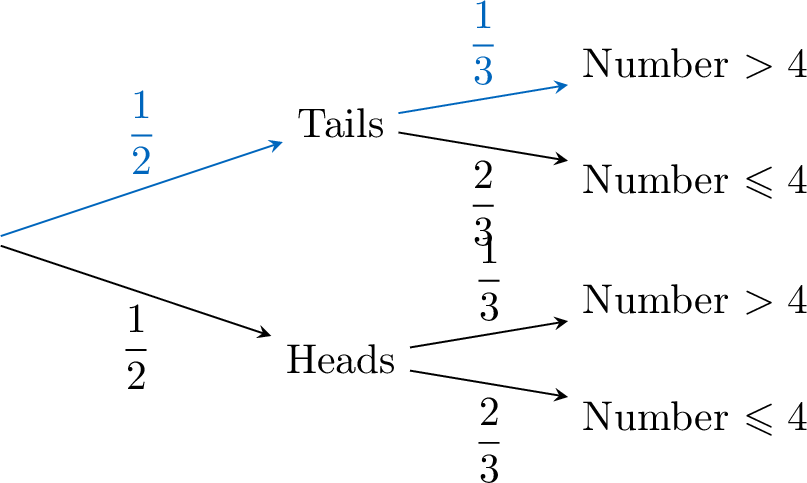
Method Finding the Probability of Two Independent Events using a Probability Tree Diagram
- Draw the tree: Start with two branches for the coin: “Heads” and “Tails.” From each, draw two branches for the die: “Number \(> 4\)” (5 or 6) and “Number \(\leqslant 4\)” (1, 2, 3, 4).
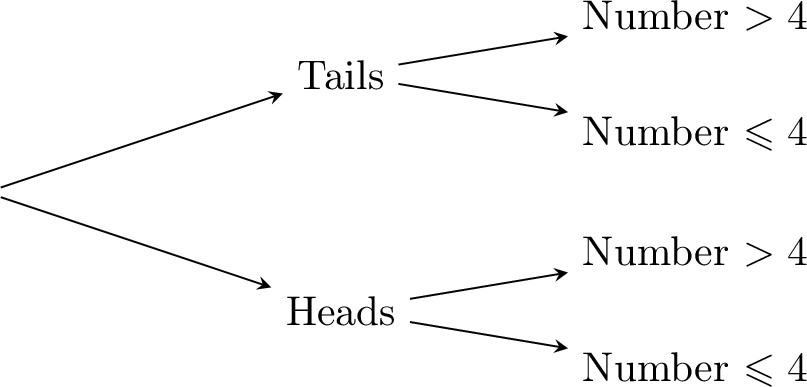
- Label probabilities: Each coin branch is \(\dfrac{1}{2}\). For the die, “Number \(> 4\)” is \(\dfrac{1}{3}\) (2 out of 6), “Number \(\leqslant 4\)” is \(\dfrac{4}{6} = \dfrac{2}{3}\).
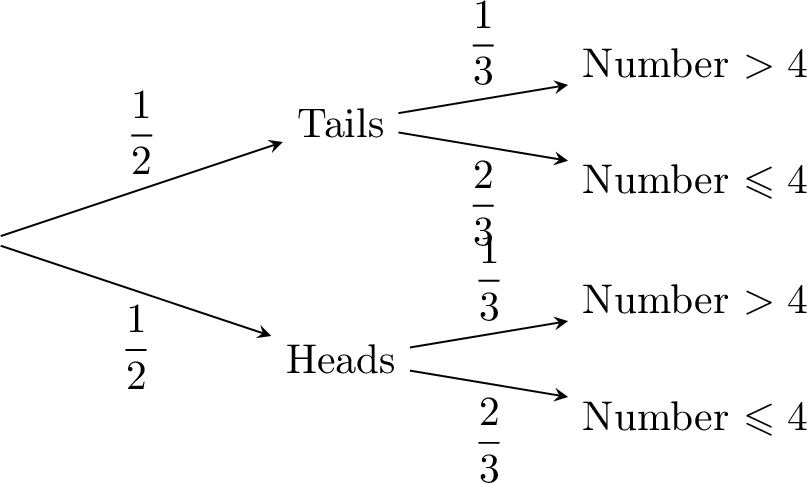
- Multiply the probabilities along the path: For “Tails” and “Number \(>4\)”:$$\dfrac{1}{2} \times \dfrac{1}{3} = \dfrac{1}{6}$$

Experimental Probability
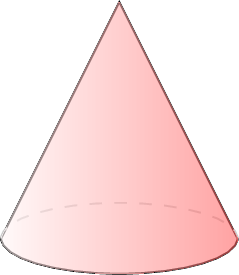
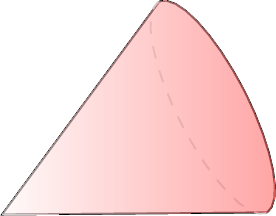
Isaac wishes to determine how a cone lands when tossed—base down or point down? The possible outcomes are as follows:
- Base down:
- Point down:
- Base down: 30 times.
- Point down: 20 times.
- \( P(\text{"base down"}) = \frac{30}{50} = 0.6 \) (60\(\pourcent\)).
- \( P(\text{"point down"}) = \frac{20}{50} = 0.4 \) (40\(\pourcent\)).
Theorem Law of Large Numbers
The probability of an event \(E\) can be estimated using the formula:$$P(E) \approx \frac{\text{number of times the event occurs}}{\text{number of trials}}$$Here, "trials" refer to the number of times the experiment is repeated.
Remark
More trials yield better estimates.