Set Theory

Definitions

Sets

Definition Set

A set is a collection of objects, called elements.
We list its elements between curly brackets.

Example

List all possible results when rolling a standard die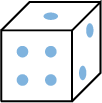

Answer

$E=\{1,2,3,4,5,6\}=\{$

$\}$.

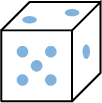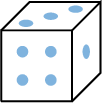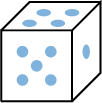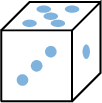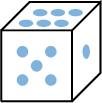Definition Element

An element is an object contained in a set.
$\in$ means "is an element of" or "belongs to".
$\notin$ means "is not an element of" or "does not belong to".

Example

$2\in \{1,2,3,4,5,6\}$ and $7\notin \{1,2,3,4,5,6\}$.

Definition Equal sets

Two sets are equal if they have exactly the same elements.

Example

Determine if the sets $\{2,6,4\}$ and $\{2,4,6\}$ are equal.

Answer

Yes, the sets $\{2,6,4\}$ and $\{2,4,6\}$ are equal because they contain the same elements: $2$, $4$, and $6$.

Example

Determine if the sets $\{1,2,3\}$ and $\{1,2,4\}$ are equal.

Answer

No, the sets $\{1,2,3\}$ and $\{1,2,4\}$ are not equal because element $3$ belongs to $\{1,2,3\}$ but not to $\{1,2,4\}$.

Definition Empty Set

The empty set is a set with no elements. It is written as $\{\}$ or $\emptyset$.

Natural Numbers

Definition Natural Numbers

The set of natural numbers, denoted $\N$, is the set of counting numbers starting from zero:$$\N = \{0, 1, 2, 3, 4, 5, 6, \dots\}$$

Subsets

Definition Subset

A set $A$ is a subset of a set $B$ if every element in $A$ is also in $B$. We write this as $A \subseteq B$.

Example

Is $A \subseteq B$ when $A = \{2, 4, 6\}$ and $B = \{1, 2, 3, 4, 5, 6\}$?

Answer

Check each element: $2$, $4$, and $6$ from $A$ are all in $B = \{1, 2, 3, 4, 5, 6\}$. Since every element of $A$ is in $B$, $A \subseteq B$.

Set-Builder Notation

Definition Set-Builder Notation

The set-builder notation is a way to describe a set by giving a rule that its elements must follow. It is written like this:$$\{x \in E \mid \text{condition on } x\}$$In this notation, $x$ represents an element from a set $E$, and the symbol $\mid$ (or sometimes $:$) separates $x$ from the condition it must meet.It reads: “the set of all $x$ in $E$ such that $x$ follows the given condition.”

Example

Let $E$ be the set of results from rolling a standard six-sided die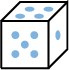

.
What are the elements of the set $\{x \in E \mid x \text{ is even}\}$?

Answer

The set $\{x \in E \mid x \text{ is even}\}$ contains all the even numbers in $E$. Given $E = \{1, 2, 3, 4, 5, 6\}$, the even numbers are $2$, $4$, and $6$, so:$$\{x \in E \mid x \text{ is even}\} = \{2, 4, 6\}$$

Ordered Pairs/n-tuples

Definition Ordered Pair/n-tuple

An ordered pair, denoted by $(a, b)$ or $ab$, is a pair of objects where the order matters.
More generally, an ordered n-tuple, denoted $(a_1, a_2, \dots, a_n)$, is a sequence of $n$ elements where the order of the elements is significant.

Remark

The ordered pair $(1, 2)$ is different from the ordered pair $(2, 1)$.

Example

In a sprint relay race, two runners are paired up. Let $L$ be Louis and $H$ be Hugo.
The ordered pair $(L, H)$ means Louis runs first, then passes the baton to Hugo.
The ordered pair $(H, L)$ means Hugo runs first, then passes the baton to Louis.
These are two different races.

Cardinality

Definition Cardinality

$\Card{A}$ denotes the number of elements in the set $A$.

Example

$\Card{\{1,2,3,4,5,6\}}=6=$

Definition Finite and Infinite Sets

A finite set has a finite number of elements. That is, you can count all its elements and finish counting.
An infinite set has an unlimited number of elements; it is not finite.

Example

$\{1, 2, 3\}$ is finite because it has exactly 3 elements.\quad
$\N = \{0, 1, 2, 3, \dots\}$ is infinite because there is no end to counting.

Operations

Intersection and Union

Definition Intersection

The intersection of two sets $A$ and $B$, written $A \cap B$, is the set of elements that are in both $A$ and $B$.

Example

What is the intersection $\{1, 2, 3\} \cap \{2, 3, 4\}$?

Answer

For the intersection $\cap$, include all common element: $\textcolor{colorprop}{2}$ $\textcolor{olive}{3}$. Donc $$\{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3}\} \cap \{ \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\} = \{\textcolor{colorprop}{2},\textcolor{olive}{3}\}$$

Definition Union

The union of two sets $A$ and $B$, written $A \cup B$, is the set of all elements in $A$ or $B$ (or both).

Example

What is the union $\{1, 2, 3\} \cup \{2, 3, 4\}$?

Answer

For the union $\cup$, include all elements from both sets without repeats: $\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}$. So, $$\{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3}\} \cup \{ \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\} = \{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\}$$

Complement

Definition Universal set

A universal set is the set of all elements considered.

Definition Complement

The complement of a set $A$, denoted $A'$, consists of all elements in $U$ that are not in $A$. Sets $A$ and $A'$ are said to be complementary.

Example

Given the universe $U = \{1, 2, 3, 4, 5, 6\}$ and the set $A = \{1, 3, 5\}$, find the complement $A'$.

Answer

Start with the universe $U = \{1, 2, 3, 4, 5, 6\}$.
The set $A = \{1, 3, 5\}$ includes 1, 3, and 5.
The complement $A'$ is all the elements in $U$ that are not in $A$:
$$A' = \{2, 4, 6\}$$

Venn Diagrams

Definition Venn Diagram

A Venn diagram uses a rectangle to show the universal set $U$ and circles to represent other sets within it.

Example

Here’s a Venn diagram for $U = \{1, 2, 3, 4, 5, 6\}$ and $A = \{1, 3, 5\}$: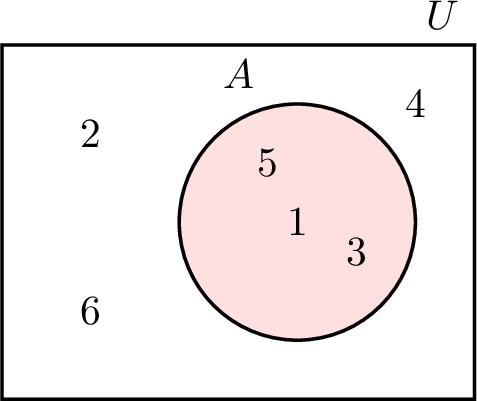

Definition Key Venn Diagram Concepts

This table shows common set operations and their Venn diagrams:

Notation	Meaning	Venn Diagram
$A$	Set $A$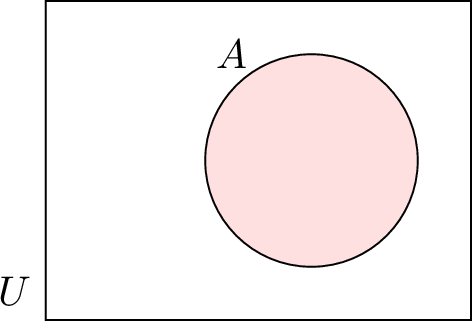
$A'$	Complement of $A$ (everything in $U$ not in $A$)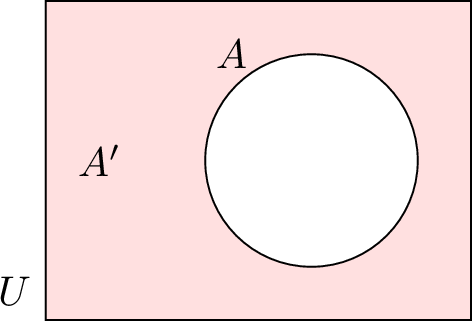
$A \subseteq B$	$A$ is a subset of $B$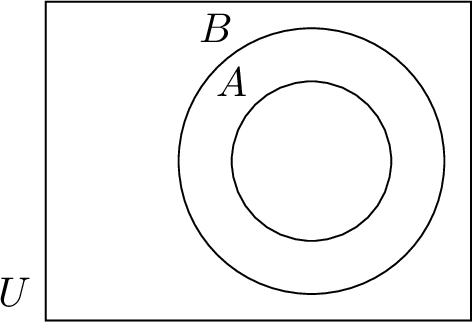
$A \cup B$	Union of $A$ and $B$ (all elements in $A$ or $B$)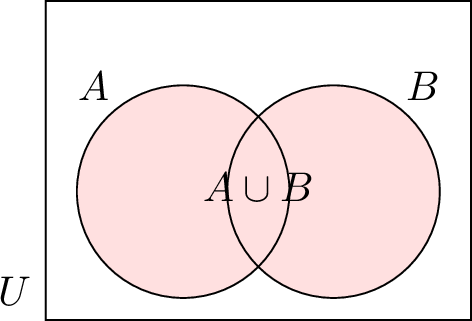
$A \cap B$	Intersection of $A$ and $B$ (elements in both)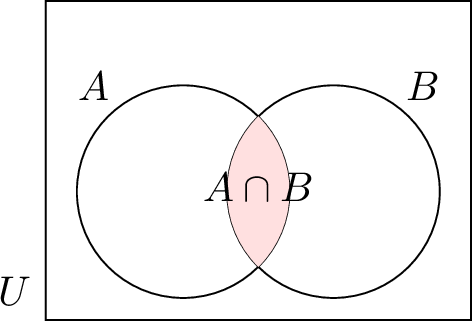
$A \cap B = \emptyset$	$A$ and $B$ are disjoint (no common elements)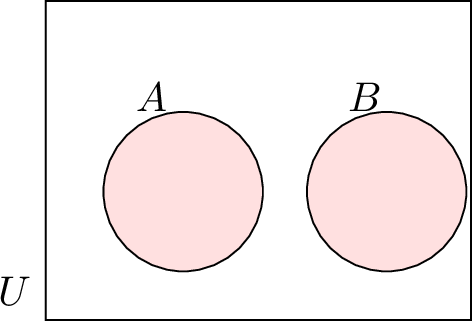

Venn diagrams help solve problems by showing the number of elements in each region.

Definition Counting Elements

In a Venn diagram, we use brackets around numbers to show how many elements are in each region.

Example

Consider this Venn diagram: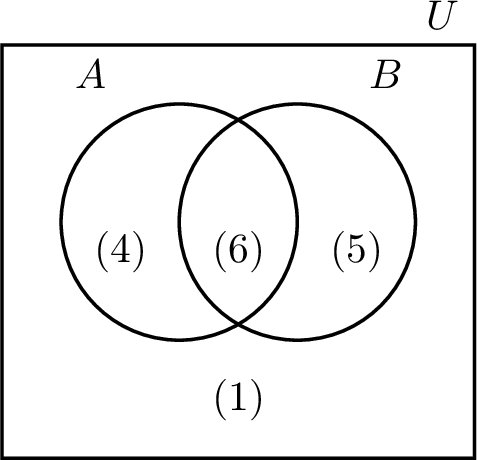

Here, there are 6 elements in both $A$ and $B$, 4 in $A$ but not in $B$, 5 in $B$ but not in $A$, and 1 outside both. Total: $A$ has $4 + 6 = 10$, $B$ has $6 + 5 = 11$.

Number Sets

Number sets are groups of numbers defined by specific properties and form the foundation of mathematics. We begin with the simplest set, the natural numbers ($\N$), used for counting. We then build the integers ($\Z$) by adding negative numbers. Next, we expand to the rational numbers ($\Q$) by allowing fractions, covering all possible divisions between integers. Finally, we reach the real numbers ($\R$) by including irrational numbers, which fills the entire number line. Each set contains the previous ones.

Definition Number Sets

The natural numbers, denoted $\N$, are the counting numbers, starting from zero:$$\N = \{0, 1, 2, 3, 4, 5, 6, \dots\}$$
The integers, denoted $\Z$, include all whole numbers, positive, negative, and zero:$$\Z = \{\dots, -3, -2, -1, 0, 1, 2, 3, \dots\}$$
The rational numbers, denoted $\Q$, are all numbers that can be written as a fraction $\frac{p}{q}$, where $p$ and $q$ are integers and $q \neq 0$:$$\Q = \left\{ \frac{p}{q} \mid p, q \in \Z,\, q \neq 0 \right\}$$
The real numbers, denoted $\R$, include all points on the number line: rational and irrational numbers (such as $\sqrt{2}$ and $\pi$):$$\R = \{\text{all rational and irrational numbers}\}$$

Proposition Relationships Between Number Sets

The number sets are nested as follows:$$\N \subset \Z \subset \Q \subset \R$$This means: every natural number is an integer, every integer is a rational number, and every rational number is a real number.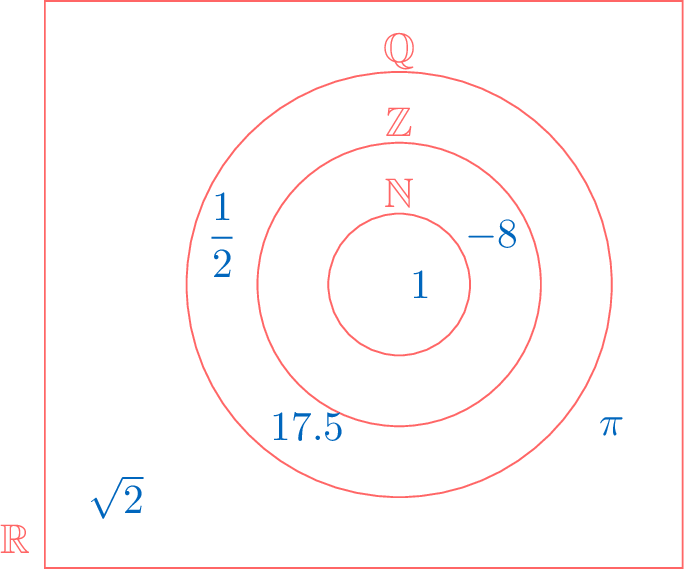

Intervals

Definition Interval

An interval is a set of all real numbers between two endpoints, which may or may not be included in the set.

Example

The set of all real numbers between $0$ and $1$, including $1$ but not $0$, is an interval. It is written as $\{x \in \R \mid 0 < x \leq 1\}$.

Method Representing Intervals on a Number Line

Intervals are often shown on a number line using these conventions:

An \emph{open point} (empty circle) or a parenthesis, means the endpoint is not included.
A \emph{closed point} (filled circle) or a bracket, means the endpoint is included.
An \emph{arrow} shows that the interval extends indefinitely (to $+\infty$ or $-\infty$).

Example

The number line representation of $\{x \in \R \mid 0 < x \leq 1\}$ is:

Definition Interval Notation

Interval Notation	Set-builder notation	Number line representation
$\CloseBracketLeft a, b \CloseBracketRight$	$\{x \in \R \mid a \leqslant x \leqslant b\}$
$\CloseBracketLeft a, b \OpenBracketRight$	$\{x \in \R \mid a \leqslant x < b\}$
$\OpenBracketLeft a, b \CloseBracketRight$	$\{x \in \R \mid a < x \leqslant b\}$
$\OpenBracketLeft a, b \OpenBracketRight$	$\{x \in \R \mid a < x < b\}$
$\CloseBracketLeft a, +\infty\OpenBracketRight $	$\{x \in \R \mid a \leqslant x\}$
$\OpenBracketLeft a, +\infty \OpenBracketRight $	$\{x \in \R \mid a < x\}$
$\OpenBracketLeft -\infty, a\CloseBracketRight$	$\{x \in \R \mid x \leqslant a\}$
$\OpenBracketLeft -\infty, a\OpenBracketRight$	$\{x \in \R \mid x < a\}$

Notation	Meaning	Venn Diagram
\(A\)	Set \(A\)
\(A'\)	Complement of \(A\) (everything in \(U\) not in \(A\))
\(A \subseteq B\)	\(A\) is a subset of \(B\)
\(A \cup B\)	Union of \(A\) and \(B\) (all elements in \(A\) or \(B\))
\(A \cap B\)	Intersection of \(A\) and \(B\) (elements in both)
\(A \cap B = \emptyset\)	\(A\) and \(B\) are disjoint (no common elements)

Interval Notation	Set-builder notation	Number line representation
\(\CloseBracketLeft a, b \CloseBracketRight\)	\(\{x \in \R \mid a \leqslant x \leqslant b\}\)
\(\CloseBracketLeft a, b \OpenBracketRight\)	\(\{x \in \R \mid a \leqslant x < b\}\)
\(\OpenBracketLeft a, b \CloseBracketRight\)	\(\{x \in \R \mid a < x \leqslant b\}\)
\(\OpenBracketLeft a, b \OpenBracketRight\)	\(\{x \in \R \mid a < x < b\}\)
\(\CloseBracketLeft a, +\infty\OpenBracketRight \)	\(\{x \in \R \mid a \leqslant x\}\)
\(\OpenBracketLeft a, +\infty \OpenBracketRight \)	\(\{x \in \R \mid a < x\}\)
\(\OpenBracketLeft -\infty, a\CloseBracketRight\)	\(\{x \in \R \mid x \leqslant a\}\)
\(\OpenBracketLeft -\infty, a\OpenBracketRight\)	\(\{x \in \R \mid x < a\}\)