Long Multiplication
Long multiplication is a systematic method for multiplying numbers, particularly those with multiple digits. It relies on a foundational understanding of single-digit multiplication (times tables) and place value. This chapter will detail the standard algorithm for this procedure.
A Pattern with Tens
To get ready for long multiplication, let's explore a pattern. What happens when we multiply a number by 10, 20, 30, or other multiples of 10?
- 3 groups of 10 (\(3 \times 10\)):
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{3}0\) - 3 groups of 20 (\(3 \times 20\)):
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{6}0\)
- \(3 \times 4 = 12 \quad \rightarrow \quad 3 \times 40 = 120\)
- \(3 \times 5 = 15 \quad \rightarrow \quad 3 \times 50 = 150\)
- \(3 \times 6 = 18 \quad \rightarrow \quad 3 \times 60 = 180\)
Proposition The "Add a Zero" Rule
To multiply by a multiple of 10, you can multiply the non-zero digits first, then place a zero at the end of your answer.\(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}&=\textcolor{olive}{3}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}&=\textcolor{olive}{6 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}&=\textcolor{olive}{9 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}&=\textcolor{olive}{12 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}&=\textcolor{olive}{15 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27 }\\\end{aligned}\) \(\quad \rightarrow \quad\) \(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0&=\textcolor{olive}{3}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0&=\textcolor{olive}{6}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}0&=\textcolor{olive}{9}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}0&=\textcolor{olive}{12}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}0&=\textcolor{olive}{15}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}0&=\textcolor{olive}{18}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}0&=\textcolor{olive}{21}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}0&=\textcolor{olive}{24}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}0&=\textcolor{olive}{27}0\\\end{aligned}\)
Long Multiplication by One-Digit Numbers
The expanded method of multiplication involves calculating partial products for each place value and then summing them. For example, to calculate \(764 \times 2\): 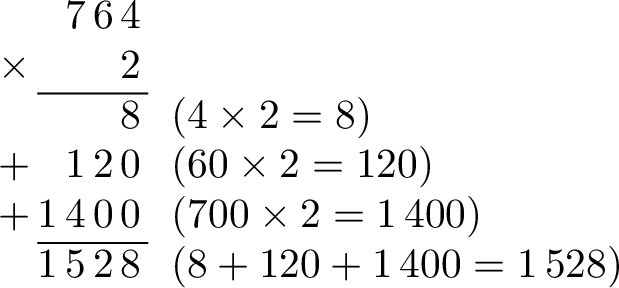
While accurate, this method can be inefficient. The standard algorithm for column multiplication streamlines this process by incorporating a carry-over technique, analogous to that used in column addition.
Method Column Multiplication by a Single Digit
To calculate \(23 \times 7\), the procedure is as follows:
- Step 1: Align the numbers. Position the numbers vertically, aligning them by place value.
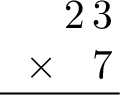
- Step 2: Multiply the ones digit. $$\textcolor{colordef}{3} \text{ ones} \times \textcolor{colordef}{7} \text{ ones} = 21 \text{ ones} = \textcolor{olive}{2} \text{ tens} + \textcolor{colorprop}{1} \text{ one}$$ This result is composed of \(\textcolor{colorprop}{1}\) one and \(\textcolor{olive}{2}\) tens. Write the \(\textcolor{colorprop}{1}\) in the ones column of the result. Carry over the \(\textcolor{olive}{2}\) to the tens column.
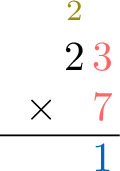
- Step 3: Multiply the tens digit and add the carry-over. $$\textcolor{colordef}{2} \text{ tens} \times \textcolor{colordef}{7} \text{ ones} + \textcolor{olive}{2} \text{ tens (carry-over)} = \textcolor{colorprop}{16} \text{ tens}$$Write \(\textcolor{colorprop}{16}\) in the tens column of the result (no carry because no more calculation).
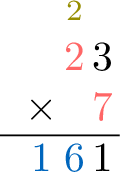
- Result: \(23 \times 7 = 161\).
Long Multiplication by Multi-Digit Numbers
To calculate a product such as \(23 \times 37\), the distributive property is applied. The multiplication is broken into two simpler products:$$\begin{aligned}23 \times 37 &= 23 \times (7 + 30) \\
&= (23 \times 7) + (23 \times 30) \\
&= \textcolor{colorprop}{161} + \textcolor{colordef}{690} \\
&= 851 \end{aligned}$$The column multiplication method organizes this process into a standard algorithm. Note that when multiplying by the tens digit (3), the partial product (\(690\)) is shifted one place to the left. This is indicated by a placeholder zero.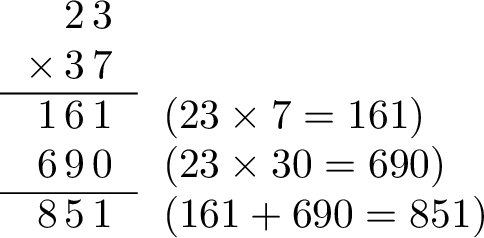
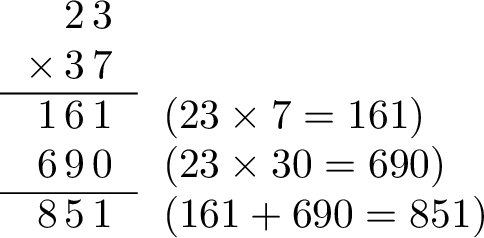
Method Column Multiplication by a Two-Digit Number
To calculate \(23 \times 37\):
- Step 1: Align the numbers vertically by place value.
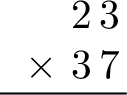
- Step 2: Multiply by the ones digit. Multiply the top number (\(\textcolor{colordef}{23}\)) by the ones digit of the bottom number (\(\textcolor{colordef}{7}\)): \(\textcolor{colordef}{23}\times\textcolor{colordef}{7}=\textcolor{colorprop}{161}\).
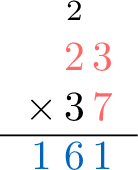
- Step 3: Multiply by the tens digit.
- First, place a placeholder \(\textcolor{olive}{0}\) in the ones column of the second row. This is because we are now multiplying by the tens digit (\(\textcolor{colordef}{3}\), which represents 30). This placeholder shifts our answer one place to the left.
- Next, multiply the top number (23) by the tens digit (\(\textcolor{colordef}{3}\)). Calculate \(\textcolor{colordef}{23}\times\textcolor{colordef}{3}=\textcolor{colorprop}{69}\) and write it to the left of the placeholder.
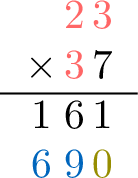
- Step 4: Sum the partial products. Add the results from Step 2 and Step 3: \(\textcolor{colordef}{161}+\textcolor{colordef}{690}=\textcolor{colorprop}{851}\)
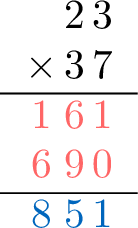
- Result: \(23 \times 37 = 851\).