Time
Time is a big part of our everyday lives! It helps us plan what we do, keep our schedules on track, and remember special moments. Learning about time lets us answer fun and useful questions like:
- What time does my favorite movie start?
- How long will it take to drive to the beach?
- When is the next school holiday?
- When did dinosaurs roam the Earth?
Units of Time
A unit of time is a way to measure how long something takes. We use different units depending on what we’re timing!
Definition Common Units of Time
Here are the units we use most often:
- Seconds (s) – for quick things, like a race.
- Minutes (min) – for short activities, like a break.
- Hours (h) – for longer events, like school.
- Days (d) – for full days, like a weekend.
- Weeks (wk) – for several days, like a vacation.
- Months (mo) – for parts of a year, like summer.
- Years (yr) – for long periods, like your age.
Example
Which unit of time would you use to measure how long it takes to run 100 meters?
We use seconds because running 100 meters is a quick event.
So, the unit is seconds (s).
So, the unit is seconds (s).
Converting Units of Time
Definition Converting Units of Time
To change between units of time, use these facts:
- 1 minute = 60 seconds
- 1 hour = 60 minutes
- 1 day = 24 hours
- 1 week = 7 days

Method How to Convert
- Use multiplication to go from a bigger unit to a smaller one (like minutes to seconds).
- Use division to go from a smaller unit to a bigger one (like minutes to hours).
Example
Convert 2 minutes to seconds.
Since 1 minute = 60 seconds:$$\begin{aligned}[t]2 \, \text{min} &= 2 \times 60 \, \text{s} \\&= 120 \, \text{s}\end{aligned}$$So, 2 minutes is 120 seconds.
Since 1 minute = 60 seconds:$$\begin{aligned}120 \, \text{s} &= 120 \div 60 \, \text{min} \\&= 2 \, \text{min}\end{aligned}$$So, 120 seconds is 2 minutes.
Converting 1 Unit into 2 Units
Method Converting Seconds to Minutes and Seconds
To change seconds into minutes and seconds, divide the total seconds by 60, because 1 minute equals 60 seconds. The number of whole minutes is how many times 60 fits, and any seconds left over stay as seconds.
Example
You run a race in 140 seconds. How many minutes and seconds is that?
- One minute is 60 seconds. Divide 140 by 60 to find the minutes.
- Divide:

- You get 2 minutes, and 20 seconds are left over.
- So, 140 seconds is 2 minutes and 20 seconds: $$ \begin{aligned}[t] 140 \, \text{s} &= (2 \times 60 \, \text{s}) + 20 \, \text{s} \\ &= 2 \, \text{min} + 20 \, \text{s} \end{aligned} $$
24-Hour Time Format
Definition 24-Hour Time Format
The 24-hour time format is a way to tell time without using AM or PM. It counts all 24 hours in a day, from 00:00 (midnight) to 23:59 (almost midnight again).

Example
Write 6:15 PM in 24-hour time.
Since 6:15 PM is 6 hours after noon (12:00):$$\begin{aligned}[t]6:15 \, \text{PM} &= 12 \, \text{h} + 6 \, \text{h} + 15 \, \text{min} \\&= 18 \, \text{h} + 15 \, \text{min} \\&= 18:15\end{aligned}$$So, 6:15 PM is 18:15 in 24-hour time.
Reading Clock
Method Reading Clock
- Hours: The little hand points to the hour. Look at the number it’s on. If it’s between two numbers, choose the smaller one.
- Minutes (by 5s): The big hand points to the minutes. Look at the number it’s on. Each number means 5 minutes. For example: 1 is 5 minutes, 2 is 10 minutes, 3 is 15 minutes, ..., 12 is 0 minutes (o’clock).
- Minutes (by 1s): If the big hand points between numbers, count each small mark after the number. Each mark is 1 minute.
Example
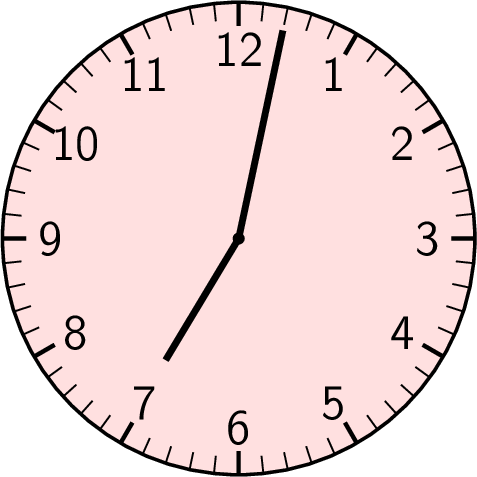
Morning
- The little hand is past the 7 but not yet at the 8, so the hour is 7.
- The big hand is between the 2 and 3. The 2 means \(2\times 5=10\) minutes. Count 2 more marks after the 2: each mark is 1 minute, so 2 marks add 2 minutes.
- Add: 10 minutes + 2 minutes = 12 minutes.
- It’s morning, so the time is 7:12 AM.
Add and Subtract Time
Method Adding Time
Add minutes then hours. If you have too many minutes (more than 60), turn them into hours.
Example
You play a game for 2 hours 30 minutes and read a book for 1 hour 45 minutes. How long is that altogether?
- Add the minutes: 30 minutes + 45 minutes = 75 minutes.
- Too many minutes! 75 minutes is more than 60, so take 60 minutes (1 hour) and keep 15 minutes: 75 min = 1 h 15 min.
- Add the hours: 2 hours + 1 hour + 1 hour (extra hour) = 4 hours.
- So, you spent 4 hours and 15 minutes altogether.
- $$ \begin{aligned}[t] 2 \, \text{h} \, 30 \, \text{min} + 1 \, \text{h} \, 45 \, \text{min} &= (2 \, \text{h} + 1 \, \text{h}) + (30 \, \text{min} + 45 \, \text{min}) \\ &= (2 \, \text{h} + 1 \, \text{h}) + 75 \, \text{min} \\ &= (2 \, \text{h} + 1 \, \text{h}) + (1 \, \text{h} + 15 \, \text{min}) \\ &= 4 \, \text{h} \, 15 \, \text{min} \end{aligned} $$
Method Subtracting Time
Subtract minutes then hours. If you don’t have enough minutes, borrow 1 hour (60 minutes) and add it to the minutes before subtracting.
Example
You have 4 hours 15 minutes of free time. You play a game for 1 hour 45 minutes. How much time is left?
- Subtract the minutes: 15 minutes - 45 minutes. Not enough minutes! Borrow 1 hour (60 minutes) from the 4 hours, leaving 3 hours. Add 60 minutes to 15 minutes: 15 + 60 = 75 minutes.
- Now subtract: 75 minutes - 45 minutes = 30 minutes.
- Subtract the hours: 3 hours - 1 hour = 2 hours.
- So, you have 2 hours and 30 minutes left.
- $$ \begin{aligned}[t] 4 \, \text{h} \, 15 \, \text{min} - 1 \, \text{h} \, 45 \, \text{min} &= 3 \, \text{h} 75 \, \text{min} - 1 \, \text{h}\,20 \, \text{min} \\ &= (3 \, \text{h} - 1 \, \text{h}) + (75 \, \text{min} - 45 \, \text{min}) \\ &= 2 \, \text{h} \, 30 \, \text{min} \\ \end{aligned} $$
Time Problems
Method Solving Time Problems
To solve time problems, you may need to add, subtract, multiply, or divide. Think step-by-step and check your units (like hours or minutes).
Example
You spend 3 hours 30 minutes at school this morning and 2 hours 15 minutes studying this evening. How long is that altogether?
- Add the minutes: 30 minutes + 15 minutes = 45 minutes.
- Add the hours: 3 hours + 2 hours = 5 hours.
- So, you spent 5 hours and 45 minutes altogether.
- $$ \begin{aligned}[t] 3 \, \text{h} \, 30 \, \text{min} + 2 \, \text{h} \, 15 \, \text{min} &= (3 \, \text{h} + 2 \, \text{h}) + (30 \, \text{min} + 15 \, \text{min}) \\ &= 5 \, \text{h} + 45 \, \text{min} \\ &= 5 \, \text{h} \, 45 \, \text{min} \end{aligned} $$
Example
A train starts its journey at 11:20 and arrives at 13:30. How long does the trip take?
- Write the times: Start at 11:20, end at 13:30.
- Subtract minutes: 30 minutes - 20 minutes = 10 minutes.
- Subtract hours: 13 hours - 11 hours = 2 hours.
- The trip takes 2 hours and 10 minutes: $$ \begin{aligned}[t] 13 \, \text{h} \, 30 \, \text{min} - 11 \, \text{h} \, 20 \, \text{min} &= (13 \, \text{h} - 11 \, \text{h}) + (30 \, \text{min} - 20 \, \text{min}) \\ &= 2 \, \text{h} + 10 \, \text{min} \\ &= 2 \, \text{h} \, 10 \, \text{min} \end{aligned} $$
Example
Hugo has to prepare 20 nems for a party. It takes him 2 minutes to make each nem. How long will it take to prepare all the nems?
- Find the total time: 20 nems, and each takes 2 minutes.
- Multiply: \(20 \times 2 = 40\) minutes.
- So, Hugo will need 40 minutes to prepare all the nems.
- $$ \begin{aligned}[t] 20 \times 2 \, \text{min} &= 40 \, \text{min} \end{aligned} $$
Example
You have 1 hour for an exam. Each exercise takes you 4 minutes. How many exercises can you do?
- Change the time to minutes: 1 hour = 60 minutes.
- Divide: 60 minutes ÷ 4 minutes per exercise = 15 exercises.
- So, you can do 15 exercises in 1 hour.
- $$ \begin{aligned}[t] 1 \, \text{h} \div 4 \, \text{min} &=60 \, \text{min} \div 4 \, \text{min}\\ &= 15 \end{aligned} $$
Example
A teacher has 36 minutes to grade tests. Each test takes 3 minutes to grade. How many tests can the teacher grade?
- Find the number of tests: 36 minutes, and each test takes 3 minutes.
- Divide: 36 minutes ÷ 3 minutes per test = 12 tests.
- So, the teacher can grade 12 tests.
- $$ \begin{aligned}[t] 36 \, \text{min} \div 3 \, \text{min per test} &= 12 \end{aligned} $$