Exponents
Exponents are an efficient way of expressing repeated multiplication, and they help us work with large numbers more easily.
Positive Exponents
Imagine you have a chessboard. You place two grains of wheat on the first square, four grains on the second square, eight grains on the third square, and so on, doubling the number of grains on each next square.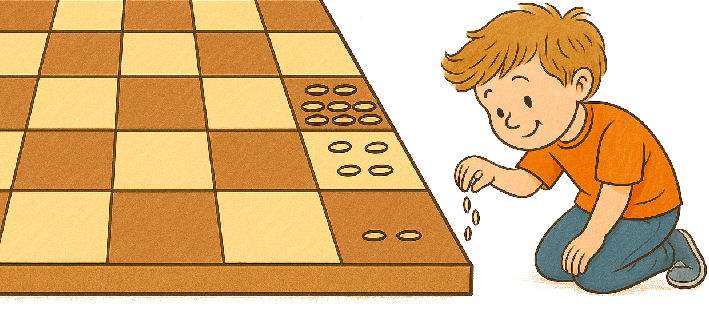

| Square number | Grain number |
| \(1\) | \(2\) |
| \(2\) | \(2 \times 2\) |
| \(3\) | \(2 \times 2 \times 2\) |
| \(\vdots\) | \(\vdots\) |
| \(64\) | \(\overbrace{2 \times 2 \times \dots \times 2}^{64\ \text{factors}}\) |
Definition Exponentiation
Exponentiation is repeated multiplication of a number by itself: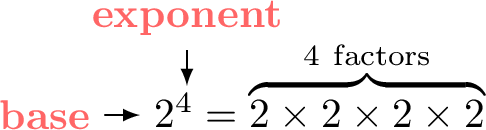
Example
Write using exponent notation: \(5 \times 5 \times 5\)
\(5 \times 5 \times 5 = 5^3\)
Definition Vocabulary
$$\begin{array}{|c|c|c|c|}\hline\text{Value} & \text{Expanded form} & \text{Exponent notation} & \text{Spoken form} \\
\hline2 & 2 & 2^1 & 2\ \text{or}\ 2\ \text{raised to the power}\ 1 \\
4 & 2 \times 2 & 2^2 & 2\ \text{squared or}\ 2\ \text{raised to the power}\ 2 \\
8 & 2 \times 2 \times 2 & 2^3 & 2\ \text{cubed or}\ 2\ \text{raised to the power}\ 3 \\
16 & 2 \times 2 \times 2 \times 2 & 2^4 & 2\ \text{raised to the power}\ 4 \\
32 & 2 \times 2 \times 2 \times 2 \times 2 & 2^5 & 2\ \text{raised to the power}\ 5 \\
\hline\end{array}$$
Example
Find the value for \(2^3\).
$$\begin{aligned}[t]2^3 &= 2 \times 2 \times 2 \\
&= 8\end{aligned}$$
Negative Exponents
To understand negative exponents, let's explore the pattern of multiplying by \(2\):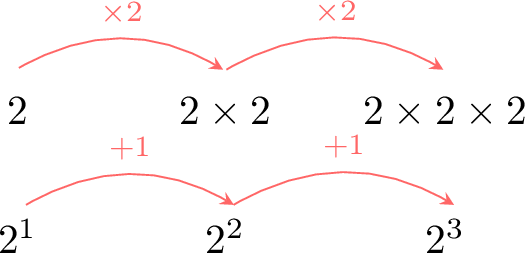


- \(2^1 = 2\)
- \(2^2 = 2 \times 2\)
- \(2^3 = 2 \times 2 \times 2\)

- \(2^0 = 1\)
- \(2^{-1} = \dfrac{1}{2}\)
- \(2^{-2} = \dfrac{1}{2 \times 2}\)
- \(2^{-3} = \dfrac{1}{2 \times 2 \times 2}\)
Definition Exponentiation for a negative exponent
For a negative exponent, exponentiation is repeated division:$$\begin{aligned}[t]a^{-n} &= \dfrac{1}{\underbrace{a \times a \times \dots \times a}_{n\ \text{factors}}} \\
&= \dfrac{1}{a^n} \\
\end{aligned}\qquad \text{and} \qquad a^0=1$$In particular, \(a^{-1} = \dfrac{1}{a}\).
Example
Write \(3^{-2}\) as a fraction.
$$\begin{aligned}[t]3^{-2} &= \dfrac{1}{3 \times 3} \\
&= \dfrac{1}{9}\end{aligned}$$
Rational Exponents
We know about positive exponents, like \(5^3 = 5 \times 5 \times 5\), and also about negative exponents, like \(5^{-3} = \dfrac{1}{5 \times 5 \times 5}\).
But what about fractional exponents?
Using the exponent laws, let's see what happens with \(\textcolor{colordef}{5^{\frac{1}{2}}}\):$$\begin{aligned}\textcolor{colordef}{5^{\frac{1}{2}}} \times \textcolor{colordef}{5^{\frac{1}{2}}} &= 5^{\frac{1}{2}+\frac{1}{2}} \\ &= 5^1 \\ &= \textcolor{olive}{5}\end{aligned}$$And by the definition of the square root: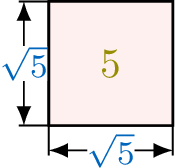
But what about fractional exponents?
Using the exponent laws, let's see what happens with \(\textcolor{colordef}{5^{\frac{1}{2}}}\):$$\begin{aligned}\textcolor{colordef}{5^{\frac{1}{2}}} \times \textcolor{colordef}{5^{\frac{1}{2}}} &= 5^{\frac{1}{2}+\frac{1}{2}} \\ &= 5^1 \\ &= \textcolor{olive}{5}\end{aligned}$$And by the definition of the square root:

Definition Rational exponent
$$\begin{aligned}a^{\frac{1}{2}} &= \sqrt{a} \\
a^{\frac{1}{n}} &= \sqrt[n]{a} \\
a^{\frac{m}{n}} &= \sqrt[n]{a^m}\\
\end{aligned}$$
Exercise
Write \(\sqrt{5}\) in exponent form.
$$\sqrt{5} = 5^{\frac{1}{2}}$$
Exponent Law 1
Let's look at an example:$$\begin{aligned}\textcolor{colordef}{7}^{\textcolor{colorprop}{3}} \times \textcolor{colordef}{7}^{\textcolor{olive}{2}}&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}\,\text{factors}}\times \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{olive}{2}\,\text{factors}} \\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}\,\text{factors}} \\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{3}+\textcolor{olive}{2}} \\
\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and multiplied by the same number raised to the power \(\textcolor{olive}{n}\), that is,$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}},$$the result is equal to \(\textcolor{colordef}{a}\) raised to the sum of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}.$$
Proposition Exponent law 1
$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}$$
$$\begin{aligned}\textcolor{colordef}{a}^{\textcolor{colorprop}{m}} \times \textcolor{colordef}{a}^{\textcolor{olive}{n}}&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}\ \text{factors}}\times \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{olive}{n}\ \text{factors}} \\
&= \overbrace{\textcolor{colordef}{a} \times \cdots \times \textcolor{colordef}{a}}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}\ \text{factors}} \\
&= \textcolor{colordef}{a}^{\textcolor{colorprop}{m}+\textcolor{olive}{n}}\end{aligned}$$
Example
Simplify \(5^2\times 5^4\).
$$\begin{aligned}\textcolor{colordef}{5}^{\textcolor{colorprop}{2}} \times \textcolor{colordef}{5}^{\textcolor{olive}{4}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2}+\textcolor{olive}{4}} \\
&= \textcolor{colordef}{5}^{6}\end{aligned}$$
Exponent Law 2
Let's look at an example:$$\begin{aligned}\dfrac{\textcolor{colordef}{7}^{\textcolor{colorprop}{5}}}{\textcolor{colordef}{7}^{\textcolor{olive}{2}}}&= \dfrac{\overbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5}\,\text{factors}}}{\underbrace{\cancel{\textcolor{colordef}{7}} \times \cancel{\textcolor{colordef}{7}}}_{\textcolor{olive}{2}\,\text{factors}}}\\
&= \overbrace{\textcolor{colordef}{7} \times \textcolor{colordef}{7} \times \textcolor{colordef}{7}}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}\,\text{factors}}\\
&= \textcolor{colordef}{7}^{\textcolor{colorprop}{5} - \textcolor{olive}{2}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\) and divided by the same number raised to the power \(\textcolor{olive}{n}\), that is,$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}$$the result is \(\textcolor{colordef}{a}\) raised to the difference of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}$$
Proposition Exponent Law 2
$$\dfrac{\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}}{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}= \textcolor{colordef}{a}^{\textcolor{colorprop}{m} - \textcolor{olive}{n}}$$
Example
Simplify \(\dfrac{5^7}{5^3}\).
$$\begin{aligned}\dfrac{\textcolor{colordef}{5}^{\textcolor{colorprop}{7}}}{\textcolor{colordef}{5}^{\textcolor{olive}{3}}}&= \textcolor{colordef}{5}^{\textcolor{colorprop}{7} - \textcolor{olive}{3}}\\
&= \textcolor{colordef}{5}^{4}\end{aligned}$$
Exponent Law 3
Let's look at an example:$$\begin{aligned}\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{3}}&= (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})^{\textcolor{olive}{3}} \\
&= \overbrace{(\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}}) \times (\overbrace{\textcolor{colordef}{5}\times \textcolor{colordef}{5}}^{\textcolor{colorprop}{2}\,\text{factors}})}^{\textcolor{olive}{3}\,\text{factors}} \\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} + \textcolor{colorprop}{2} +\textcolor{colorprop}{2}}\\
&= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{3}}\end{aligned}$$In general, when a number \(\textcolor{colordef}{a}\) is raised to the power \(\textcolor{colorprop}{m}\), and that result is raised to the power \(\textcolor{olive}{n}\), that is,$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}},$$the result is \(\textcolor{colordef}{a}\) raised to the product of the exponents:$$\textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}$$
Proposition Exponent Law 3
$$\left(\textcolor{colordef}{a}^{\textcolor{colorprop}{m}}\right)^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{colorprop}{m} \times \textcolor{olive}{n}}$$
Example
Simplify \(\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}}\).
$$\begin{aligned}[t]\left(\textcolor{colordef}{5}^{\textcolor{colorprop}{2}}\right)^{\textcolor{olive}{5}} &= \textcolor{colordef}{5}^{\textcolor{colorprop}{2} \times \textcolor{olive}{5}} \\
&= \textcolor{colordef}{5}^{10}\end{aligned}$$
Exponent Law 4
Let's look at an example:$$\begin{aligned}(\textcolor{colordef}{3} \times \textcolor{colorprop}{5})^{\textcolor{olive}{2}}&= (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \times (\textcolor{colordef}{3} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \times \textcolor{colordef}{3} \times \textcolor{colorprop}{5} \\
&= (\textcolor{colordef}{3} \times \textcolor{colordef}{3}) \times (\textcolor{colorprop}{5} \times \textcolor{colorprop}{5}) \\
&= \textcolor{colordef}{3}^{\textcolor{olive}{2}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{2}}\end{aligned}$$In general, when you multiply two numbers \(\textcolor{colordef}{a}\) and \(\textcolor{colorprop}{b}\), and then raise the product to the power \(\textcolor{olive}{n}\), that is,$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}},$$the result is each factor raised to the power \(\textcolor{olive}{n}\):$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}$$
Proposition Exponent Law 4
$$(\textcolor{colordef}{a}\textcolor{colorprop}{b})^{\textcolor{olive}{n}} = \textcolor{colordef}{a}^{\textcolor{olive}{n}}\, \textcolor{colorprop}{b}^{\textcolor{olive}{n}}$$
Example
Simplify \((\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}}\).
$$(\textcolor{colordef}{2}\times \textcolor{colorprop}{5})^{\textcolor{olive}{3}} = \textcolor{colordef}{2}^{\textcolor{olive}{3}}\, \textcolor{colorprop}{5}^{\textcolor{olive}{3}}$$
Exponent Law 5
Let's look at an example:$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \times \left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right) \\
&= \dfrac{\textcolor{colordef}{5} \times \textcolor{colordef}{5}}{\textcolor{colorprop}{3} \times \textcolor{colorprop}{3}} \\
&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}\end{aligned}$$In general, when a quotient \(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\) is raised to a power \(\textcolor{olive}{n}\), that is,$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}},$$the result is the numerator raised to that power divided by the denominator raised to that power:$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}} = \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}$$
Proposition Exponent Law 5
$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{n}}= \dfrac{\textcolor{colordef}{a}^{\textcolor{olive}{n}}}{\textcolor{colorprop}{b}^{\textcolor{olive}{n}}}$$
Example
Calculate \(\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}\).
$$\begin{aligned}[t]\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}&= \dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}} \\
&= \dfrac{25}{9}\end{aligned}$$
Exponent Law 6
Let's look at an example with a negative exponent:$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{-2}}&= \dfrac{1}{\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{\textcolor{olive}{2}}} \\
&= \dfrac{1}{\dfrac{\textcolor{colordef}{5}^{\textcolor{olive}{2}}}{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}} \\
&= \dfrac{\textcolor{colorprop}{3}^{\textcolor{olive}{2}}}{\textcolor{colordef}{5}^{\textcolor{olive}{2}}} \\
&= \left(\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{5}}\right)^{\textcolor{olive}{2}}\end{aligned}$$In general, when a quotient \(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\) is raised to a negative power \(\textcolor{olive}{-n}\),$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-n}} = \left(\dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}\right)^{\textcolor{olive}{n}}$$
Proposition Exponent Law 6
$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-n}} = \left(\dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}\right)^{\textcolor{olive}{n}}$$and in particular,$$\left(\dfrac{\textcolor{colordef}{a}}{\textcolor{colorprop}{b}}\right)^{\textcolor{olive}{-1}} = \dfrac{\textcolor{colorprop}{b}}{\textcolor{colordef}{a}}$$
Example
Calculate \(\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{-2}\).
$$\begin{aligned}\left(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\right)^{-2} &= \left(\dfrac{\textcolor{colorprop}{3}}{\textcolor{colordef}{5}}\right)^{2} \\
&= \dfrac{3^2}{5^2}\\
&= \dfrac{9}{25} \\
\end{aligned}$$
Order of operations
The order of operations is a set of guidelines that help us solve mathematical expressions in a consistent manner.
Definition Order of Operations
To solve mathematical expressions accurately, we follow the order of operations, which is commonly remembered using the acronym PEMDAS:
- P: Parentheses
- E: Exponents
- M: Multiplication
- D: Division
- A: Addition
- S: Subtraction
Example
Evaluate \((1+2) \times 2^3 + 4\)
$$\begin{aligned}[t](1+2) \times 2^3 + 4 &= \textcolor{colordef}{(1+2)} \times (2^3 + 4 && (\text{parentheses: } \textcolor{colordef}{(1+2)}=3) \\
&= 3 \times \textcolor{colordef}{2^3} + 4 && (\text{exponent: } \textcolor{colordef}{2^3}=8) \\
&= \textcolor{colordef}{3 \times 8} + 4 && (\text{multiplication: } \textcolor{colordef}{3 \times 8}=24) \\
&= \textcolor{colordef}{24 + 4} && (\text{addition: } \textcolor{colordef}{24 + 4}=28 \\
&= 28)\\
\end{aligned}$$
Scientific Notation
Working with very large or very small numbers can be awkward. Since our number system is base ten, we can use powers of ten to rewrite very large or very small numbers to make them easier to work with.
Definition Scientific Notation
A number is expressed in scientific notation when it is written in the form:\(a \times 10^n\) \quad where \(1 \leq a < 10\) and \(n\) is an integer.
Example
Write \(245\) in scientific notation.
$$\begin{aligned}[t]245 &= 2.45 \times 100 \\
&= 2.45 \times 10^2\end{aligned}$$