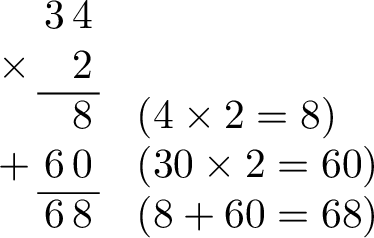Long Multiplication
You are already skilled at using your times tables for single digits. But what happens when you need to multiply bigger numbers, like \(2 \times 34\)?
Long multiplication is a powerful strategy that breaks big problems down into small, easy steps, using the times tables you already know!
Long multiplication is a powerful strategy that breaks big problems down into small, easy steps, using the times tables you already know!
A Pattern with Tens
To get ready for long multiplication, let's explore a pattern. What happens when we multiply a number by 10, 20, 30, or other multiples of 10?
- 3 groups of 10 (\(3 \times 10\)):
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{3}0\) - 3 groups of 20 (\(3 \times 20\)):
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{6}0\)
- \(3 \times 4 = 12 \quad \rightarrow \quad 3 \times 40 = 120\)
- \(3 \times 5 = 15 \quad \rightarrow \quad 3 \times 50 = 150\)
- \(3 \times 6 = 18 \quad \rightarrow \quad 3 \times 60 = 180\)
Proposition The "Add a Zero" Rule
To multiply by a multiple of 10, you can multiply the non-zero digits first, then place a zero at the end of your answer.\(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}&=\textcolor{olive}{3}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}&=\textcolor{olive}{6 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}&=\textcolor{olive}{9 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}&=\textcolor{olive}{12 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}&=\textcolor{olive}{15 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27 }\\\end{aligned}\) \(\quad \rightarrow \quad\) \(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0&=\textcolor{olive}{3}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0&=\textcolor{olive}{6}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}0&=\textcolor{olive}{9}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}0&=\textcolor{olive}{12}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}0&=\textcolor{olive}{15}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}0&=\textcolor{olive}{18}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}0&=\textcolor{olive}{21}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}0&=\textcolor{olive}{24}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}0&=\textcolor{olive}{27}0\\\end{aligned}\)
Multiplying Step-by-Step
How can we solve \(2 \times 34\)? The key is to break 34 into its place values: 30 (tens) and 4 (ones).
\(\quad \rightarrow \quad\) \(\begin{aligned}[t]2 \times 34&=2 \times (30 + 4) \\&=(2 \times 30) + (2 \times 4) \\&=60 + 8\\&=68\\\end{aligned}\)
| \(2 \times 34\) | \(=\) | \(2 \times\) 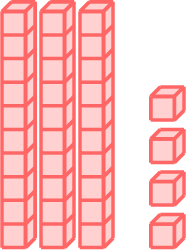 |
| \(=\) | \(2 \times\)  \(+ 2 \times\) \(+ 2 \times\) | |
| \(=\) |  \(+\) \(+\) | |
| \(=\) |  |
Method Long Multiplication by One-Digit Numbers
Calculate:$$34\times 2 $$
- Step 1: Set up the problem. Write the first number on top and the second number below, lining up the place values.
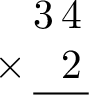
- Step 2: Multiply the ones. Multiply the ones digit of the top number by the bottom number. (\(4 \times 2 = 8\))
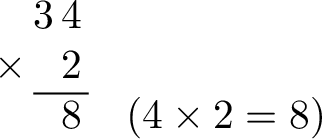
- Step 3: Multiply the tens. Multiply the tens digit of the top number by the bottom number. (\(3 \text{ tens} \times 2 = 6 \text{ tens}\), which is 60).
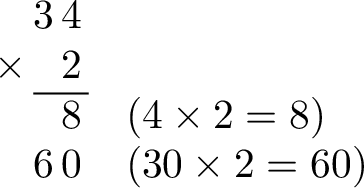
- Step 4: Add the results together. Sum the partial products to find the final answer. (\(8 + 60 = 68\))