Probability
Ever wondered if it'll rain tomorrow or if you'll win a game? That's probability! It's a mathematical way to measure how likely events are to happen.
Sample Spaces
Definition Outcome
An outcome is one possible result of a random experiment.
Example
What are the outcomes when you flip a coin? 
The outcomes are Heads (H)= and Tails (T)=
and Tails (T)= .
.
Example
What are the outcomes when you roll a six-sided die?
The outcomes are 1= ,2=
,2=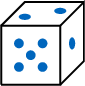 ,3=
,3=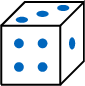 ,4=
,4= ,5=
,5=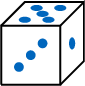 ,and 6=
,and 6=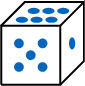 .
.
Definition Sample Space
The sample space is the set of all possible outcomes of a random experiment.
Example
What’s the sample space when you flip a coin?
The sample space is \(\{\)Heads, Tails\(\}=\{\) ,
, \(\}\), or just \(\{\)H, T\(\}\) for short.
\(\}\), or just \(\{\)H, T\(\}\) for short.
Example
What’s the sample space when you roll a six-sided die?
The sample space is \(\{\)1, 2, 3, 4, 5, 6\(\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\).
\(\}\).
Events
Definition Event
An event is a set of outcomes from the outcomes of the sample space. We write it \(E\).
Example
In the experiment of rolling a die, find \(E\) the event of rolling an even number.
Among the outcomes of the sample space \(\{\)1, 2, 3, 4, 5, 6\(\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\) ,the event of rolling an even number is \(E = \{2, 4, 6\}=\{\)
\(\}\) ,the event of rolling an even number is \(E = \{2, 4, 6\}=\{\) ,
, ,
, \(\}\).
\(\}\).
Complementary Events
Ever wonder what happens if you look for everything except a certain event? That’s where the complementary event comes in! It’s just everything in the sample space that isn’t in your event. We usually write it as \(E'\) (“\(E\)-prime”).
Definition Complementary Event
The complementary event of an event \(E\) is all the outcomes in the sample space that are not in \(E\). We write it \(E'\).
Example
In the experiment of rolling a die, let \(E\) the event of rolling an even number. Find \(E'\).
The sample space is \(\{1, 2, 3, 4, 5, 6\}=\{\) ,
, ,
, ,
, ,
, ,
,  \(\}\) and \(E = \{2, 4, 6\}=\{\)
\(\}\) and \(E = \{2, 4, 6\}=\{\) ,
, ,
, \(\}\).
\(\}\).
So \(E'\) is all the other numbers: \(\{1, 3, 5\}=\{\) ,
, ,
, \(\}\). These are the odd numbers.
\(\}\). These are the odd numbers.
So \(E'\) is all the other numbers: \(\{1, 3, 5\}=\{\)
Using Words to Describe Probability
We often use words to talk about probability. If something will never happen, it's impossible. If it will definitely happen, it's certain. In between, we say things like 'likely,' '50-50 chance,' or 'unlikely.' We can line them up from least to most likely.
Definition Probability Line

- Impossible: It can’t happen.
Example: Riding a dinosaur. - Less likely: It probably won’t happen.
Example: Rolling a die and getting a 3. - Even chance: It has the same chance to happen or not.
Example: Tossing a coin and getting head. - Most likely: It will probably happen.
Example: Smiling at school today. - Certain: It will happen.
Example: The sun will rise tomorrow.
Probability
When you flip a coin, there are two possible outcomes: heads or tails. The chance of getting heads is the same as getting tails—it’s 1 out of 2! In math, we write:

Definition Probability
The probability of an event \(E\), written \(P(E)\), is a number that tells us how likely the event is to happen. It's always between 0 (impossible) and 1 (certain).

Example
The probability of an event "even chance" can be represented as:
- Fraction: \( \frac{1}{2} \)
- Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: \( 1 \div 2 = 0.5 \).
- Percentage: To convert the decimal to a percentage, multiply by \(100\pourcent\): \( 0.5 \times 100\pourcent = 50\pourcent \).
Equally Likely
Have you ever flipped a fair coin or rolled a fair die? In these experiments, each outcome is just as likely as the others. We call these equally likely outcomes.
Definition Equally Likely
When all outcomes are equally likely, the probability of an event \(E\) is:$$P(E) = \frac{\text{number of outcomes in the event}}{\text{number of outcomes in the sample space}}$$
Example
What’s the probability of rolling an even number with a fair six-sided die?
- Sample space = \(\{1, 2, 3, 4, 5, 6\}\) (6 outcomes).
- \(E = \{2, 4, 6\}\) (3 outcomes).
- $$\begin{aligned}P(E) &= \frac{3}{6} \\ &= \frac{1}{2}\end{aligned}$$
Complement Rule
Ever wondered how to quickly find the chance that something doesn’t happen? There’s a shortcut for that! It’s called the complement rule.
Proposition Complement Rule
For any event \(E\) and its complementary event \(E'\), the probabilities always add up to \(1\):$$P(E) + P(E') = 1 \quad \text{or} \quad P(E') = 1 - P(E).$$
Example
Farid has a \(0.8\) (80\(\pourcent\)) chance of finishing his homework on time tonight (event \(E\)). What’s the chance he doesn’t finish on time?
The complementary event \(E'\) is “Farid does not finish his homework on time.” By the complement rule:$$\begin{aligned}P(E') &= 1 - P(E) \\
&= 1 - 0.8 \\
&= 0.2\end{aligned}$$So, there’s a \(0.2\) (or 20\(\pourcent\)) chance he doesn’t finish on time!
Experimental Probability
Isaac wishes to determine how a cone lands when tossed—base down or point down? The possible outcomes are as follows:
- Base down:
- Point down:
- Base down: 30 times.
- Point down: 20 times.
- \( P(\text{"base down"}) = \frac{30}{50} = 0.6 \) (60\(\pourcent\)).
- \( P(\text{"point down"}) = \frac{20}{50} = 0.4 \) (40\(\pourcent\)).
Theorem Law of Large Numbers
The probability of an event \(E\) can be estimated using the formula:$$P(E) \approx \frac{\text{number of times the event occurs}}{\text{number of trials}}$$Here, "trials" refer to the number of times the experiment is repeated.