Statistics
Statistical Investigation
Turn on the TV or flip through a newspaper, and you’ll often spot statistics in action. For example:
- Su averages 14.6 points per basketball game.
- Last year was the hottest on record since 1897.
- Scientific Research: Testing if a new medicine works by studying trial results.
- Industrial Production: Improving products by tracking defects and fixing processes.
- Social Issues: Figuring out what people think about new laws through surveys.
- Step 1: State the Problem: Decide what you want to learn.
Example: How has the average temperature changed over the last 100 years? - Step 2: Collect Data: Gather the info you need.
Example: Get temperature records from weather stations. - Step 3: Calculate Descriptive Statistics: Summarize the data with tools like mean, median, or mode.
Example: Find the average temperature for each decade. - Step 4: Organize and Display Data: Put the data in order and show it with charts or graphs.
Example: Make a graph of temperature changes over time. - Step 5: Interpret the Statistics: Figure out what the data tells you.
Example: Does the data show temperatures are rising significantly?
Definition Statistics
Statistics is all about collecting information, sorting it out, summarizing it, and figuring out what it means.
Stating the Problem
When you start a statistical investigation, the first step is to ask a clear question. This keeps you focused on what you’re trying to find out and who or what you’re studying.
We call the group we’re studying the population. It could be all the people in a country, every student in a school, all the animals of a species, or even every item made by a machine. The information we collect from this group is called data, and it can come in many forms—like numbers, words, or measurements.
We call the group we’re studying the population. It could be all the people in a country, every student in a school, all the animals of a species, or even every item made by a machine. The information we collect from this group is called data, and it can come in many forms—like numbers, words, or measurements.
Definition Problem
A problem in statistics is a question that guides us to the information we need to find.
Example
Do girls like math more than boys?
Definition Population
A population is the whole group of people or things with something in common that we want to study.
Example
The population is all the students in a college.
Definition Data
Data is the information we collect, like numbers, words, measurements, or observations.
Example
For our math study, we collect:
- Gender: Is the student a boy or a girl?
- Favorite Subject: What subject do they like best (e.g., Math, Science, English)?
- Math test score: What was their grade on the last assessment??
Definition Types of Variables
- Qualitative Variable (Categorical): Describes categories or groups that cannot be measured numerically.
- Quantitative Variable (Numerical): Represents measurable quantities with numerical values.
Example
For our math study:
- Qualitative Variables: Gender and favorite subject.
- Quantitative Variable: Math test score.
Collecting Data
To collect data, we first decide who or what we’re asking. We can either:
- Do a census: Ask every single member of the population.
- Do a survey: Ask just a part of the population (a sample).
Definition Census
A census means collecting data from everyone in the population.
Definition Survey
A survey means collecting data from a smaller group (sample) of the population.
Example
If you ask every student in the collège about their favorite subject, is it a census or a survey?
It’s a census.
Example
If you only ask the students who are in class math today, is it a census or a survey?
It’s a survey.
Descriptive Statistics
Descriptive statistics are numbers that help us summarize and understand data—like finding the average or the most common answer.
Definition A statistics
A statistics is a single value that sums up or describes a set of data.
Example
The average score in a class is 85\(\pourcent\) is a statistics number because it tells us something about the whole group in one simple figure.
Descriptive Statistics: Relative Frequency
In statistics, it’s important to understand the frequency of a category. This concept helps us analyze patterns and make predictions. It applies to everyday scenarios, such as gauging the popularity of a favorite food among friends or calculating how often a basketball player scores a shot. By studying relative frequencies, we gain valuable insights into data trends.
Definition Frequency and Relative Frequency
Frequency is how many times each value or category appears.
Relative Frequency is the frequency divided by the total, often shown as a percentage.
Relative Frequency is the frequency divided by the total, often shown as a percentage.
Example
The data for favorite subject is: Maths: 15 students, Sciences: 12 students, English: 3 students.
Fill in the table:
Fill in the table:
| Subject | Frequency | Relative frequency (\(\pourcent)\) |
| Maths | ||
| Sciences | ||
| English | ||
| Total | \(100 \pourcent\) |
| Subject | Frequency | Relative frequency (\(\pourcent)\) |
| Maths | 15 | \(\frac{15}{30}\times 100\pourcent = 50\pourcent\) |
| Sciences | 12 | \(\frac{12}{30}\times 100\pourcent = 40\pourcent\) |
| English | 3 | \(\frac{3}{30}\times 100\pourcent = 10\pourcent\) |
| Total | 30 | \(100 \pourcent\) |
Descriptive Statistics: Central Tendency
In statistics, central tendency refers to a measure that identifies a single value as representative of the center or typical point of a dataset. Three key measures are commonly used to assess central tendency: the mode, the mean, and the median.
Definition Mode
The mode is the value that shows up most often in your data.
Example
A group of students reported their last mark (out of 5) on a math exam as follows:$$ 1, 4, 2, 3, 5, 4, 5, 4, 3 $$What is the mode of this dataset?
From the frequency table:
| Mark | Frequency |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 4 |
| 5 | 2 |
Definition Mean
The mean is the average. Add up all the values and divide by how many there are:$$\begin{aligned}\bar{x} &= \frac{\text{sum of all values}}{\text{number of values}} \\&= \frac{x_1 + x_2 + x_3 + \dots + x_n}{n}\end{aligned}$$
Example
Ratings: 1, 4, 2, 3, 5, 4, 5, 4, 4. What’s the mean?
$$\begin{aligned}\text{Mean} &= \frac{1 + 4 + 2 + 3 + 5 + 4 + 5 + 4 + 4}{9} \\&= \frac{32}{9}\\& \approx 3.56\end{aligned}$$
Organizing and Displaying Data
Definition Bar Chart/Histogram
A bar chart/histogram shows data with bars:
- Categories or values go on \(x\)-axis.
- Frequencies go on \(y\)-axis.
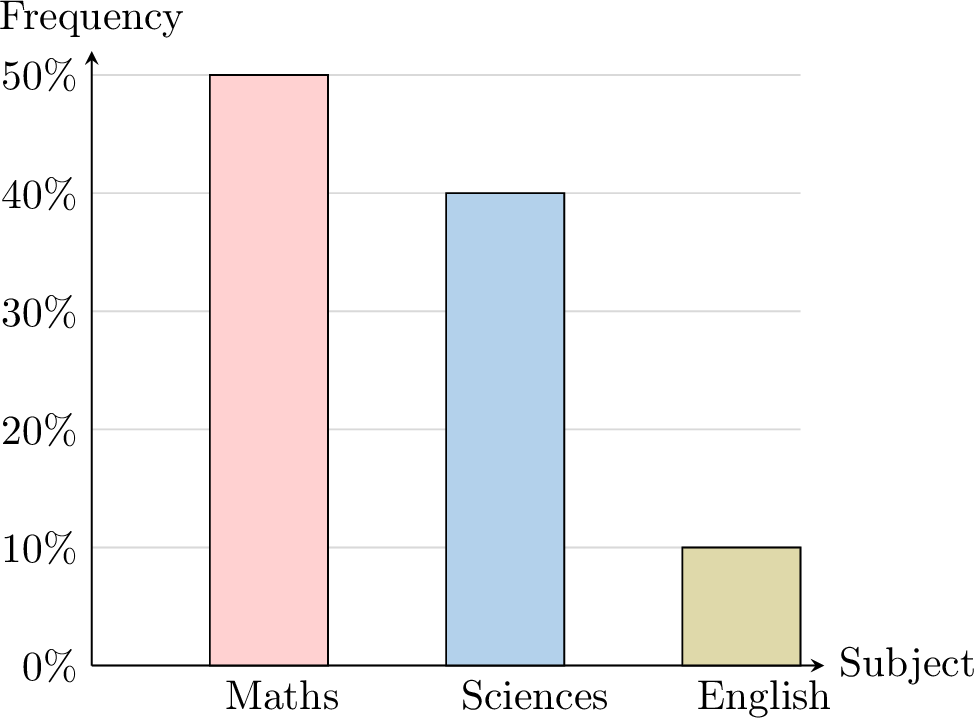
Example
Draw a bar chart for:
| Subject | Relative frequency (\(\pourcent)\) |
| Maths | \(50\pourcent\) |
| Sciences | \( 40\pourcent\) |
| English | \( 10\pourcent\) |
Definition Pie Chart
A pie chart is a circle split into slices to show how data compares.
Example
Draw the pie chart of the following data:
| Subject | Frequency |
| Maths | 15 |
| Sciences | 12 |
| English | 3 |
| Total | 30 |
Angles are :
- Maths : \(\frac{15}{30} \times 360^\circ = 180^\circ\)
- Sciences : \(\frac{12}{30} \times 360^\circ = 144^\circ\)
- English : \(\frac{3}{30} \times 360^\circ = 36^\circ\)

Interpreting the Statistics
Interpreting statistics means looking at the data to find out what it really tells us. We spot patterns, compare groups, and think about what the results mean in real life. The goal? Turn numbers into useful ideas for decisions or advice.
Example
The girls' average score in math is 87 (B+), while the boys' average is 75 (C). Are girls better at math?
Yes, since 87 > 75, on average, girls perform better than boys in math.