Binomial Expansion
In this chapter we study the expansion of powers of a binomial expression such as \((a+b)^n\), where \(n\) is a positive integer.
We will discover patterns in the coefficients using Pascal's triangle, and then state and use the Binomial Theorem.
We will discover patterns in the coefficients using Pascal's triangle, and then state and use the Binomial Theorem.
Binomial Expansion for \(n\equal 2\) and \(n\equal 3\)
Proposition Perfect Squares Expansion
The square of a sum and the square of a difference can be written as:$$(a+b)^2=a^2+2ab+b^2 \quad\text{and}\quad (a-b)^2=a^2-2ab+b^2.$$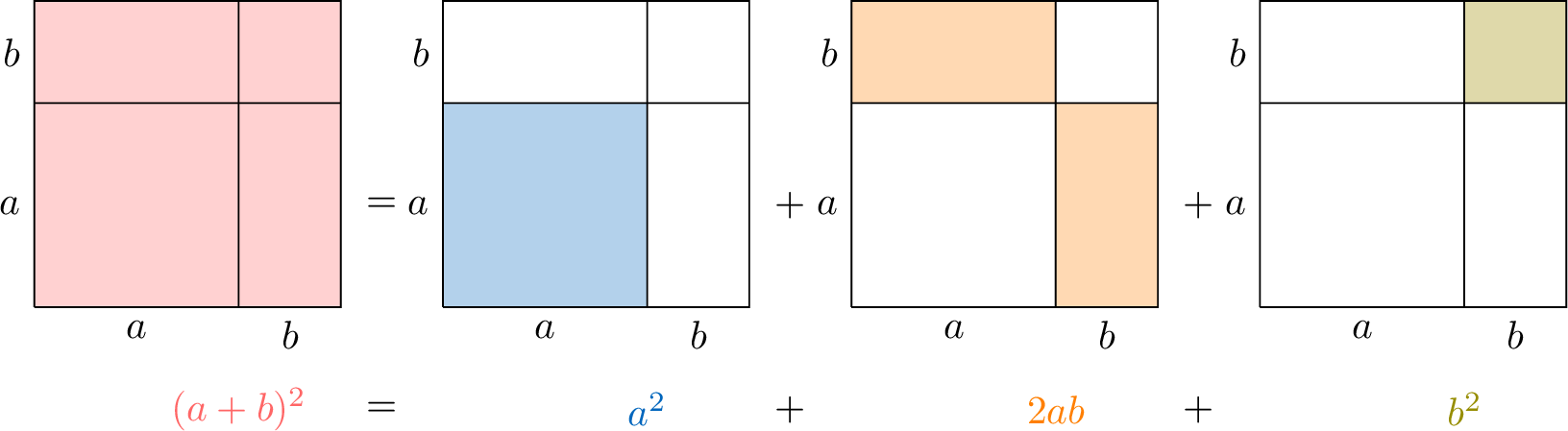
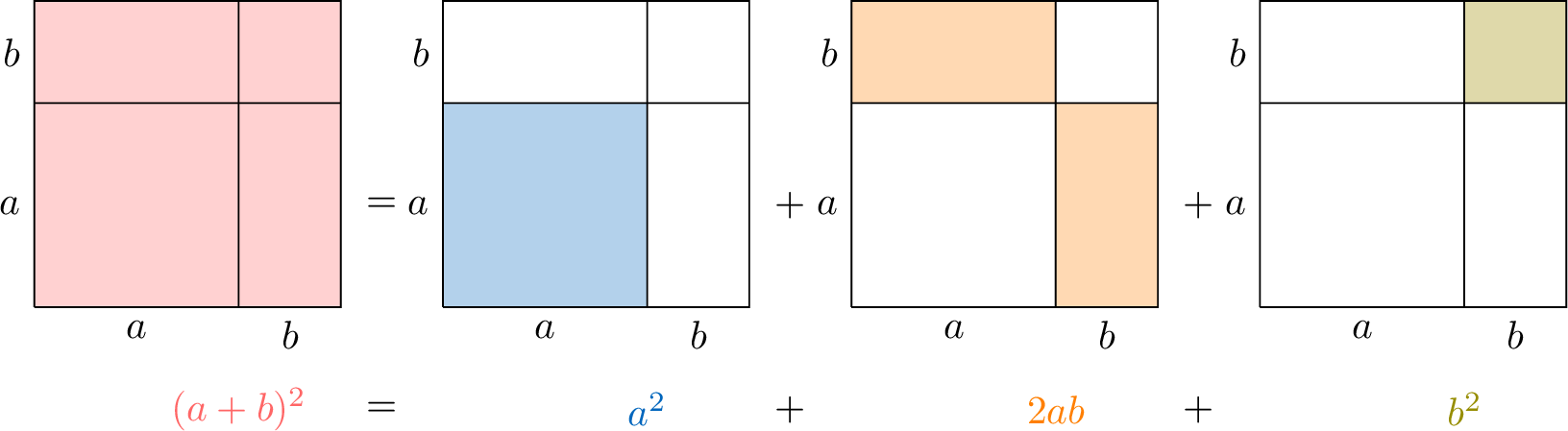
$$\begin{aligned}(a+b)^2 &= (a+b)(a+b) &&\text{(definition of a square)} \\
&= a(a+b)+b(a+b) &&\text{(distributive law)} \\
&= a^2+ab+ab+b^2 &&\text{(expanding)} \\
&= a^2+2ab+b^2 &&\text{(combining like terms)}.\end{aligned}$$Similarly,$$\begin{aligned}(a-b)^2 &= (a-b)(a-b) &&\text{(definition of a square)} \\
&= a(a-b)-b(a-b) &&\text{(distributive law)} \\
&= a^2-ab-ab+b^2 &&\text{(expanding)} \\
&= a^2-2ab+b^2 &&\text{(combining like terms)}.\end{aligned}$$
Example
Expand and simplify \((x+2)^2\).
Using the formula \((a+b)^2=a^2+2ab+b^2\) with \(a=x\) and \(b=2\):$$\begin{aligned}(\textcolor{colordef}{x}+\textcolor{colorprop}{2})^{2} &=\textcolor{colordef}{x}^{2}+2 \times \textcolor{colordef}{x} \times \textcolor{colorprop}{2}+\textcolor{colorprop}{2}^{2} \\
&=x^{2}+4 x+4.\end{aligned}$$So \((x+2)^2=x^2+4x+4\).
Proposition Perfect Cube Expansion
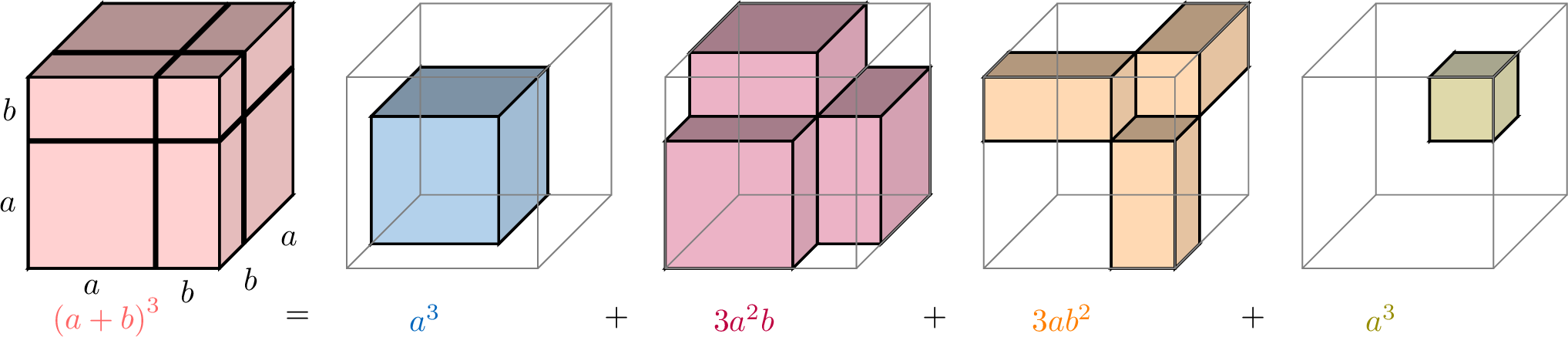
$$\begin{aligned}(a+b)^3 &= (a+b)(a+b)(a+b) &&\text {(cube definition)} \\
&= (a^2+2ab+b^2)(a+b) &&\text {(using the square expansion)} \\
&= (a^2+2ab+b^2)a + (a^2+2ab+b^2)b &&\text {(expanding)} \\
&= a^3+2a^2b+ab^2 + a^2b+2ab^2+b^3 &&\text {(distributive law)} \\
&= a^3+3a^2b+3ab^2+b^3 &&\text {(combining)}\\
\end{aligned}$$
Example
Expand and simplify \((x+2)^3\)
In the perfect cube expansion, we substitute \(a=x\) and \(b=2\):$$\begin{aligned}(\textcolor{colordef}{x}+\textcolor{colorprop}{2})^{3}&= \textcolor{colordef}{x}^{3} + 3 \times \textcolor{colordef}{x}^2 \times \textcolor{colorprop}{2} + 3 \times \textcolor{colordef}{x} \times \textcolor{colorprop}{2}^2 + \textcolor{colorprop}{2}^{3} \\
&= x^{3} + 6x^2 + 12x + 8\end{aligned}$$
Pascal's Triangle
Consider the powers of \((a+b)\):$$\begin{array}{rcccccccccc}(a+b)^1 &=& & & a &+& b\\
(a+b)^2 &=& & 1a^2 &+& 2ab &+& 1b^2\\
(a+b)^3 &=& 1a^3 &+& 3a^2b &+& 3ab^2 &+& 1b^3\\
(a+b)^4 &=& 1a^4 &+& 4a^3b &+& 6a^2b^2 &+& 4ab^3 &+& 1b^4\\
\end{array}$$Now, when we list only the coefficients of the terms, we get Pascal's triangle:$$\begin{array}{ccccccccccc}&&&&1&&1&&&&\text{row 1}\\
&&&1&&2&&1&&&\text{row 2}\\
&&1&&3&&3&&1&&\text{row 3}\\
&1&&4&&6&&4&&1&\text{row 4}\\
\end{array}$$We observe the following pattern.
Definition Pascal's Triangle
- The values at the ends of each row are always \(1\).
- Each interior value is found by adding the two values diagonally above it.
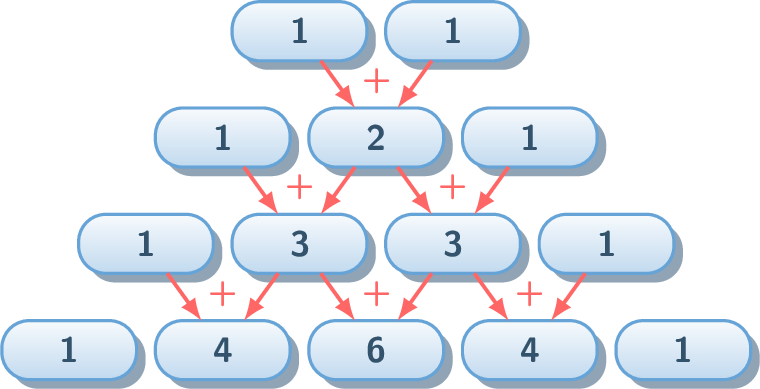
Example
Find the 5th row of Pascal's triangle.
$$\begin{array}{cccccccccccc}&&&&1&&1&&&&&\text{row 1}\\
&&&1&&2&&1&&&&\text{row 2}\\
&&1&&3&&3&&1&&&\text{row 3}\\
&1&&4&&6&&4&&1&&\text{row 4}\\
1&&5&&10&&10&&5&&1&\text{row 5}\end{array}$$So the 5th row is \(1, 5, 10, 10, 5, 1\).
Proposition Binomial Expansion
For the binomial expansion of \((a+b)^n\) where \(n \in \mathbb{N}\):
- As we look from left to right across the expansion, the powers of \(a\) decrease by \(1\), while the powers of \(b\) increase by \(1\).
- The sum of the powers of \(a\) and \(b\) in each term of the expansion is \(n\).
- The number of terms in the expansion is \(n+1\).
- The coefficients of the terms are row \(n\) of Pascal's triangle.
Example
Find the binomial expansion of \((a+b)^5\).
From the 5th row of Pascal's triangle$$\begin{array}{cccccccccccc}&&&&1&&1&&&&&\text{row 1}\\
&&&1&&2&&1&&&&\text{row 2}\\
&&1&&3&&3&&1&&&\text{row 3}\\
&1&&4&&6&&4&&1&&\text{row 4}\\
1&&5&&10&&10&&5&&1&\text{row 5}\end{array}$$we get$$(a+b)^5= a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5.$$
The Binomial Theorem
Definition Factorial
For any positive integer \(n\), \(n!\) (read as "\(n\) factorial") is the product of the first \(n\) positive integers: $$n! = n \times (n-1) \times \dots \times 2 \times 1.$$ By convention, we define \(0! = 1\).
Example
Calculate \(4!\).
\(\begin{aligned}[t]4! &= 4 \times 3 \times 2 \times 1\\ &= 24\end{aligned}\)
Definition Binomial Coefficient
For any integers \(n \geqslant p \geqslant 0\), the binomial coefficient \(\binom{n}{p}\) is defined as $$\binom{n}{p} = \frac{n!}{p!(n-p)!}$$
Proposition Binomial Theorem
For any integer \(n > 0\) and any real numbers \(a,b\in\R\), we have$$(a+b)^n = \binom{n}{0}a^n b^0 + \binom{n}{1}a^{n-1}b^1 + \binom{n}{2}a^{n-2}b^2 + \dotsb + \binom{n}{n}a^0 b^n,$$or more compactly,$$(a+b)^n = \sum_{k=0}^{n} \binom{n}{k}a^{\,n-k}b^{\,k}.$$
We give a combinatorial argument.
Consider the product$$(a+b)^n = \underbrace{(a+b)(a+b)\dotsm(a+b)}_{\text{\(n\) factors}}.$$To obtain a term in the expansion, we choose either \(a\) or \(b\) from each factor and multiply the \(n\) choices together.
A term of the form \(a^{n-k}b^k\) appears whenever we choose \(b\) from exactly \(k\) of the \(n\) brackets (and \(a\) from the remaining \(n-k\) brackets).
The number of such choices is precisely \(\binom{n}{k}\), because we must choose which \(k\) positions will contribute a factor \(b\).
Therefore the coefficient of \(a^{n-k}b^k\) is \(\binom{n}{k}\), and summing over all \(k\) from \(0\) to \(n\) gives$$(a+b)^n = \sum_{k=0}^{n} \binom{n}{k}a^{\,n-k}b^{\,k}.$$
Consider the product$$(a+b)^n = \underbrace{(a+b)(a+b)\dotsm(a+b)}_{\text{\(n\) factors}}.$$To obtain a term in the expansion, we choose either \(a\) or \(b\) from each factor and multiply the \(n\) choices together.
A term of the form \(a^{n-k}b^k\) appears whenever we choose \(b\) from exactly \(k\) of the \(n\) brackets (and \(a\) from the remaining \(n-k\) brackets).
The number of such choices is precisely \(\binom{n}{k}\), because we must choose which \(k\) positions will contribute a factor \(b\).
Therefore the coefficient of \(a^{n-k}b^k\) is \(\binom{n}{k}\), and summing over all \(k\) from \(0\) to \(n\) gives$$(a+b)^n = \sum_{k=0}^{n} \binom{n}{k}a^{\,n-k}b^{\,k}.$$