Radians and the Unit Circle
Radian Measure
The measure of an angle describes what fraction of a full revolution it represents. While degrees (360° in a circle) are a common unit, they are an arbitrary human invention. A more mathematically natural unit is the radian.
Definition Radian Measure
The radian measure of an angle \(\theta\) is defined as the length of the arc it subtends on a unit circle (a circle with radius 1).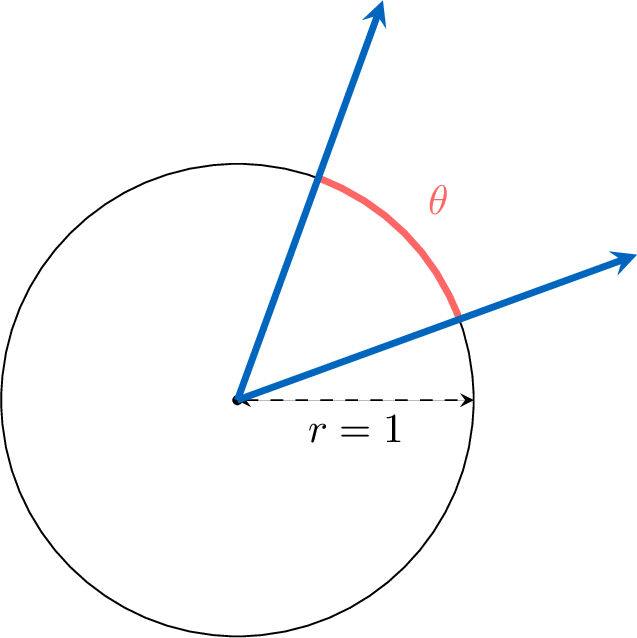

Proposition Angle of a Full Circle
The circumference of a unit circle is \(C = 2\pi(1) = 2\pi\). Therefore, a full circle contains \(2\pi\) radians.
This establishes the fundamental conversion: \(360^\circ = 2\pi\) radians, which simplifies to \(180^\circ = \pi\) radians.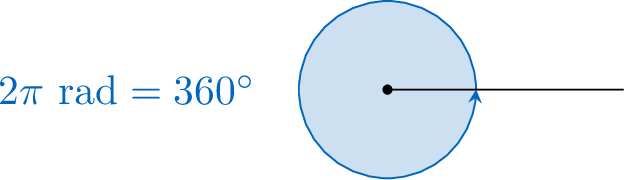
This establishes the fundamental conversion: \(360^\circ = 2\pi\) radians, which simplifies to \(180^\circ = \pi\) radians.

Method Converting Between Degrees and Radians
Based on the relationship \(180^\circ = \pi\) radians:
- To convert from degrees to radians, multiply by \(\dfrac{\pi}{180}\).
- To convert from radians to degrees, multiply by \(\dfrac{180}{\pi}\).
Example
Convert \(60^{\circ}\) to radians.
\(\begin{aligned}[t]60^{\circ}&=60^{\circ} \times \frac{\pi}{180^{\circ}}\\&=\frac{\pi}{3}\end{aligned}\)
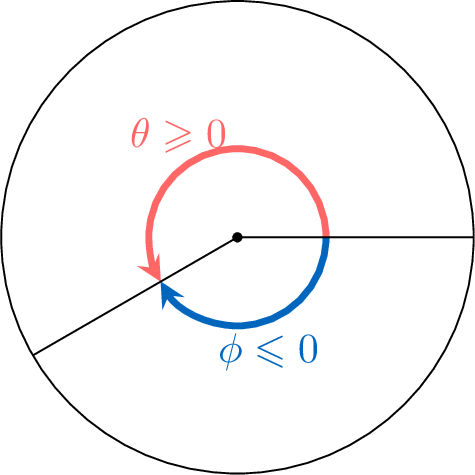
Definition Positive and Negative Angles
- A positive angle measure represents a counterclockwise rotation.
- A negative angle measure represents a clockwise rotation.
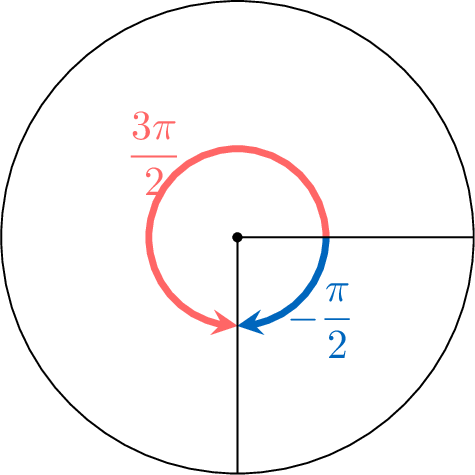
Example
Draw the angles \(\dfrac{3\pi}{2}\) and \(-\dfrac{\pi}{2}\).
Proposition Reference Angles on the Unit Circle
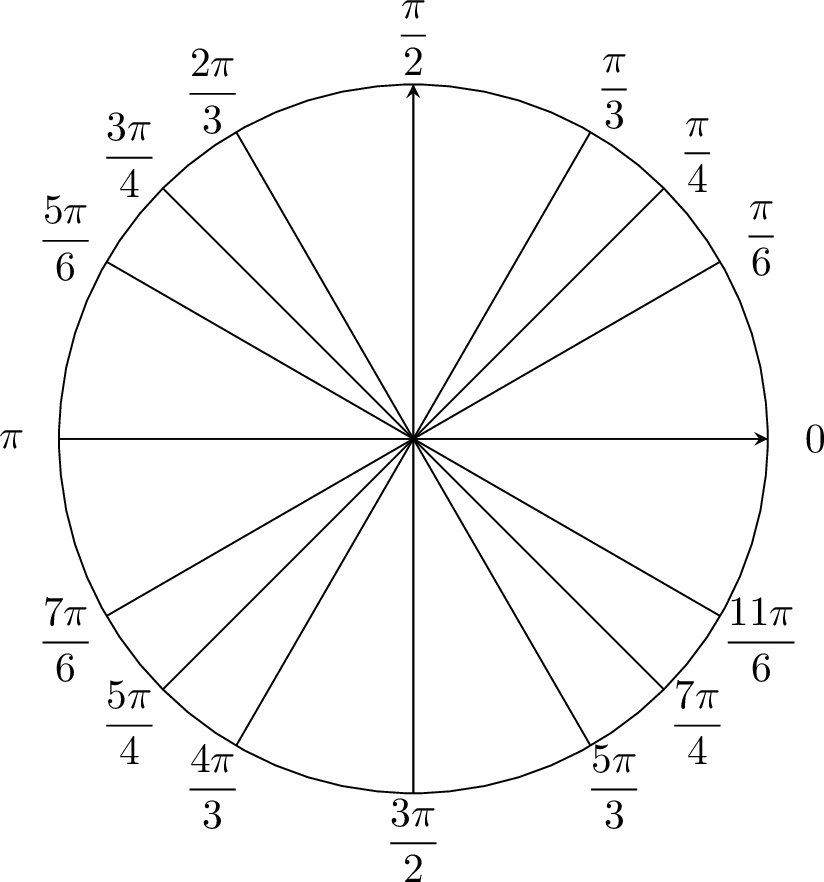
Trigonometry on the Unit Circle
Definition Unit circle
The unit circle is a circle with a radius of 1 centered at the origin.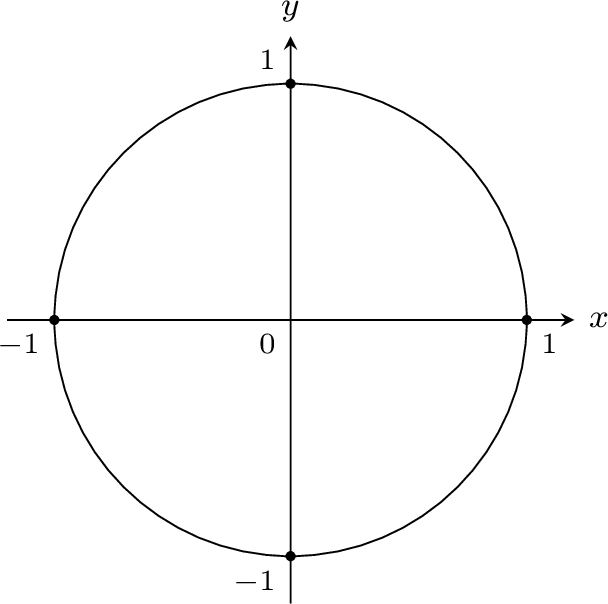

Proposition Relationship between Angle and Coordinates
For any angle \(\theta\), measured counterclockwise from the positive \(x\)-axis, the corresponding point \(M(x,y)\) on the circle defines the values of cosine and sine.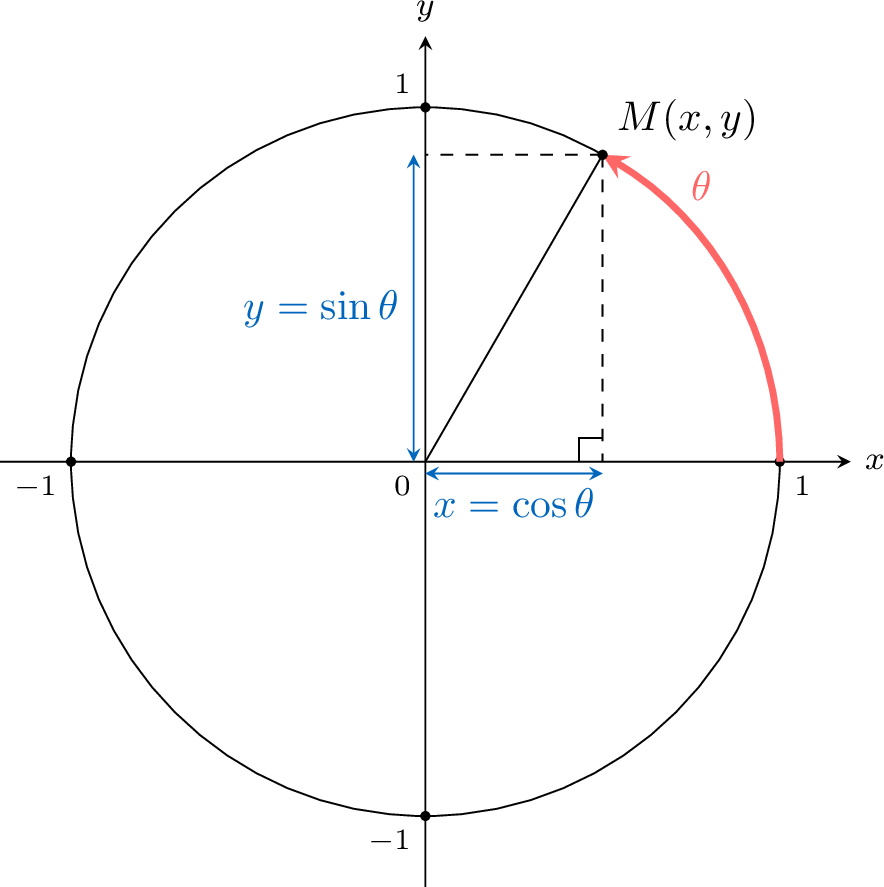
- The \(x\)-coordinate is the cosine of the angle: \(\cos \theta = x\)
- The \(y\)-coordinate is the sine of the angle: \(\sin \theta = y\)

Example
Find the values \(\cos \left(\dfrac{\pi}{2}\right)\) and \(\sin \left(\dfrac{\pi}{2}\right)\).
On the unit circle, the point corresponding to the angle \(\dfrac{\pi}{2}\) has coordinates \((0,1)\):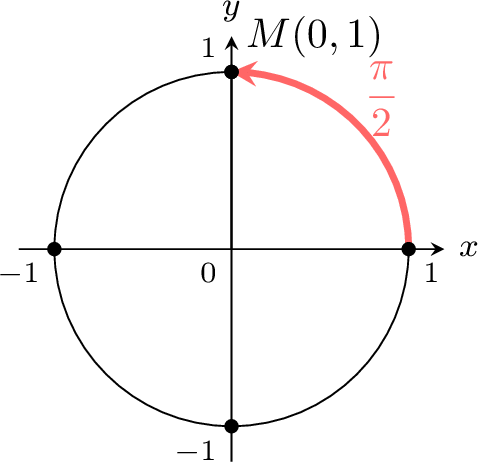
\(\sin \left(\dfrac{\pi}{2}\right)=1 \quad\) \(y\)-coordinate
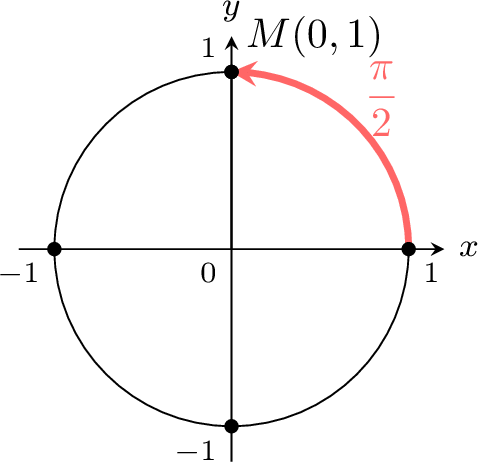
\(\sin \left(\dfrac{\pi}{2}\right)=1 \quad\) \(y\)-coordinate
Proposition Sign of Sine and Cosine
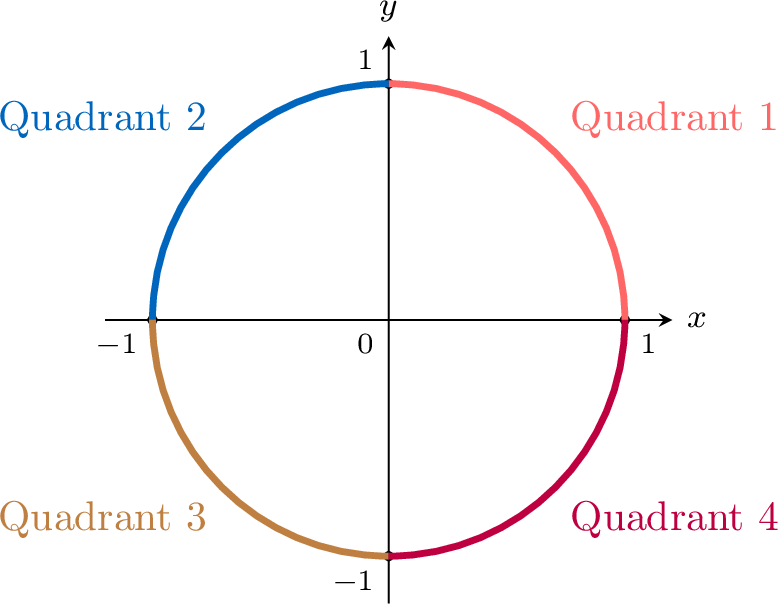
| Quadrant | \(\cos \theta\) | \(\sin \theta\) |
| 1 | \(+\) | \(+\) |
| 2 | \(-\) | \(+\) |
| 3 | \(-\) | \(-\) |
| 4 | \(+\) | \(-\) |
Trigonometric Identities
Proposition Pythagorean Identity
For any angle \(\theta\):$$ \cos^2 \theta + \sin^2 \theta = 1 $$
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).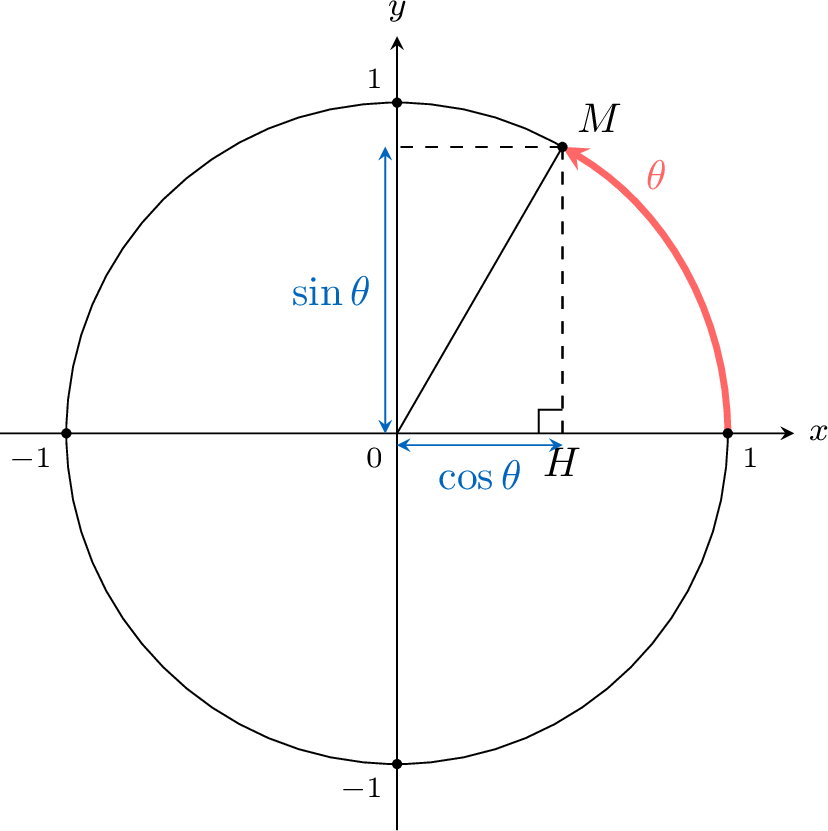

Proposition Maximum and Minimum of Trigonometric Ratios
$$-1 \leqslant \cos \theta \leqslant 1\quad\text{ and }\quad-1 \leqslant \sin \theta \leqslant 1$$
- Geometric proof:

- Analytical proof (for cosine; the proof for sine is analogous):$$\begin{aligned}0 &\leqslant \sin ^2 \theta &&\text{(a square is always non-negative)} \\ \cos ^2 \theta &\leqslant \cos ^2 \theta +\sin ^2 \theta &&\text{(add } \cos ^2 \theta\text{ to both sides)} \\ \cos ^2 \theta &\leqslant 1 &&(\cos ^2 \theta+\sin ^2 \theta=1) \\ |\cos \theta| &\leqslant 1 &&\text{(taking square roots)} \\ -1 &\leqslant \cos \theta \leqslant 1 &&\end{aligned}$$The same reasoning applied to \(\sin \theta\) gives \(-1 \leqslant \sin \theta \leqslant 1\).
Proposition Periodicity Identity
For any angle \(\theta\) and any integer \(k\):$$ \cos(\theta + 2k\pi) = \cos\theta \quad \text{and} \quad \sin(\theta + 2k\pi) = \sin\theta $$
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\theta+2\pi),\sin(\theta+2\pi))\) be the point on the unit circle at the angle \(\theta+2\pi\).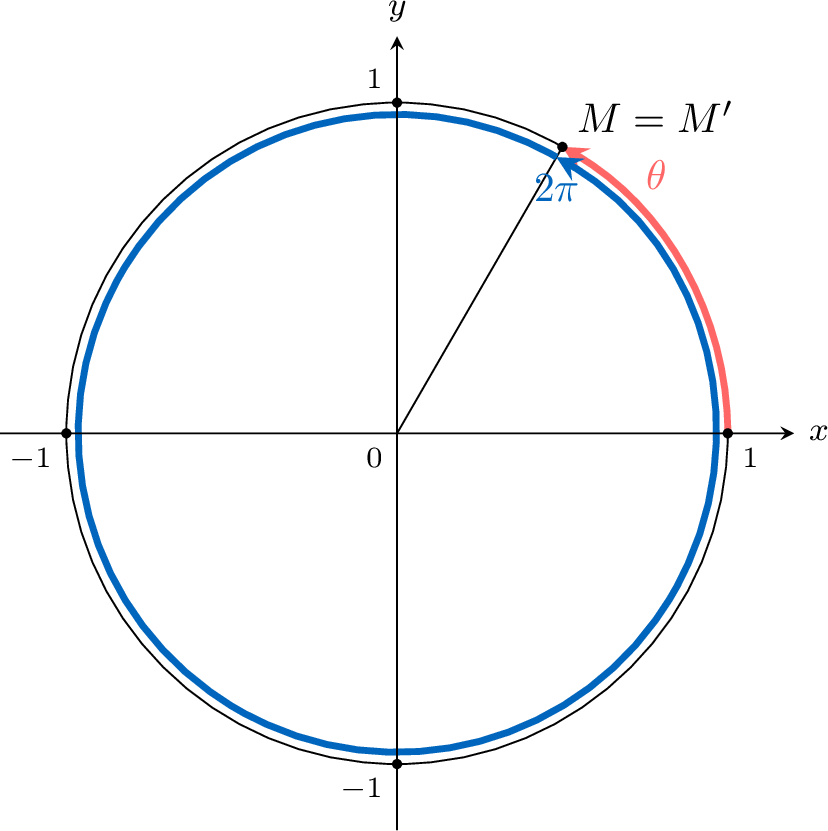
Thus, \(\cos (\theta+2 \pi)=\cos \theta\) and \(\sin (\theta+2 \pi)=\sin \theta\).
The same argument holds for any multiple of \(2\pi\), i.e. for any integer \(k\).
Let \(M'(\cos(\theta+2\pi),\sin(\theta+2\pi))\) be the point on the unit circle at the angle \(\theta+2\pi\).

Thus, \(\cos (\theta+2 \pi)=\cos \theta\) and \(\sin (\theta+2 \pi)=\sin \theta\).
The same argument holds for any multiple of \(2\pi\), i.e. for any integer \(k\).
Proposition Add \(\pi\) to Trigonometric Ratios
Reflection through the origin:$$\begin{aligned}\sin (\pi+\theta)&=-\sin \theta \\
\cos (\pi+\theta)&=-\cos \theta\end{aligned}$$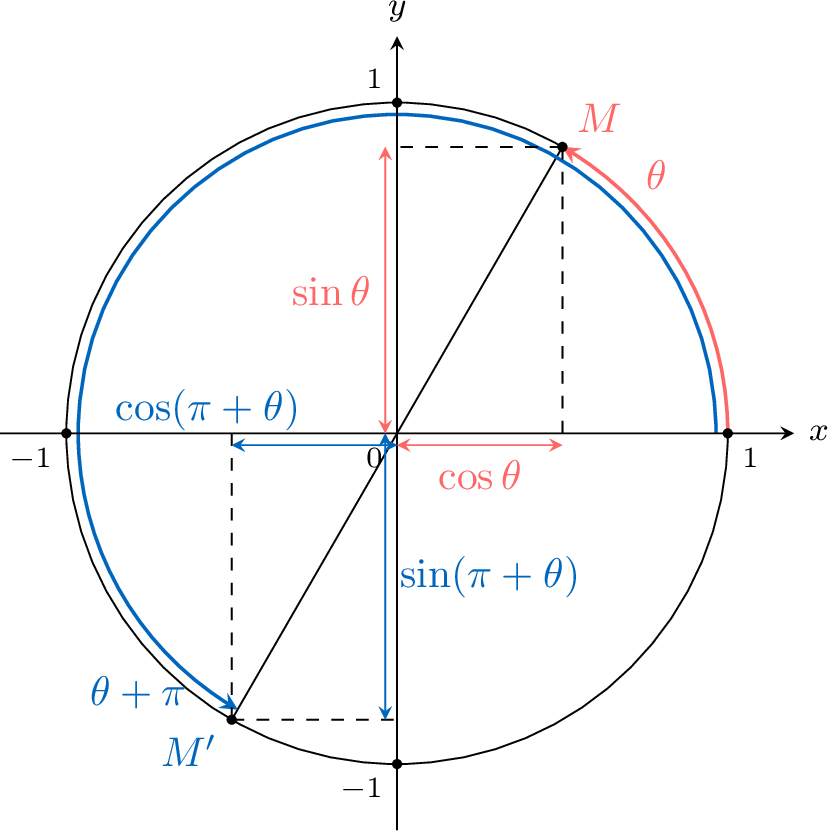

Let \(\theta\) be an angle.
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\pi+\theta),\sin(\pi+\theta))\) be the point on the unit circle at the angle \(\pi+\theta\).
A rotation by an angle \(\pi\) is a half-turn about the origin \(O\), which is the same as a point reflection through \(O\). Therefore, the coordinates of \(M'\) are the opposites of the coordinates of \(M\).
So\(\begin{aligned}[t]\sin (\pi+\theta)&=-\sin \theta \\\cos (\pi+\theta)&=-\cos \theta\end{aligned}\)
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\pi+\theta),\sin(\pi+\theta))\) be the point on the unit circle at the angle \(\pi+\theta\).
A rotation by an angle \(\pi\) is a half-turn about the origin \(O\), which is the same as a point reflection through \(O\). Therefore, the coordinates of \(M'\) are the opposites of the coordinates of \(M\).
So\(\begin{aligned}[t]\sin (\pi+\theta)&=-\sin \theta \\\cos (\pi+\theta)&=-\cos \theta\end{aligned}\)
Proposition Opposite of Trigonometric Ratios
Reflection in the \(x\)-axis:$$\begin{aligned}\sin (-\theta)&=-\sin \theta \\
\cos (-\theta)&=\cos \theta\end{aligned}$$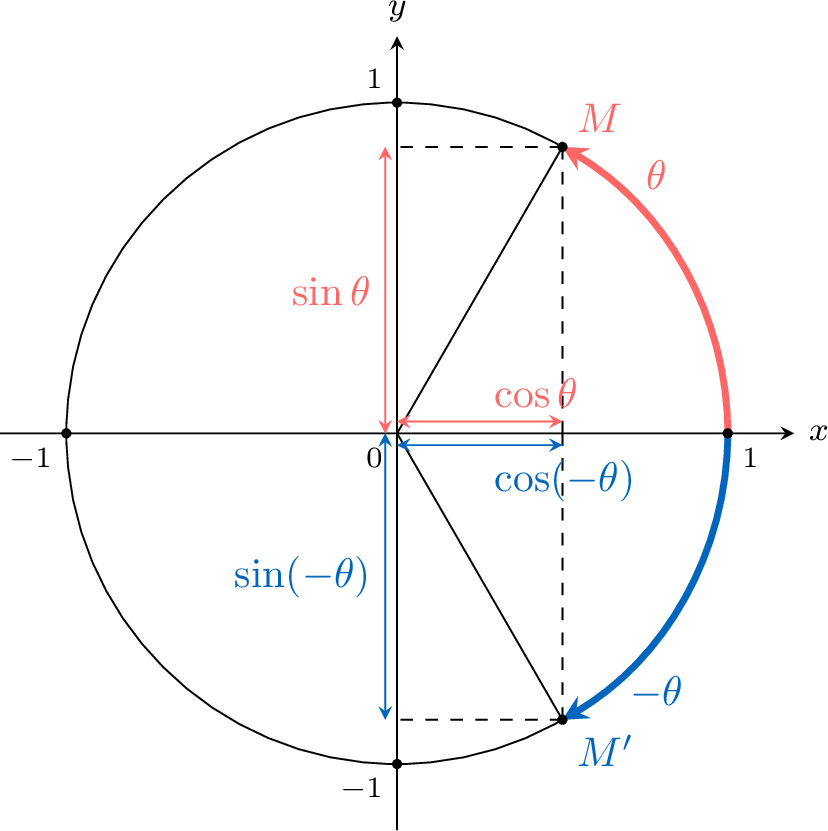

Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(-\theta),\sin(-\theta))\) be the point on the unit circle at the angle \(-\theta\).
The point \(M'\) is the reflection of \(M\) across the \(x\)-axis. Therefore, the \(x\)-coordinate of \(M'\) is the same as that of \(M\), and the \(y\)-coordinate of \(M'\) is the opposite of the \(y\)-coordinate of \(M\).
So\(\begin{aligned}[t]\sin (-\theta)&=-\sin \theta \\\cos (-\theta)&=\cos \theta\end{aligned}\)
Let \(M'(\cos(-\theta),\sin(-\theta))\) be the point on the unit circle at the angle \(-\theta\).
The point \(M'\) is the reflection of \(M\) across the \(x\)-axis. Therefore, the \(x\)-coordinate of \(M'\) is the same as that of \(M\), and the \(y\)-coordinate of \(M'\) is the opposite of the \(y\)-coordinate of \(M\).
So\(\begin{aligned}[t]\sin (-\theta)&=-\sin \theta \\\cos (-\theta)&=\cos \theta\end{aligned}\)
Proposition Identities with \(\frac{\pi}{2} - \theta\)
Reflection across the line \(y=x\): $$\begin{aligned}\cos\left(\frac \pi 2 -\theta\right) &= \sin \theta \\
\sin\left(\frac \pi 2 -\theta\right) &= \cos \theta \\
\end{aligned}$$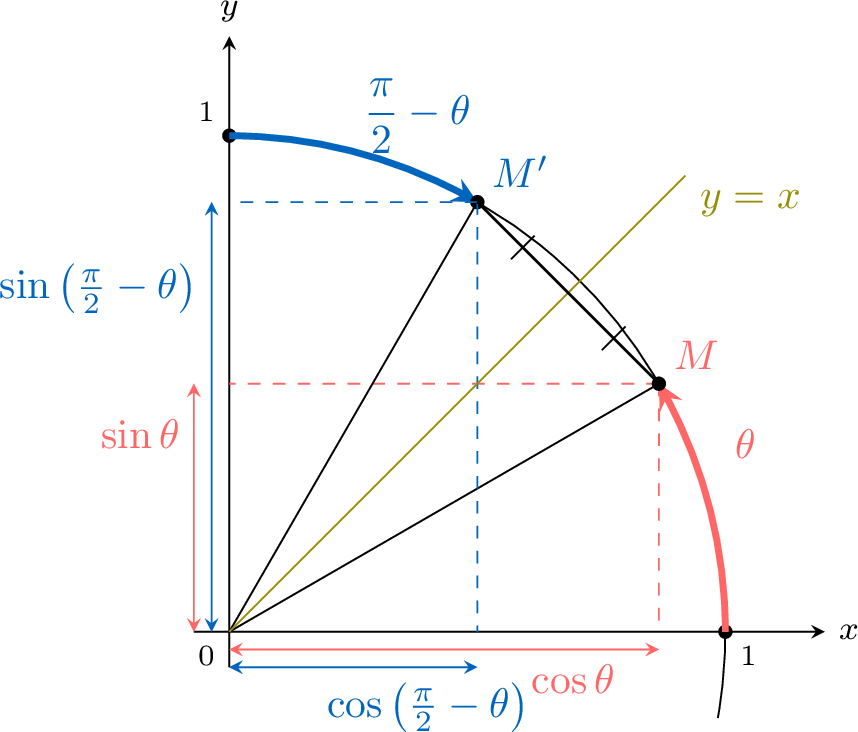

Let \(\theta\) be an angle.
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\frac \pi 2 -\theta),\sin(\frac \pi 2 -\theta))\) be the point on the unit circle at the angle \(\frac \pi 2 -\theta\).
The points \(M\) and \(M'\) are symmetric with respect to the line \(y=x\), so the \(x\)-coordinate of \(M\) is the \(y\)-coordinate of \(M'\), and the \(y\)-coordinate of \(M\) is the \(x\)-coordinate of \(M'\).
So\(\begin{aligned}[t]\cos\left(\frac \pi 2 -\theta\right) &= \sin \theta \\\sin\left(\frac \pi 2 -\theta\right) &= \cos \theta \\\end{aligned}\)
Let \(M(\cos \theta,\sin\theta)\) be the point on the unit circle at the angle \(\theta\).
Let \(M'(\cos(\frac \pi 2 -\theta),\sin(\frac \pi 2 -\theta))\) be the point on the unit circle at the angle \(\frac \pi 2 -\theta\).
The points \(M\) and \(M'\) are symmetric with respect to the line \(y=x\), so the \(x\)-coordinate of \(M\) is the \(y\)-coordinate of \(M'\), and the \(y\)-coordinate of \(M\) is the \(x\)-coordinate of \(M'\).
So\(\begin{aligned}[t]\cos\left(\frac \pi 2 -\theta\right) &= \sin \theta \\\sin\left(\frac \pi 2 -\theta\right) &= \cos \theta \\\end{aligned}\)
Multiples of \(\frac{\pi}{4}\)
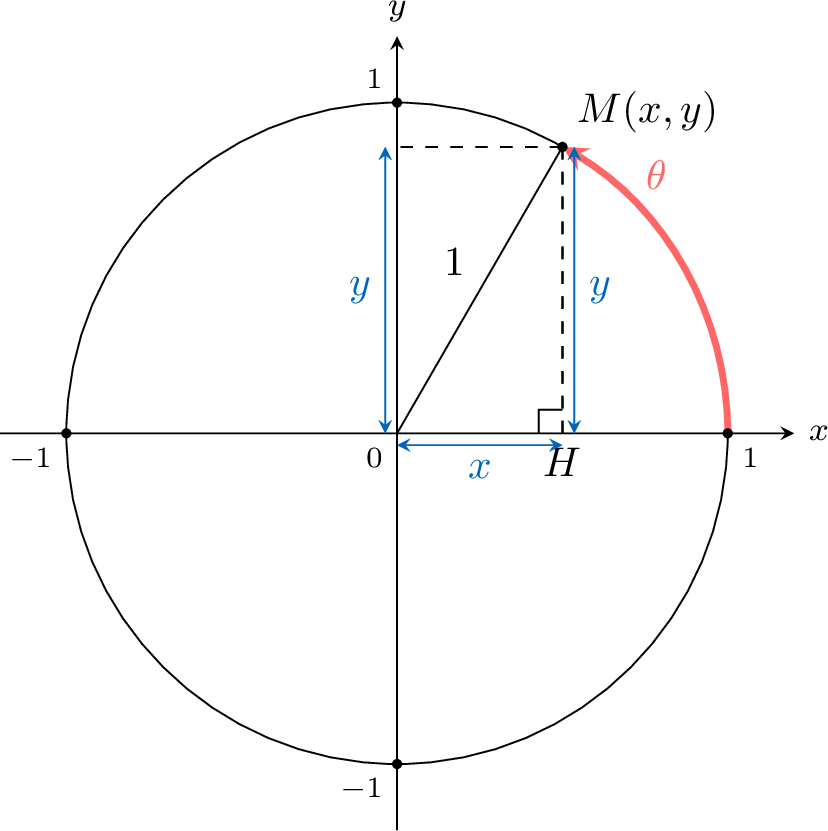
Proposition Coordinates for Angle \(\frac{\pi}{4}\)
$$\cos \frac{\pi}{4}=\frac{\sqrt{2}}{2} \quad \text { and } \quad \sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}$$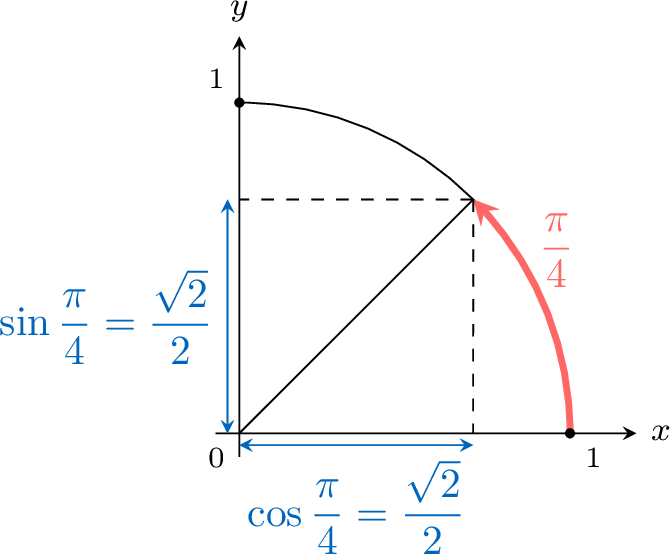
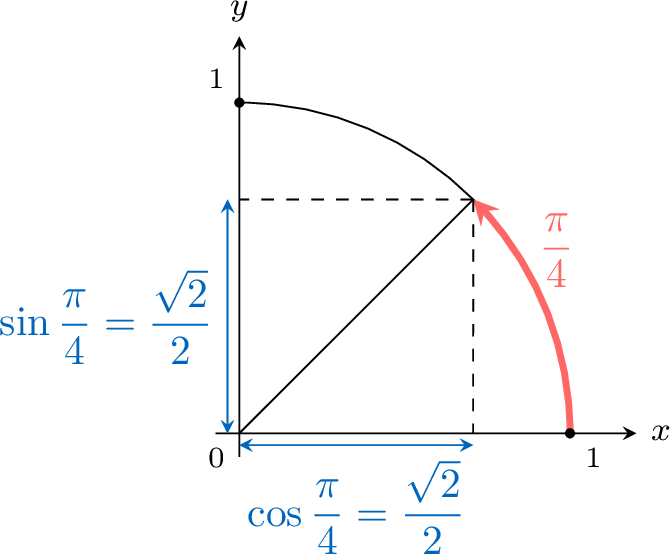
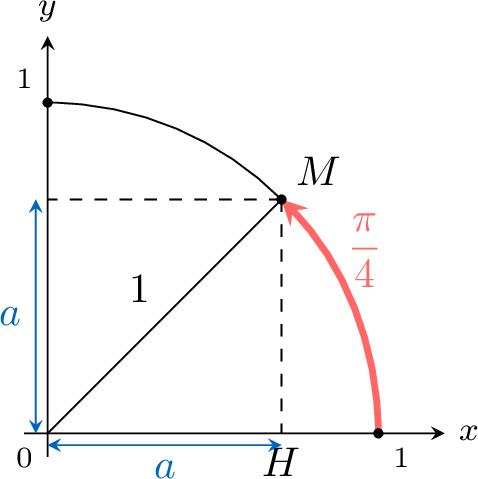
Since \(\angle{OMH}=\angle{MOH}\), the triangle \(OHM\) is isosceles.
Let \(a=OH=HM\).$$\begin{aligned} a^2+a^2 &=1^2 \quad \text { (Pythagorean theorem in the right triangle } OHM)\\ 2 a^2 &=1 \\ a^2 &=\frac{1}{2} \\ a &=\frac{\sqrt{2}}{2} \quad \text { since } a\geqslant 0\end{aligned}$$So \(M\left(\dfrac{\sqrt{2}}{2},\dfrac{\sqrt{2}}{2}\right)\).
As \(\cos \theta\) is the \(x\)-coordinate of \(M\) and \(\sin \theta\) is the \(y\)-coordinate of \(M\),$$\cos \frac{\pi}{4}=\frac{\sqrt{2}}{2} \quad \text { and } \quad \sin \frac{\pi}{4}=\frac{\sqrt{2}}{2}$$
Proposition Multiples of \(\frac{\pi}{4}\)
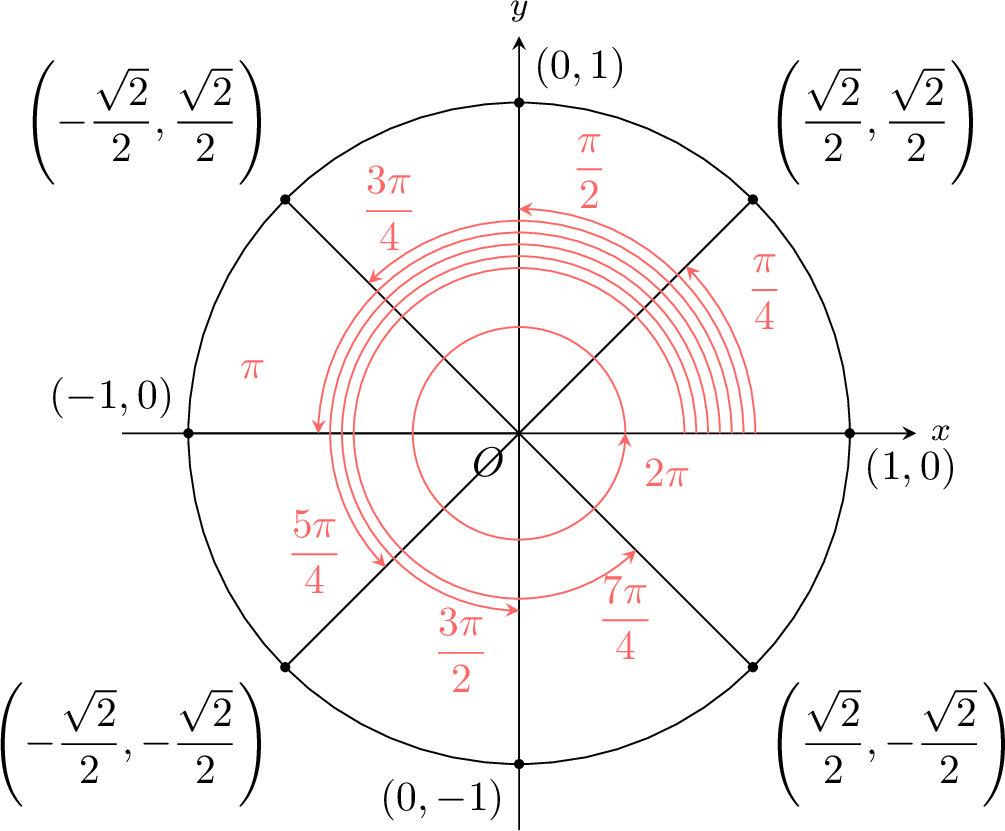
The coordinates of each point are found by using reflection symmetries over the axes or the origin.
The signs of the coordinates are determined by the quadrant in which the angle lies.
Example
Find \(\cos \dfrac{3 \pi}{4}\).
\(\cos \dfrac{3 \pi}{4} = -\dfrac{\sqrt{2}}{2}\)
Multiples of \(\frac{\pi}{6}\)
Proposition Coordinates of Angle \(\frac{\pi}{3}\)
$$\cos \frac{\pi}{3}=\frac{1}{2} \quad \text { and } \quad \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$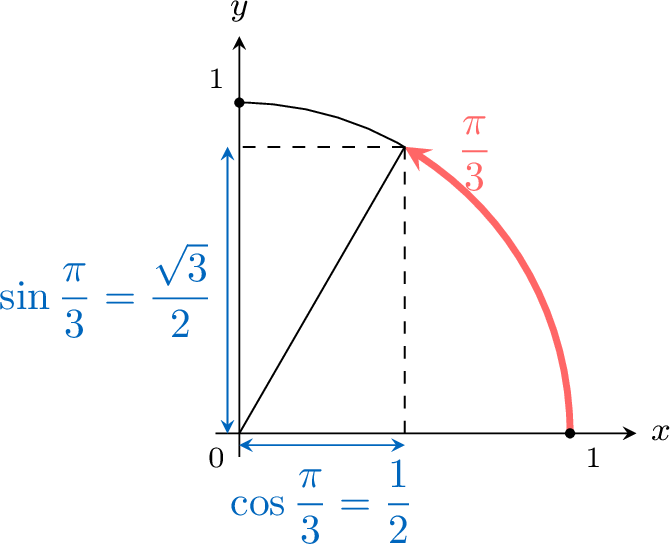
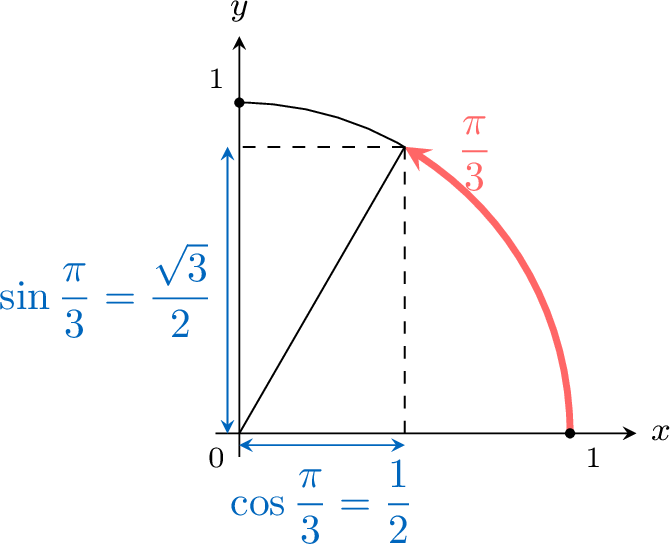
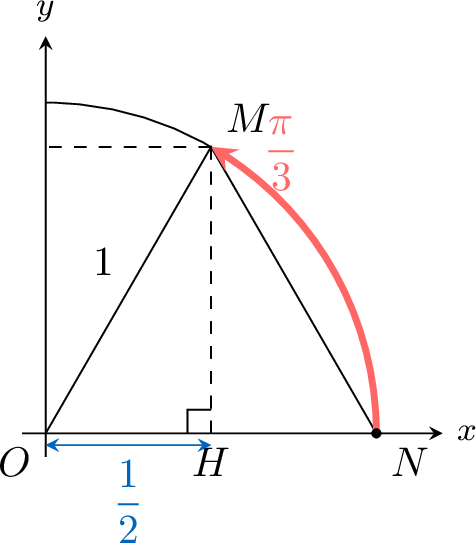
As \(ON=OM=1\), the triangle \(OMN\) is isosceles. So \(\angle{MON}=\angle{MNO}=\dfrac \pi 3\).
Since the sum of the angles in a triangle is \(\pi\), we have \(\angle{OMN}=\dfrac \pi 3\).
So the triangle \(OMN\) is equilateral.
The altitude \(MH\) bisects the base \(ON\).
Thus \(OH=\dfrac{1}{2}\).$$\begin{aligned} OH^2+HM^2 &=OM^2 \quad \text { (Pythagorean theorem for the right triangle } OHM)\\ \left(\frac{1}{2}\right)^2 + HM^2 &=1 \\ HM^2 &=\frac{3}{4} \\ HM &=\frac{\sqrt{3}}{2} \quad \text { since } HM\geqslant 0\end{aligned}$$As \(\cos \theta\) is the \(x\)-coordinate of \(M\) and \(\sin \theta\) is the \(y\)-coordinate of \(M\):$$\cos \frac{\pi}{3}=\frac{1}{2} \quad \text { and } \quad \sin \frac{\pi}{3}=\frac{\sqrt{3}}{2}$$
Proposition Multiples of \(\frac{\pi}{6}\)

The coordinates of each point are found by applying reflection symmetries over the axes or the origin.
Example
Find \(\cos \dfrac{2 \pi}{3}\) and \(\sin \dfrac{2 \pi}{3}\).
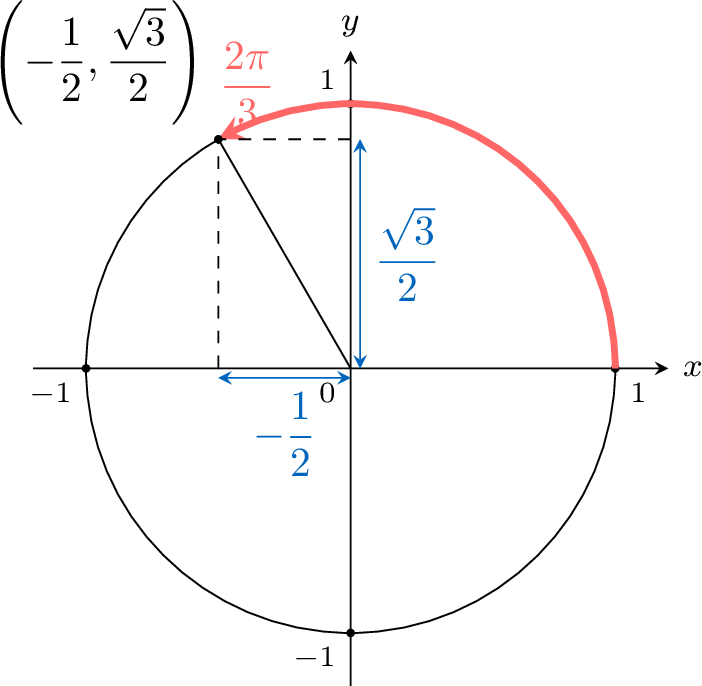
Tangent Function
Definition Tangent Function
The tangent of an angle \(\theta\) is defined, whenever \(\cos \theta \neq 0\), as the ratio of the sine to the cosine:$$\tan \theta = \frac{\sin \theta}{\cos \theta}.$$Equivalently, \(\tan \theta\) is defined for all real \(\theta\) such that \(\theta \neq \dfrac{\pi}{2} + k\pi\) for any integer \(k\).
Proposition Geometric Interpretation of Tangent
On the unit circle, for any angle \(\theta\) with \(\cos \theta \neq 0\), the ray from the origin forming an angle \(\theta\) with the positive \(x\)-axis meets the vertical tangent line \(x = 1\) at the point \((1,\tan \theta)\). In particular, \(\tan \theta\) is the \(y\)-coordinate of this intersection point.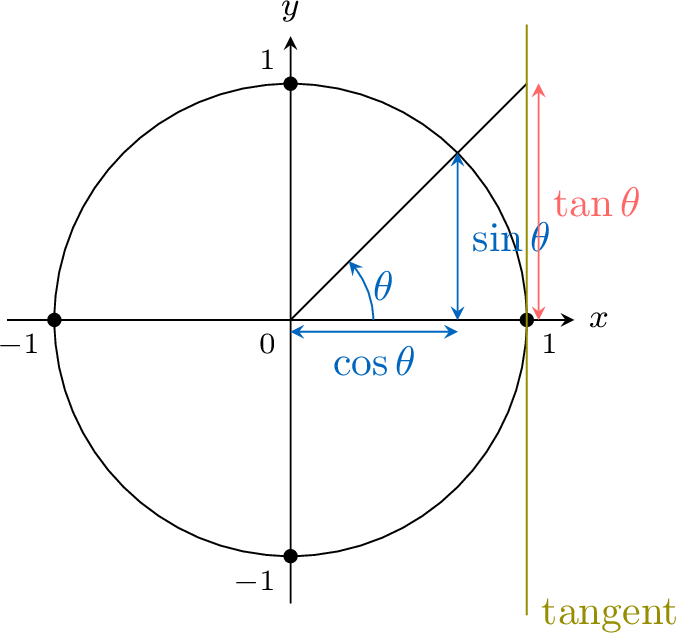
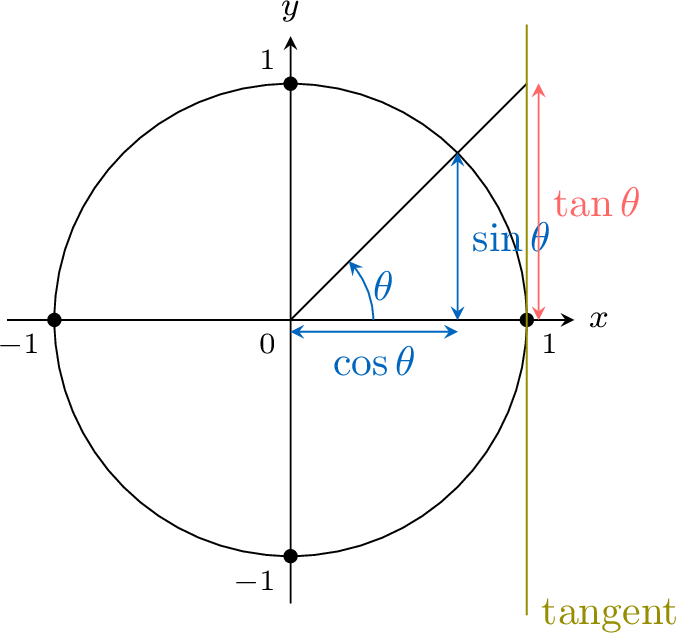
The ray from the origin at an angle \(\theta\) passes through the point \(P(\cos \theta, \sin \theta)\) on the unit circle.Provided \(\cos \theta \neq 0\), the slope of the line through the origin and \(P\) is$$\frac{\sin \theta}{\cos \theta} = \tan \theta,$$so the equation of this line is \(y = (\tan \theta)\,x\).The intersection of this line with the vertical line \(x = 1\) occurs when \(y = (\tan \theta)\cdot 1 = \tan \theta\). Thus, the intersection point is \((1,\tan \theta)\).
Proposition Tangent Values for Common Angles
| \(\theta\) | \(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) |
| \(0\) | \(0\) | \(1\) | \(0\) |
| \(\dfrac{\pi}{6}\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{\sqrt{3}}{3}\) |
| \(\dfrac{\pi}{4}\) | \(\dfrac{\sqrt{2}}{2}\) | \(\dfrac{\sqrt{2}}{2}\) | \(1\) |
| \(\dfrac{\pi}{3}\) | \(\dfrac{\sqrt{3}}{2}\) | \(\dfrac{1}{2}\) | \(\sqrt{3}\) |
| \(\dfrac{\pi}{2}\) | \(1\) | \(0\) | undefined |
Angle Sum and Difference Identities
Proposition Cosine of Difference
$$\cos (A - B) = \cos A \cos B + \sin A \sin B.$$
Consider two unit vectors on the unit circle:$$\vec{u} = \begin{pmatrix}\cos A \\
\sin A \end{pmatrix}\quad\text{and}\quad\vec{v} = \begin{pmatrix}\cos B \\
\sin B \end{pmatrix}.$$The angle between \(\vec{u}\) and \(\vec{v}\) is \(A - B\).
We can express the dot product \(\vec{u} \cdot \vec{v}\) in two ways: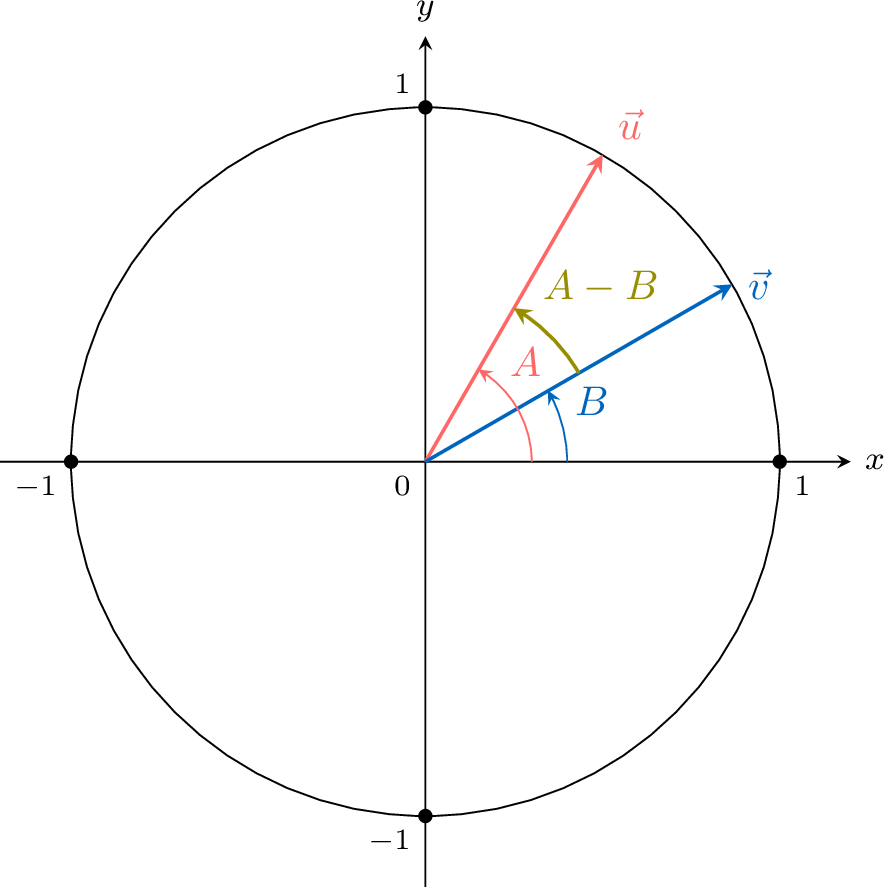
We can express the dot product \(\vec{u} \cdot \vec{v}\) in two ways:
- Using the geometric definition:$$\vec{u} \cdot \vec{v} = \|\vec{u}\| \,\|\vec{v}\| \cos(A - B) = 1 \cdot 1 \cdot \cos(A - B) = \cos(A - B).$$
- Using the component form:$$\vec{u} \cdot \vec{v}= \begin{pmatrix}\cos A \\ \sin A \end{pmatrix}\cdot \begin{pmatrix}\cos B \\ \sin B \end{pmatrix}= (\cos A)(\cos B) + (\sin A)(\sin B).$$

Proposition Cosine of Sum
$$\cos (A + B) = \cos A \cos B - \sin A \sin B.$$
Substitute \(B\) by \(-B\) in the cosine difference formula:$$\begin{aligned}\cos(A + B) &= \cos\bigl(A - (-B)\bigr)\\
&= \cos A \cos(-B) + \sin A \sin(-B)\\
&= \cos A \cos B + \sin A (-\sin B)\quad(\text{since } \cos(-\theta) = \cos \theta\text{ and }\sin(-\theta) = -\sin \theta)\\
&= \cos A \cos B - \sin A \sin B.\end{aligned}$$
Proposition Sine of Sum and Difference
$$\sin (A + B) = \sin A \cos B + \cos A \sin B,$$$$\sin (A - B) = \sin A \cos B - \cos A \sin B.$$
Using the complementary angle identity \(\sin \theta = \cos\left(\dfrac{\pi}{2} - \theta\right)\):$$\begin{aligned}\sin(A + B) &= \cos\left(\frac{\pi}{2} - (A + B)\right)\\
&= \cos\left( \left(\frac{\pi}{2} - A\right) - B \right)\\
&= \cos\left(\frac{\pi}{2} - A\right) \cos B + \sin\left(\frac{\pi}{2} - A\right) \sin B\\
&= \sin A \cos B + \cos A \sin B.\end{aligned}$$For the difference, write$$\begin{aligned}\sin(A - B) &= \sin\bigl(A + (-B)\bigr)\\
&= \sin A \cos(-B) + \cos A \sin(-B)\\
&= \sin A \cos B - \cos A \sin B.\end{aligned}$$
Proposition Tangent of Sum and Difference
For angles \(A\) and \(B\) such that all expressions below are defined,$$\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B},$$$$\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B}.$$
Assume \(\cos A \cos B \neq 0\) and \(\cos(A + B) \neq 0\) so that all ratios below are defined:$$\begin{aligned}\tan(A + B) &= \frac{\sin(A + B)}{\cos(A + B)} \\
&= \frac{\sin A \cos B + \cos A \sin B}{\cos A \cos B - \sin A \sin B} \\
&= \frac{\dfrac{\sin A \cos B + \cos A \sin B}{\cos A \cos B}}{\dfrac{\cos A \cos B - \sin A \sin B}{\cos A \cos B}} \quad \text{(divide numerator and denominator by } \cos A \cos B\text{)} \\
&= \frac{\dfrac{\sin A}{\cos A} + \dfrac{\sin B}{\cos B}}{1 - \dfrac{\sin A \sin B}{\cos A \cos B}}\\
&= \frac{\tan A + \tan B}{1 - \tan A \tan B}.\end{aligned}$$The formula for \(\tan(A-B)\) is obtained by replacing \(B\) with \(-B\) and using \(\tan(-B) = -\tan B\).