Time
Introduction
Time is a big part of our everyday lives! It helps us plan what we do, keep our schedules on track, and remember special moments. Learning about time lets us answer fun and useful questions like:
- What time does my favorite movie start?
- How long will it take to drive to the beach?
- When is the next school holiday?
- When did dinosaurs roam the Earth?
24-Hour Time Format
Definition 24-Hour Time Format
The 24-hour time format is a way to tell time without using AM or PM. It counts all 24 hours in a day, from 00:00 (midnight) to 23:59 (almost midnight again). It’s used by pilots, doctors, and people all over the world!

Example
Write 6:15 PM in 24-hour time.
Since 6:15 PM is 6 hours after noon (12:00):$$\begin{aligned}[t]6:15 \, \text{PM} &= 12 \, \text{h} + 6 \, \text{h} + 15 \, \text{min} \\&= 18 \, \text{h} + 15 \, \text{min} \\&= 18:15\end{aligned}$$So, 6:15 PM is 18:15 in 24-hour time.
Units of Time
A unit of time is a way to measure how long something takes. We use different units depending on what we’re timing!
Definition Common Units of Time
Here are the units we use most often:
- Seconds (s) – for quick things, like a race.
- Minutes (min) – for short activities, like a break.
- Hours (h) – for longer events, like school.
- Days (d) – for full days, like a weekend.
- Weeks (wk) – for several days, like a vacation.
- Months (mo) – for parts of a year, like summer.
- Years (yr) – for long periods, like your age.
- Centuries (c) – for very long times, like history.
Example
Which unit of time would you use to measure how long it takes to run 100 meters?
We use seconds because running 100 meters is a quick event.
So, the unit is seconds (s).
So, the unit is seconds (s).
Converting Units of Time
Definition Converting Units of Time
To change between units of time, use these facts: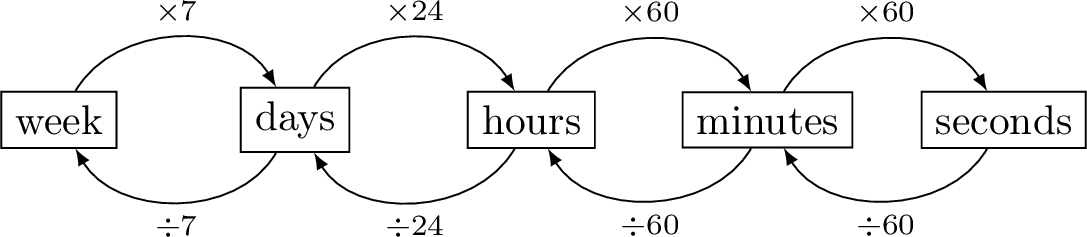
- 1 minute = 60 seconds
- 1 hour = 60 minutes
- 1 day = 24 hours
- 1 week = 7 days
- 1 year = 365 days
- 1 century = 100 years

Here’s how to convert:
- Use multiplication to go from a bigger unit to a smaller one (like minutes to seconds).
- Use division to go from a smaller unit to a bigger one (like minutes to hours).
Example
Convert 2 minutes to seconds.
Since 1 minute = 60 seconds:$$\begin{aligned}[t]2 \, \text{min} &= 2 \times 60 \, \text{s} \\&= 120 \, \text{s}\end{aligned}$$So, 2 minutes is 120 seconds.
Example
Convert 120 minutes to hours.
Since 1 hour = 60 minutes:$$\begin{aligned}[t]120 \, \text{min} &= 120 \div 60 \, \text{h} \\&= 2 \, \text{h}\end{aligned}$$So, 120 minutes is 2 hours.
Method Converting Seconds to Minutes and Seconds
To change seconds into minutes and seconds, divide by 60 (since 1 minute = 60 seconds). The answer tells you how many minutes, and what’s left over is the extra seconds.
Example
Write 140 seconds as minutes and seconds.
Divide 140 by 60: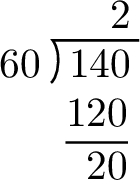
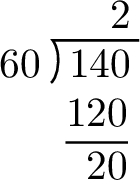
Adding and Subtracting Time
Method Adding and Subtracting Time
When you add or subtract time, make sure the units match (like all in minutes or all in hours). Convert if needed, then do the math!
Example
Add 2 hours 30 minutes and 1 hour 45 minutes.
Add hours and minutes separately:$$\begin{aligned}[t]2 \, \text{h} \, 30 \, \text{min} + 1 \, \text{h} \, 45 \, \text{min} &= (2 \, \text{h} + 1 \, \text{h}) + (30 \, \text{min} + 45 \, \text{min}) \\&= 3 \, \text{h} + 75 \, \text{min} \\&= 3 \, \text{h} + (60 \, \text{min} + 15 \, \text{min}) \\&= 3 \, \text{h} + 1 \, \text{h} + 15 \, \text{min} \\&= 4 \, \text{h} \, 15 \, \text{min}\end{aligned}$$So, the total is 4 hours and 15 minutes.
Example
Subtract 3 hours 15 minutes from 5 hours 30 minutes.
Subtract hours and minutes separately:$$\begin{aligned}[t]5 \, \text{h} \, 30 \, \text{min} - 3 \, \text{h} \, 15 \, \text{min} &= (5 \, \text{h} - 3 \, \text{h}) + (30 \, \text{min} - 15 \, \text{min}) \\&= 2 \, \text{h} + 15 \, \text{min} \\&= 2 \, \text{h} \, 15 \, \text{min}\end{aligned}$$So, the difference is 2 hours and 15 minutes.
Time Problems
Method Solving Time Problems
To solve time problems, you might need to add, subtract, or think step-by-step. Use what you know about units and conversions!
Example
A bus trip takes 2 hours and 15 minutes. If it leaves at 12:30, what time will it arrive?
Add the trip time to the start time:$$\begin{aligned}[t]12:30 + 2 \, \text{h} \, 15 \, \text{min} &= (12 \, \text{h} + 2 \, \text{h}) + (30 \, \text{min} + 15 \, \text{min}) \\&= 14 \, \text{h} + 45 \, \text{min} \\&= 14:45\end{aligned}$$So, the bus arrives at 14:45.
Timelines
Definition Timeline
A timeline is a picture that shows events in order, like a line of history!
Timelines help us see when things happened and how long they lasted. They’re great for history, projects, or even planning your day!
Example
This timeline shows two famous kings of France in the 1600s:

Louis XIII started being king in 1610.
Definition AD and BC
- BC means “Before Christ” (before Jesus was born).
- AD means “Anno Domini” (after Jesus was born).
Example
This timeline shows two big events in ancient Rome:

Julius Caesar was born in 100 BC.