\( \definecolor{colordef}{RGB}{249,49,84} \definecolor{colorprop}{RGB}{18,102,241} \)

Subtraction Within 20

Definitions

Subtracting Numbers Within 10

Exercise
\(9-1=\)

  • \(-\) \(=\)
  • \(9-1=8\)

Exercise
\(10-2=\)

  • \(-\) \(=\)
  • \(10-2=8\)

Exercise
\(7-3=\)

  • \(-\) \(=\)
  • \(7-3=4\)

Exercise
\(9-5=\)

  • \(-\) \(=\)
  • \(9-5=4\)

Exercise
\(6-2=\)

  • \(-\) \(=\)
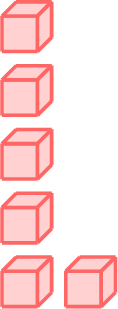  • \(6-2=4\)

Exercise
\(8-3=\)

  • \(-\) \(=\)
  • \(8-3=5\)

Exercise
\(10-6=\)

  • \(-\) \(=\)
  • \(10-6=4\)

Subtracting by Taking Away Units

Exercise
\(14-1=\)
\(-\) \(=\)

  • \(-\) \(=\)
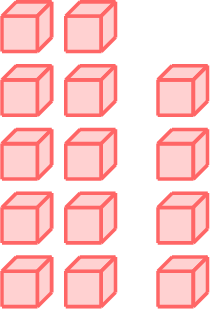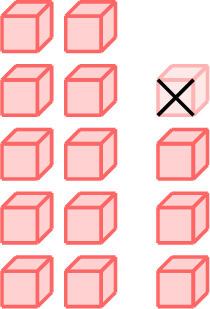
  • \(14-1=13\)

Exercise
\(15-2=\)
\(-\) \(=\)

  • \(-\) \(=\)
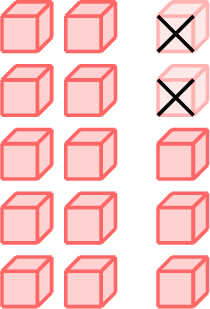
  • \(15-2=13\)

Exercise
\(16-1=\)
\(-\) \(=\)

  • \(-\) \(=\)
  • \(16-1=15\)

Exercise
\(16-3=\)
\(-\) \(=\)

  • \(-\) \(=\)
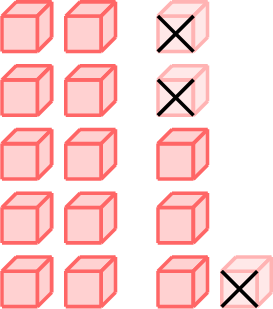
  • \(16-3=13\)

Exercise
\(14-4=\)
\(-\) \(=\)

  • \(-\) \(=\)
  • \(14-4=10\)

Exercise
\(17-5=\)
\(-\) \(=\)

  • \(-\) \(=\)
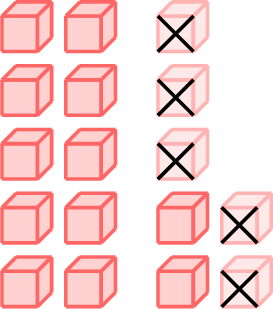
  • \(17-5=12\)

Subtracting by Taking Away Units and One Ten

Exercise
\(13-10=\)
\(-\) \(=\)

  • \(-\) \(=\)
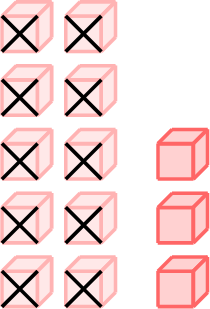
  • \(13-10=3\)

Exercise
\(14-11=\)
\(-\) \(=\)

  • \(-\) \(=\)
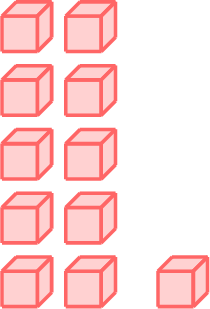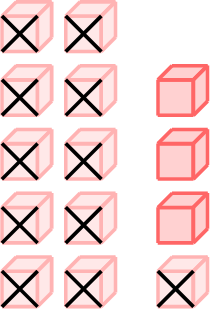
  • \(14-11=3\)

Exercise
\(13-12=\)
\(-\) \(=\)

  • \(-\) \(=\)
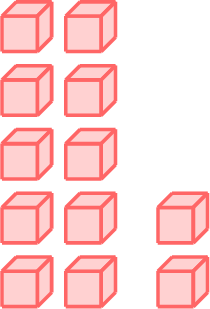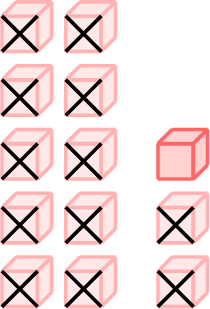
  • \(13-12=1\)

Exercise
\(15-13=\)
\(-\) \(=\)

  • \(-\) \(=\)
  • \(15-13=2\)

Exercise
\(13-10=\)
\(-\) \(=\)

  • \(-\) \(=\)
  • \(13-10=3\)

Exercise
\(15-14=\)
\(-\) \(=\)

  • \(-\) \(=\)
  • \(15-14=1\)

Exercise
\(18-16=\)
\(-\) \(=\)

  • \(-\) \(=\)
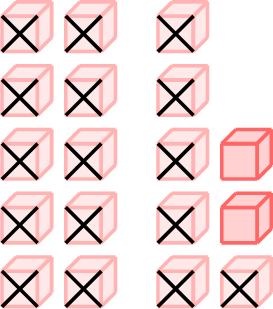
  • \(18-16=2\)

Subtracting Multiple Numbers

Exercise
\(5 - 1 - 1 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]5 - 1 - 1 &= 4 - 1\\&= 3\\\end{aligned}\)

Exercise
\(5-2-1=\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]5-2-1&=3-1\\&=2\\\end{aligned}\)

Exercise
\(6 - 3 - 2 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]6 - 3 - 2 &= 3 - 2\\&= 1\\\end{aligned}\)

Exercise
\(7 - 1 - 3 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]7 - 1 - 3 &= 6 - 3\\&= 3\\\end{aligned}\)

Exercise
\(8 - 2 - 4 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]8 - 2 - 4 &= 6 - 4\\&= 2\\\end{aligned}\)

Exercise
\(6 - 4 - 1 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    7 \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]6 - 4 - 1 &= 2 - 1\\&= 1\\\end{aligned}\)

Exercise
\(9 - 4 - 3 =\)
\(-\) \(-\) \(=\)

  • \(-\) \(-\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]9 - 4 - 3 &= 5 - 3\\&= 2\\\end{aligned}\)

Breaking Down Numbers

Exercise
\(3=\textcolor{colordef}{2}+\)

  • \(=\) \(+\)
  • \(3=\textcolor{colordef}{2}+\textcolor{colorprop}{1}\)

Exercise
\(5 = \textcolor{colordef}{3} +\)

  • \(=\) \(+\)
  • \(5 = \textcolor{colordef}{3} + \textcolor{colorprop}{2}\)

Exercise
\(4 = \textcolor{colordef}{1} +\)

  • \(=\) \(+\)
  • \(4 = \textcolor{colordef}{1} + \textcolor{colorprop}{3}\)

Exercise
\(7 = \textcolor{colordef}{4} +\)

  • \(=\) \(+\)
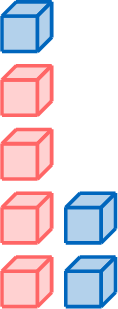  • \(7 = \textcolor{colordef}{4} + \textcolor{colorprop}{3}\)

Exercise
\(8 = \textcolor{colordef}{3} +\)

  • \(=\) \(+\)
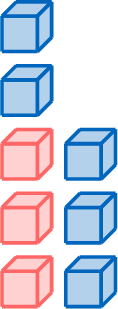  • \(8 = \textcolor{colordef}{3} + \textcolor{colorprop}{5}\)

Exercise
\(9 = \textcolor{colordef}{7} +\)

  • \(=\) \(+\)
  • \(9 = \textcolor{colordef}{7} + \textcolor{colorprop}{2}\)

Exercise
\(10 = \textcolor{colordef}{6} +\)

  • \(=\) \(+\)
  • \(10 = \textcolor{colordef}{6} + \textcolor{colorprop}{4}\)

Number Line Method

Subtracting Using the Number Line

Exercise
\(13-4=\)

  • \(13-4=9\)

Exercise
\(12-6=\)

  • \(12-6=6\)

Exercise
\(14-5=\)

  • \(14-5=9\)

Exercise
\(15-6=\)

  • \(15-6=9\)

Exercise
\(11-6=\)

  • \(11-6=5\)

Exercise
\(17-6=\)

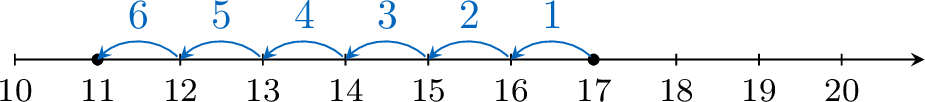
  • \(11-6=5\)

Making 10 Method

Breaking Down Numbers to Make Ten

Exercise
\(11-3=11-1-\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(11-3=11-1-2\)

Exercise
\(12 - 3 = 12 - 2 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(12 - 3 = 12 - 2 - 1\)

Exercise
\(14 - 6 = 14 - 4 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(14 - 6 = 14 - 4 - 2\)

Exercise
\(12 - 7 = 12 - 2 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(11 - 9 = 11 - 1 - 8\)

Exercise
\(11 - 9 = 11 - 1 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(11 - 9 = 11 - 1 - 8\)

Exercise
\(13 - 7 = 13 - 3 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(13 - 7 = 13 - 3 - 4\)

Exercise
\(15 - 9 = 15 - 5 -\)

  • \(-\) \(=\) \(-\) \(-\)

  • \(15 - 9 = 15 - 5 - 4\)

Subtracting from Ten

Exercise
\(10-3=\)

  • \(-\) \(=\)
  • \(10 - 3=7\)

Exercise
\(10-2=\)

  • \(-\) \(=\)
  • \(10 - 2=8\)

Exercise
\(10-4=\)

  • \(-\) \(=\)
  • \(10 - 4=6\)

Exercise
\(10-1=\)

  • \(-\) \(=\)
  • \(10 - 1=9\)

Exercise
\(10-5=\)

  • \(-\) \(=\)
  • \(10 - 5=5\)

Exercise
\(10-7=\)

  • \(-\) \(=\)
  • \(10 - 7=3\)

Exercise
\(10-6=\)

  • \(-\) \(=\)
  • \(10 - 6=4\)

Making 10 after Breaking Down Numbers

Exercise
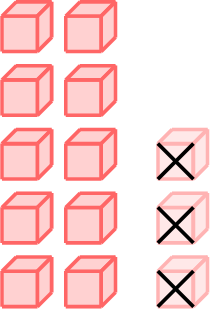
\(13-5\) \(=\) \(13-3-2\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]13 - 5&=13 - 3 - 2\\&=10 - 2\\&=8\\\end{aligned}\)

Exercise
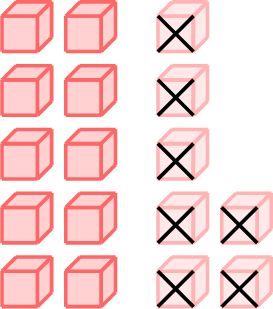
\(17-8\) \(=\) \(17-7-1\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
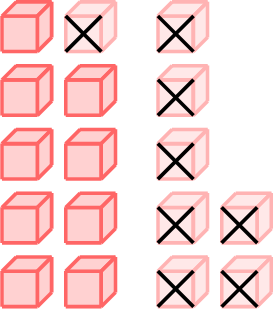
  • \(\begin{aligned}[t]17 - 8 &= 17 - 7 - 1\\&=10 - 1\\&=9\\\end{aligned}\)

Exercise
\(16-8\) \(=\) \(16-6-2\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

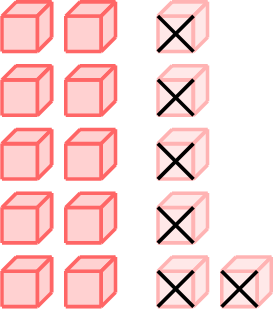    \(\textcolor{white}{-}\) \(=\)
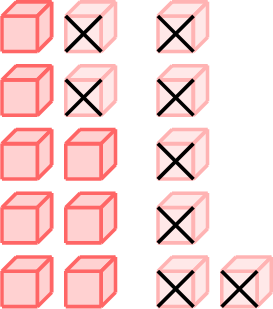
  • \(\begin{aligned}[t]16 - 8 &= 16 - 6 - 2\\&=10 - 2\\&=8\\\end{aligned}\)

Exercise
\(15-8\) \(=\) \(15-5-3\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

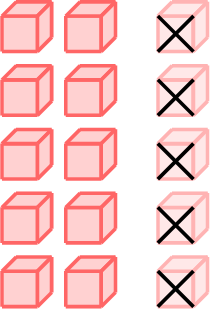    \(\textcolor{white}{-}\) \(=\)
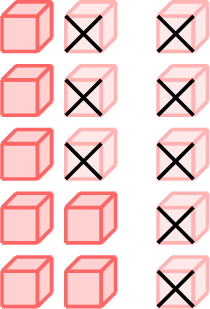
  • \(\begin{aligned}[t]15 - 8 &= 15 - 5 - 3\\&=10 - 3\\&=7\\\end{aligned}\)

Exercise
\(14-7\) \(=\) \(14-4-3\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
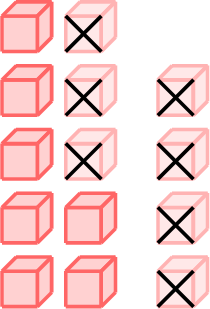
  • \(\begin{aligned}[t]14 - 7 &= 14 - 4 - 3\\&=10 - 3\\&=7\\\end{aligned}\)

Exercise
\(18-9\) \(=\) \(18-8-1\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
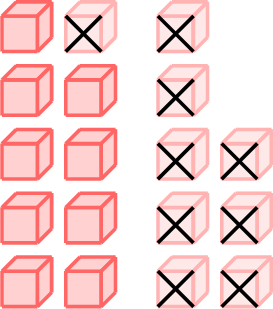
  • \(\begin{aligned}[t]18 - 9 &= 18 - 8 - 1\\&=10 - 1\\&=9\\\end{aligned}\)

Exercise
\(13-7\) \(=\) \(13-3-4\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
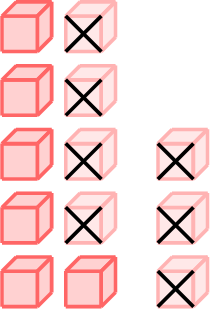
  • \(\begin{aligned}[t]13 - 7 &= 13 - 3 - 4\\&=10 - 4\\&=6\\\end{aligned}\)

Exercise
\(13-9\) \(=\) \(13-3-6\)
\(=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
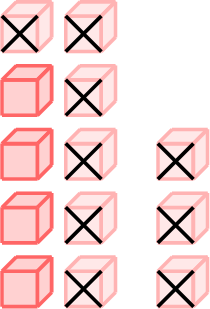
  • \(\begin{aligned}[t]13 - 9 &= 13 - 3 - 6\\&=10 - 6\\&=4\\\end{aligned}\)

Subtracting Number Within 20

Exercise
\(13-5=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]13 - 5&=13 - 3 - 2\\&=10 - 2\\&=8\\\end{aligned}\)

Exercise
\(17-8=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]17 - 8 &= 17 - 7 - 1\\&=10 - 1\\&=9\\\end{aligned}\)

Exercise
\(16-8=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]16 - 8 &= 16 - 6 - 2\\&=10 - 2\\&=8\\\end{aligned}\)

Exercise
\(15-8=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]15 - 8 &= 15 - 5 - 3\\&=10 - 3\\&=7\\\end{aligned}\)

Exercise
\(14-7=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]14 - 7 &= 14 - 4 - 3\\&=10 - 3\\&=7\\\end{aligned}\)

Exercise
\(18-9=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]18 - 9 &= 18 - 8 - 1\\&=10 - 1\\&=9\\\end{aligned}\)

Exercise
\(13-7=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]13 - 7 &= 13 - 3 - 4\\&=10 - 4\\&=6\\\end{aligned}\)

Exercise
\(13-9=\)

  • \(-\) \(=\) \(-\) \(-\)

    \(\textcolor{white}{-}\) \(=\) \(-\)

    \(\textcolor{white}{-}\) \(=\)
  • \(\begin{aligned}[t]13 - 9 &= 13 - 3 - 6\\&=10 - 6\\&=4\\\end{aligned}\)

Addition and Subtraction Link

Finding Subtraction Using Addition

Exercise
If we know that \(\textcolor{colordef}{17}+\textcolor{colorprop}{14}=\textcolor{olive}{31}\), then \(\textcolor{olive}{31}-\textcolor{colordef}{17}=\) .

  • We add to find the total:$$\begin{aligned}\textcolor{colordef}{\text{part 1}} + \textcolor{colorprop}{\text{part 2}}&=\textcolor{olive}{\text{total}}\\ \textcolor{colordef}{17}+\textcolor{colorprop}{14} &= \textcolor{olive}{31}\end{aligned}$$
  • We subtract to find a part:$$\begin{aligned} \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part 1}}&=\textcolor{colorprop}{\text{part 2}}\\ \textcolor{olive}{31} - \textcolor{colordef}{17} &= \textcolor{colorprop}{14}\end{aligned}$$

Exercise
If we know that \(\textcolor{colordef}{50}+\textcolor{colorprop}{45}=\textcolor{olive}{95}\), then \(\textcolor{olive}{95}-\textcolor{colordef}{50}=\) .

  • We add to find the total:$$\begin{aligned}\textcolor{colordef}{\text{part 1}} + \textcolor{colorprop}{\text{part 2}}&=\textcolor{olive}{\text{total}}\\ \textcolor{colordef}{50}+\textcolor{colorprop}{45} &= \textcolor{olive}{95}\end{aligned}$$
  • We subtract to find a part:$$\begin{aligned} \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part 1}}&=\textcolor{colorprop}{\text{part 2}}\\ \textcolor{olive}{95} - \textcolor{colordef}{50} &= \textcolor{colorprop}{45}\end{aligned}$$

Exercise
If we know that \(\textcolor{colordef}{18}+\textcolor{colorprop}{82}=\textcolor{olive}{100}\), then \(\textcolor{olive}{100}-\textcolor{colordef}{18}=\) .

  • We add to find the total:$$\begin{aligned}\textcolor{colordef}{\text{part 1}} + \textcolor{colorprop}{\text{part 2}}&=\textcolor{olive}{\text{total}}\\ \textcolor{colordef}{18}+\textcolor{colorprop}{82} &= \textcolor{olive}{100}\end{aligned}$$
  • We subtract to find a part:$$\begin{aligned} \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part 1}}&=\textcolor{colorprop}{\text{part 2}}\\ \textcolor{olive}{100} - \textcolor{colordef}{18} &= \textcolor{colorprop}{82}\end{aligned}$$

Exercise
If we know that \(\textcolor{colordef}{78}+\textcolor{colorprop}{2}=\textcolor{olive}{80}\), then \(\textcolor{olive}{80}-\textcolor{colordef}{78}=\) .

  • We add to find the total:$$\begin{aligned}\textcolor{colordef}{\text{part 1}} + \textcolor{colorprop}{\text{part 2}}&=\textcolor{olive}{\text{total}}\\ \textcolor{colordef}{78}+\textcolor{colorprop}{2} &= \textcolor{olive}{80}\end{aligned}$$
  • We subtract to find a part:$$\begin{aligned} \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part 1}}&=\textcolor{colorprop}{\text{part 2}}\\ \textcolor{olive}{80} - \textcolor{colordef}{78} &= \textcolor{colorprop}{2}\end{aligned}$$

Finding the Missing Subtrahend

Exercise
\(\textcolor{olive}{4}-\) \(=\textcolor{colordef}{1}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}- \textcolor{colorprop}{\text{part}}&=\textcolor{colordef}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{4}- \textcolor{colordef}{1}&=\textcolor{colorprop}{3}\\\textcolor{olive}{4}- \textcolor{colorprop}{3}&=\textcolor{colordef}{1}\end{aligned}\)

Exercise
\(\textcolor{olive}{5}-\) \(=\textcolor{colordef}{2}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}- \textcolor{colorprop}{\text{part}}&=\textcolor{colordef}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{5}- \textcolor{colordef}{2}&=\textcolor{colorprop}{3}\\\textcolor{olive}{5}- \textcolor{colorprop}{3}&=\textcolor{colordef}{2}\end{aligned}\)

Exercise
\(\textcolor{olive}{7}-\) \(=\textcolor{colordef}{5}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}- \textcolor{colorprop}{\text{part}}&=\textcolor{colordef}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{7}- \textcolor{colordef}{5}&=\textcolor{colorprop}{2}\\\textcolor{olive}{7}- \textcolor{colorprop}{2}&=\textcolor{colordef}{5}\end{aligned}\)

Exercise
\(\textcolor{olive}{6}-\) \(=\textcolor{colordef}{4}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}- \textcolor{colorprop}{\text{part}}&=\textcolor{colordef}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{6}- \textcolor{colordef}{2}&=\textcolor{colorprop}{4}\\\textcolor{olive}{6}- \textcolor{colorprop}{4}&=\textcolor{colordef}{2}\end{aligned}\)

Exercise
\(\textcolor{olive}{8}-\) \(=\textcolor{colordef}{3}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}- \textcolor{colorprop}{\text{part}}&=\textcolor{colordef}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{8}- \textcolor{colordef}{3}&=\textcolor{colorprop}{5}\\\textcolor{olive}{8}- \textcolor{colorprop}{5}&=\textcolor{colordef}{3}\end{aligned}\)

Finding the Total in Subtraction Problems

Exercise
\(-\textcolor{colordef}{2}=\textcolor{colorprop}{3}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}&=\textcolor{colordef}{\text{part}}+\textcolor{colorprop}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{5}&= \textcolor{colordef}{2}+\textcolor{colorprop}{3}\\\textcolor{olive}{5}- \textcolor{colordef}{2}&=\textcolor{colorprop}{3}\end{aligned}\)

Exercise
\(-\textcolor{colordef}{4}=\textcolor{colorprop}{2}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}&=\textcolor{colordef}{\text{part}}+\textcolor{colorprop}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{6}&= \textcolor{colordef}{4}+\textcolor{colorprop}{2}\\\textcolor{olive}{6}- \textcolor{colordef}{4}&=\textcolor{colorprop}{2}\end{aligned}\)

Exercise
\(-\textcolor{colordef}{3}=\textcolor{colorprop}{4}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}&=\textcolor{colordef}{\text{part}}+\textcolor{colorprop}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{7}&= \textcolor{colordef}{3}+\textcolor{colorprop}{4}\\\textcolor{olive}{7}- \textcolor{colordef}{3}&=\textcolor{colorprop}{4}\end{aligned}\)

Exercise
\(-\textcolor{colordef}{5}=\textcolor{colorprop}{3}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}&=\textcolor{colordef}{\text{part}}+\textcolor{colorprop}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{8}&= \textcolor{colordef}{5}+\textcolor{colorprop}{3}\\\textcolor{olive}{8}- \textcolor{colordef}{5}&=\textcolor{colorprop}{3}\end{aligned}\)

Exercise
\(-\textcolor{colordef}{6}=\textcolor{colorprop}{3}\)

  • \(\begin{aligned}[t] \textcolor{olive}{\text{total}}- \textcolor{colordef}{\text{part}}&=\textcolor{colorprop}{\text{part}}\\\textcolor{olive}{\text{total}}&=\textcolor{colordef}{\text{part}}+\textcolor{colorprop}{\text{part}}\end{aligned}\)
  • \(\begin{aligned}[t]\textcolor{olive}{9}&= \textcolor{colordef}{6}+\textcolor{colorprop}{3}\\\textcolor{olive}{9}- \textcolor{colordef}{6}&=\textcolor{colorprop}{3}\end{aligned}\)

Finding the Missing Addend

Exercise
\(\textcolor{colordef}{9}+ \) \(= \textcolor{olive}{11}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{9}+\textcolor{colorprop}{2}=\textcolor{olive}{11}\)

Exercise
\(\textcolor{colordef}{7}+ \) \(= \textcolor{olive}{12}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{7}+\textcolor{colorprop}{5}=\textcolor{olive}{12}\)

Exercise
\(\textcolor{colordef}{6}+ \) \(= \textcolor{olive}{12}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{6}+\textcolor{colorprop}{6}=\textcolor{olive}{12}\)

Exercise
\(\textcolor{colordef}{11}+ \) \(= \textcolor{olive}{14}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{11}+\textcolor{colorprop}{3}=\textcolor{olive}{14}\)

Exercise
\(\textcolor{colordef}{8}+ \) \(= \textcolor{olive}{12}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{8}+\textcolor{colorprop}{4}=\textcolor{olive}{12}\)

Exercise
\(\textcolor{colordef}{5}+ \) \(= \textcolor{olive}{12}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{5}+\textcolor{colorprop}{7}=\textcolor{olive}{12}\)

Exercise
\(\textcolor{colordef}{12}+ \) \(= \textcolor{olive}{15}\)

  • \(+\)\(=\)
  • \(\textcolor{colordef}{12}+\textcolor{colorprop}{3}=\textcolor{olive}{15}\)

Subtracting by Thinking Addition

Exercise
\(\textcolor{olive}{17}-\textcolor{colordef}{15}=\)

  • \(\textcolor{colordef}{15}+\textcolor{colorprop}{2}=\textcolor{olive}{17}\)
  • \(\textcolor{olive}{17}-\textcolor{colordef}{15}=\textcolor{colorprop}{2}\)

Exercise
\(\textcolor{olive}{11}-\textcolor{colordef}{9}=\)

  • \(\textcolor{colordef}{9}+\textcolor{colorprop}{2}=\textcolor{olive}{11}\)
  • \(\textcolor{olive}{11}-\textcolor{colordef}{9}=\textcolor{colorprop}{2}\)

Exercise
\(\textcolor{olive}{19}-\textcolor{colordef}{15}=\)

  • \(\textcolor{colordef}{15}+\textcolor{colorprop}{4}=\textcolor{olive}{19}\)
  • \(\textcolor{olive}{19}-\textcolor{colordef}{15}=\textcolor{colorprop}{4}\)

Exercise
\(\textcolor{olive}{12}-\textcolor{colordef}{8}=\)

  • \(\textcolor{colordef}{8}+\textcolor{colorprop}{4}=\textcolor{olive}{12}\)
  • \(\textcolor{olive}{12}-\textcolor{colordef}{8}=\textcolor{colorprop}{4}\)

Exercise
\(\textcolor{olive}{13}-\textcolor{colordef}{11}=\)

  • \(\textcolor{colordef}{11}+\textcolor{colorprop}{2}=\textcolor{olive}{13}\)
  • \(\textcolor{olive}{13}-\textcolor{colordef}{11}=\textcolor{colorprop}{2}\)

Exercise
\(\textcolor{olive}{14}-\textcolor{colordef}{9}=\)

  • \(\textcolor{colordef}{9}+\textcolor{colorprop}{5}=\textcolor{olive}{14}\)
  • \(\textcolor{olive}{14}-\textcolor{colordef}{9}=\textcolor{colorprop}{5}\)

Exercise
\(\textcolor{olive}{16}-\textcolor{colordef}{11}=\)

  • \(\textcolor{colordef}{11}+\textcolor{colorprop}{5}=\textcolor{olive}{16}\)
  • \(\textcolor{olive}{16}-\textcolor{colordef}{11}=\textcolor{colorprop}{5}\)

Problem-Solving Methods

Solving Real-World Problems

Exercise
Hugo and Louis are looking for shells. Hugo found 6 shells, and Louis found 9 shells.
How many shells do they have together in total?
shells

  • To find the total number of shells, start with the number of shells Hugo found, then add the number of shells Louis found.
  • So, the total number of shells is \(\textcolor{colordef}{6} + \textcolor{colorprop}{9}=\textcolor{olive}{15}\).
  • \(+\)\(=\)

Exercise
Last month, Louis weighed 14 kilos. This month, he gained 5 kilos. How much does Louis weigh now?
kilos

  • To find Louis's current weight, start with last month's weight, and then add the weight gained this month.
  • So, Louis’s weight is now \(\textcolor{colordef}{14} + \textcolor{colorprop}{5}=\textcolor{olive}{19}\) kilos.
  • \(+\)\(=\)

Exercise
A bookshelf has 11 books. You take 3 books to read.
How many books are left on the bookshelf?
books

  • Start with the total of 11 books and subtract the 3 books that you took.
  • The books left are \(\textcolor{olive}{11} - \textcolor{colordef}{3}=\textcolor{colorprop}{8}\)
  • \(-\)\(=\)

Exercise
Su has saved 12 dollars from her allowance. Li has saved 5 dollars more than Su.
How much money has Li saved?
dollars

  • To find the amount Li has saved, start with the amount Su saved, and add the extra amount Li saved.
  • So, the total savings for Li is \(\textcolor{colordef}{12} + \textcolor{colorprop}{5}=\textcolor{olive}{17}\) dollars.
  • \(+\)\(=\)

Exercise
You have 17 marbles. You give 4 marbles to a friend.
How many marbles do you have left?
marbles

  • Start with the total of 17 marbles and subtract the 4 marbles that you gave away.
  • The marbles left are \(\textcolor{olive}{17} - \textcolor{colordef}{4}=\textcolor{colorprop}{13}\)
  • \(-\)\(=\)

Exercise
During the holiday, Anjelaï read 5 more books than the 7 books she had planned to read.
How many books did she read in total?
books

  • To find the total number of books Anjelaï read, start with the 7 books she planned to read and add the 5 extra books she read.
  • So, the total number of books she read is \(\textcolor{colordef}{7} + \textcolor{colorprop}{5}=\textcolor{olive}{12}\) books.
  • \(+\)\(=\)

Exercise
You buy something for 6 dollars. You give the seller a 10 dollar bill.
How much change will you get back?
dollars

  • Start with the total amount given, which is 10 dollars, and subtract the cost of 6 dollars.
  • The change you get back is \(\textcolor{olive}{10} - \textcolor{colordef}{6} = \textcolor{colorprop}{4}\) dollars.
  • \(-\)\(=\)

Exercise
You start with 20 candies. You give 6 candies to a friend.
How many candies do you have left?
candies

  • Start with a total of 20 candies and subtract the 6 candies you gave away.
  • The candies left are \(\textcolor{olive}{20} - \textcolor{colordef}{6}=\textcolor{colorprop}{14}\)
  • \(-\)\(=\)

Exercise
Li won 8 marbles during recess. Tonight, he has 15 marbles.
How many marbles did he have this morning?
marbles

  • Start with the total number of marbles Li has now, which is 15 marbles, and subtract the 8 marbles he won.
  • The marbles he had this morning are \(\textcolor{olive}{15} - \textcolor{colordef}{8} = \textcolor{colorprop}{7}\).
  • \(-\)\(=\)

Exercise
Emma found 5 seashells at the beach in the afternoon. Now she has 12 seashells.
How many seashells did she already have before going to the beach?
seashells

  • Start with the total number of seashells Emma has now, which is 12, and subtract the 5 seashells she found.
  • The seashells she had before are \(\textcolor{olive}{12} - \textcolor{colordef}{5} = \textcolor{colorprop}{7}\).
  • \(-\)\(=\)