Set Theory
Definitions
Set
Definition Set
A set is a collection of objects, called elements.
We list its elements between curly brackets.
We list its elements between curly brackets.
Example
List all possible results when rolling a standard die 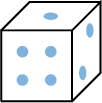 .
.
\(E=\{1,2,3,4,5,6\}=\{\) ,
,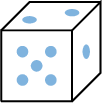 ,
,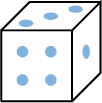 ,
,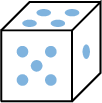 ,
,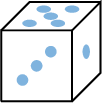 ,
,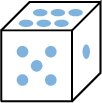 \(\}\).
\(\}\).
Definition Element
- An element is an object contained in a set.
- \(\in\) means "is an element of" or "belongs to".
- \(\notin\) means "is not an element of" or "does not belong to".
Example
\(2\in \{1,2,3,4,5,6\}\) and \(7\notin \{1,2,3,4,5,6\}\).
Definition Equal sets
Two sets are equal if they have exactly the same elements.
Example
Determine if the sets \(\{2,6,4\}\) and \(\{2,4,6\}\) are equal.
Yes, the sets \(\{2,6,4\}\) and \(\{2,4,6\}\) are equal because they contain the same elements: \(2\), \(4\), and \(6\).
Example
Determine if the sets \(\{1,2,3\}\) and \(\{1,2,4\}\) are equal.
No, the sets \(\{1,2,3\}\) and \(\{1,2,4\}\) are not equal because element \(3\) belongs to \(\{1,2,3\}\) but not to \(\{1,2,4\}\).
Definition Empty Set
The empty set is a set with no elements. It is written as \(\{\}\) or \(\emptyset\).
Natural Numbers
Definition Natural Numbers
The set of natural numbers, denoted \(\N\), is the set of counting numbers starting from zero:$$\N = \{0, 1, 2, 3, 4, 5, 6, \dots\}$$
Subsets
Definition Subset
A set \(A\) is a subset of a set \(B\) if every element in \(A\) is also in \(B\). We write this as \(A \subseteq B\).
Example
Is \(A \subseteq B\) when \(A = \{2, 4, 6\}\) and \(B = \{1, 2, 3, 4, 5, 6\}\)?
Check each element: 2, 4, and 6 from \(A\) are all in \(B = \{1, 2, 3, 4, 5, 6\}\). Since every element of \(A\) is in \(B\), \(A \subseteq B\).
Set-Builder Notation
Definition Set-Builder Notation
The set-builder notation is a way to describe a set by giving a rule that its elements must follow. It is written like this:$$\{x \in E \mid \text{condition on } x\}$$In this notation, \(x\) represents an element from a set \(E\), and the symbol \(\mid\) (or sometimes \(:\)) separates \(x\) from the condition it must meet. It reads: “the set of all \(x\) in \(E\) such that \(x\) follows the given condition.”
Example
Let \(E\) be the set of results from rolling a standard six-sided die  .
.
What are the elements of the set \(\{x \in E \mid x \text{ is even}\}\)?
What are the elements of the set \(\{x \in E \mid x \text{ is even}\}\)?
The set \(\{x \in E \mid x \text{ is even}\}\) contains all the even numbers in \(E\). Given \(E = \{1, 2, 3, 4, 5, 6\}\), the even numbers are 2, 4, and 6, so:$$\{x \in E \mid x \text{ is even}\} = \{2, 4, 6\}$$
Ordered Pair and n-Tuple
Definition Ordered Pair and n-Tuple
An ordered pair, denoted \((a, b)\) or sometimes \(ab\), is a pair of elements where the order matters.
More generally, an ordered n-tuple, denoted \((a_1, a_2, \dots, a_n)\), is a sequence of \(n\) elements where the order of the elements is significant. An ordered pair is a special case when \(n = 2\).
More generally, an ordered n-tuple, denoted \((a_1, a_2, \dots, a_n)\), is a sequence of \(n\) elements where the order of the elements is significant. An ordered pair is a special case when \(n = 2\).
Example
In a sprint relay race, two runners are paired up. Let \(L\) be Louis and \(H\) be Hugo. The ordered pair \((L, H)\) means Louis runs first, then passes the baton to Hugo. The ordered pair \((H, L)\) means Hugo runs first, then passes to Louis. These are different races.
Cardinality
Definition Cardinality
\(\Card{A}\) denotes the number of elements in the set \(A\).
Example
\(\Card{\{1,2,3,4,5,6\}}=6=\) 

Definition Finite and Infinite Sets
- A finite set has a finite number of elements. Informally, a finite set is a set which one could in principle count and finish counting.
- An infinite set is not a finite set.
Example
- \(\{1, 2, 3\}\) is finite because it has exactly 3 elements
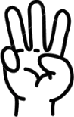 .
. - \(\N=\{0,1, 2, 3, \dots\}\) is infinite because the counting goes on forever without stopping.
Operations
Complement
Definition Universal set
A universal set is the set of all elements considered.
Definition Complement
The complement of a set \(A\), denoted \(A'\), consists of all elements in \(U\) that are not in \(A\). Sets \(A\) and \(A'\) are said to be complementary.
Example
Given the universe \(U = \{1, 2, 3, 4, 5, 6\}\) and the set \(A = \{1, 3, 5\}\), find the complement \(A'\).
Start with the universe \(U = \{1, 2, 3, 4, 5, 6\}\).
The set \(A = \{1, 3, 5\}\) includes 1, 3, and 5.
The complement \(A'\) is all the elements in \(U\) that are not in \(A\):
$$A' = \{2, 4, 6\}$$
The set \(A = \{1, 3, 5\}\) includes 1, 3, and 5.
The complement \(A'\) is all the elements in \(U\) that are not in \(A\):
$$A' = \{2, 4, 6\}$$
Intersection and Union
Definition Intersection
The intersection of two sets \(A\) and \(B\), written \(A \cap B\), is the set of elements that are in both \(A\) and \(B\).
Example
What is the intersection \(\{1, 2, 3\} \cap \{2, 3, 4\}\)?
For the intersection \(\cap\), include all common element: \(\textcolor{colorprop}{2}\) \(\textcolor{olive}{3}\). Donc $$\{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3}\} \cap \{ \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\} = \{\textcolor{colorprop}{2},\textcolor{olive}{3}\}$$
Definition Union
The union of two sets \(A\) and \(B\), written \(A \cup B\), is the set of all elements in \(A\) or \(B\) (or both).
Example
What is the union \(\{1, 2, 3\} \cup \{2, 3, 4\}\)?
For the union \(\cup\), include all elements from both sets without repeats: \(\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\). So, $$\{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3}\} \cup \{ \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\} = \{\textcolor{colordef}{1}, \textcolor{colorprop}{2}, \textcolor{olive}{3},\textcolor{brown}{4}\}$$
Venn Diagrams
Definition Venn Diagram
A Venn diagram uses a rectangle to show the universal set \(U\) and circles to represent other sets within it.
Example
Here’s a Venn diagram for \(U = \{1, 2, 3, 4, 5, 6\}\) and \(A = \{1, 3, 5\}\):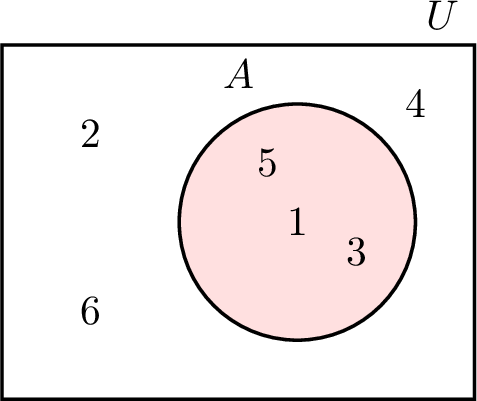

Definition Key Venn Diagram Concepts
This table shows common set operations and their Venn diagrams:
| Notation | Meaning | Venn Diagram |
| \(A\) | Set \(A\) | 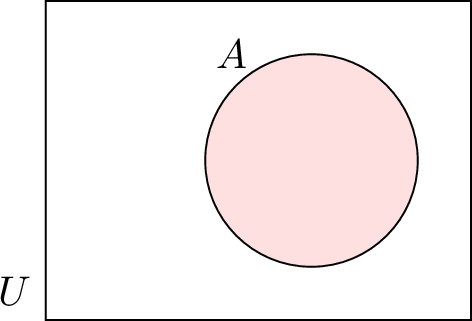 |
| \(A'\) | Complement of \(A\) (everything in \(U\) not in \(A\)) | 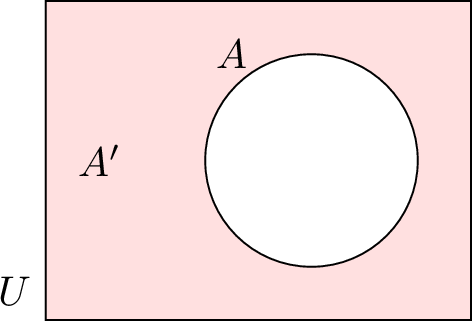 |
| \(A \subseteq B\) | \(A\) is a subset of \(B\) | 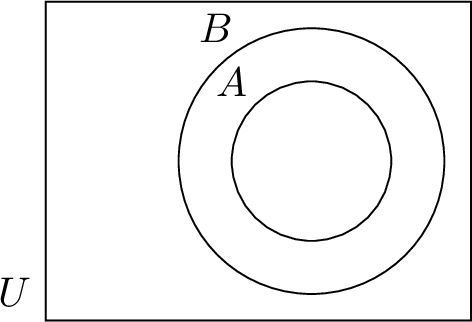 |
| \(A \cup B\) | Union of \(A\) and \(B\) (all elements in \(A\) or \(B\)) | 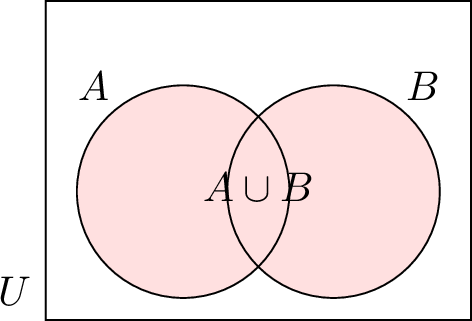 |
| \(A \cap B\) | Intersection of \(A\) and \(B\) (elements in both) | 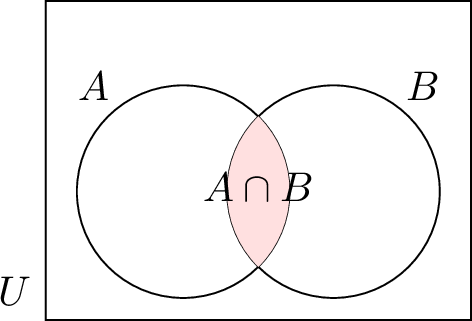 |
| \(A \cap B = \{\}\) | \(A\) and \(B\) are disjoint (no common elements) | 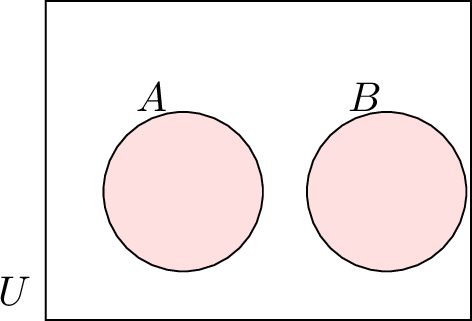 |
Venn diagrams help solve problems by showing the number of elements in each region.
Definition Counting Elements
In a Venn diagram, we use brackets around numbers to show how many elements are in each region.
Example
Consider this Venn diagram: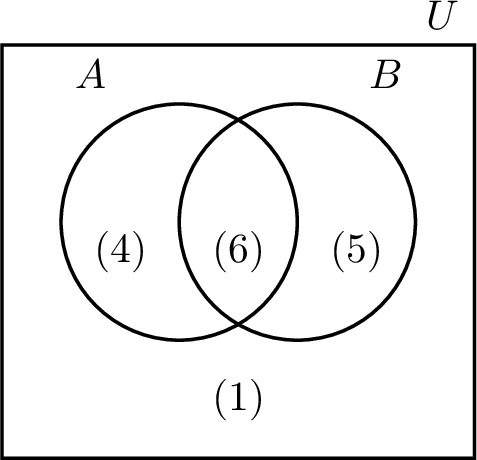

Number Sets
Common Number Sets
Number sets are groups of numbers defined by specific properties, and they form the foundation of mathematics. We start with the simplest set, the natural numbers (\(\N\)), which we use for basic counting. From there, we build the integers (\(\Z\)) by adding negative numbers to include opposites. Next, we expand to the rational numbers (\(\Q\)) by allowing fractions, which cover division between integers. Finally, we reach the real numbers (\(\R\)) by filling in all the gaps with irrational numbers, creating a complete number line. Below are the most common number sets you’ll encounter, each one growing from the previous set in this progression.
Definition Common Number Sets
- The natural numbers, denoted \(\N\), are the counting numbers starting from zero:$$\N = \{0, 1, 2, 3, 4, 5, 6, \dots\}$$
- The integers, denoted \(\Z\), include all whole numbers—positive, negative, and zero:$$\Z = \{\dots, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, \dots\}$$
- The rational numbers, denoted \(\Q\), are numbers that can be written as a fraction \(\frac{p}{q}\), where \(p\) and \(q\) are integers and \(q \neq 0\). Examples include \(\frac{1}{2}\), \(-3\), and \(\frac{5}{4}\):$$\Q = \left\{ \frac{p}{q} \mid p, q \in \Z, q \neq 0 \right\}$$
- The real numbers, denoted \(\R\), include all numbers on a continuous number line, such as rational numbers (like \(\frac{1}{3}\)) and irrational numbers (like \(\sqrt{2}\) and \(\pi\)):$$\R = \{\text{all numbers, rational and irrational}\}$$
Proposition Relationships Between Number Sets
The number sets are nested as follows:$$\N \subset \Z \subset \Q \subset \R$$This means every natural number is an integer, every integer is a rational number, and every rational number is a real number.
Intervals
Definition Interval
An interval is a set of all real numbers between two endpoints, which may or may not be included in the set.
Example
The set of all real numbers between 0 and 1, including 1 but not 0, is an interval. It is written as \(\{x \in \R \mid 0 < x \leq 1\}\).
Method Representing Intervals on a Number Line
Intervals are often shown on a number line using these conventions:
- An \emph{open circle} (or parenthesis) means the endpoint is not included.
- A \emph{filled circle} (or bracket) means the endpoint is included.
- An \emph{arrow} shows that the interval extends to positive or negative infinity.
Example
The number line representation of \(\{x \in \R \mid 0 < x \leq 1\}\) is:

Definition Interval notation
| Interval Notation | Set-builder notation | Number line representation |
| \(\CloseBracketLeft a, b \CloseBracketRight\) | \(\{x \in \R \mid a \leqslant x \leqslant b\}\) | |
| \(\CloseBracketLeft a, b \OpenBracketRight\) | \(\{x \in \R \mid a \leqslant x < b\}\) | |
| \(\OpenBracketLeft a, b \CloseBracketRight\) | \(\{x \in \R \mid a < x \leqslant b\}\) | |
| \(\OpenBracketLeft a, b \OpenBracketRight\) | \(\{x \in \R \mid a < x < b\}\) | |
| \(\CloseBracketLeft a, +\infty\OpenBracketRight \) | \(\{x \in \R \mid a \leqslant x\}\) | |
| \(\OpenBracketLeft a, +\infty \OpenBracketRight \) | \(\{x \in \R \mid a < x\}\) | |
| \(\OpenBracketLeft -\infty, a\CloseBracketRight\) | \(\{x \in \R \mid x \leqslant a\}\) | |
| \(\OpenBracketLeft -\infty, a\OpenBracketRight\) | \(\{x \in \R \mid x < a\}\) | |