Area
Definition
Definition Area
The area of a shape is the amount of space it covers on a flat surface. We measure it in square units, like square centimeters or square meters.
To find the area, imagine covering the shape with small squares, like tiles on a floor. Count how many squares fit inside the shape.
Example
Find the area of the red shape: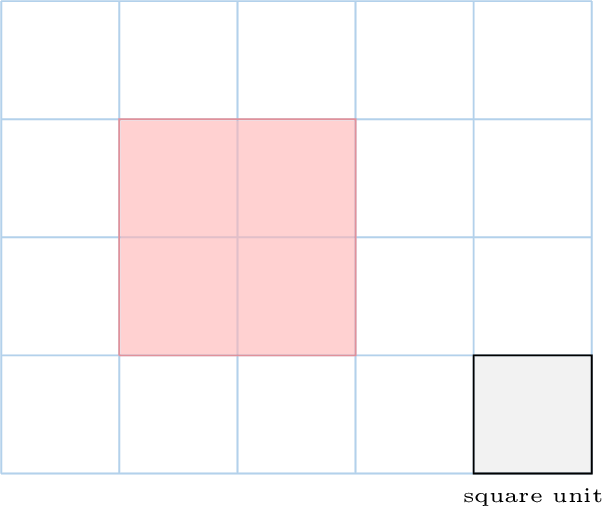

To find the area, we count the number of unit squares inside the shape.
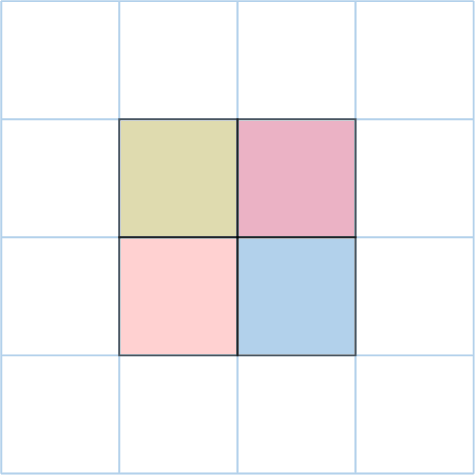
Units of Area
We can measure area using different units like tiles or paper squares. But these units are not the same for everyone. Your friend might have a bigger tile than yours, making it hard to compare. To solve this, mathematicians created universal units like the square centimeter and square meter, so everyone can measure and compare areas the same way.
Definition Units of Area
- Square Kilometer \(\left(\mathrm{km}^2\right)\): A very large unit of area, about the size of a small town.
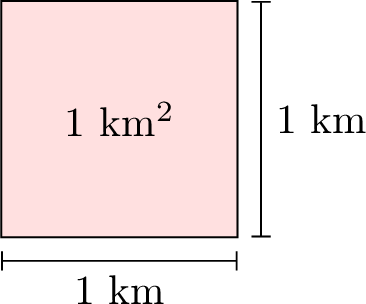
- Square Meter \(\left(\mathrm{m}^2\right)\): A larger unit of area, about the space it takes for you to lie down with your arms by your sides.
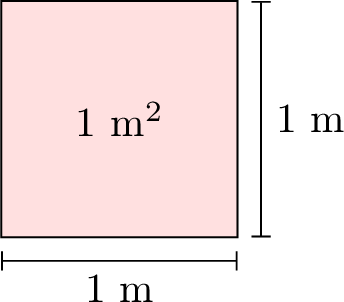
- Square Centimeter \(\left(\mathrm{cm}^2\right)\): A small unit of area, about the size of a big toe nail for a 6-year-old boy.
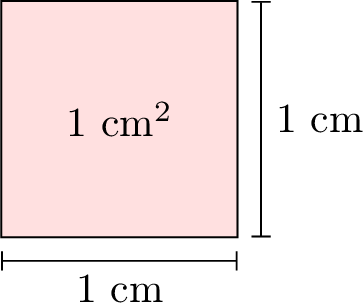
- Square Millimeter \(\left(\mathrm{mm}^2\right)\): A very small unit of area, about the size of a tiny dot made by a pencil.
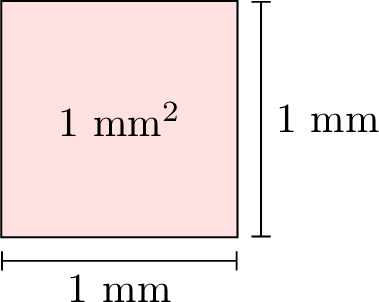
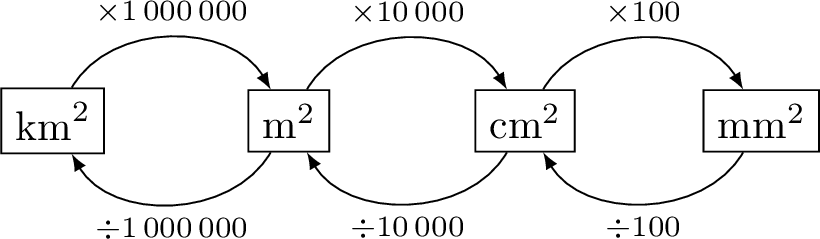
Conversion of Area Units
Let’s explore how area units are related by looking at a small square. Below is a square that measures 1 cm by 1 cm, which is 1 cm². We divide it into smaller squares, each 1 mm by 1 mm (1 mm²). Let’s count how many 1 mm² squares fit inside 1 cm².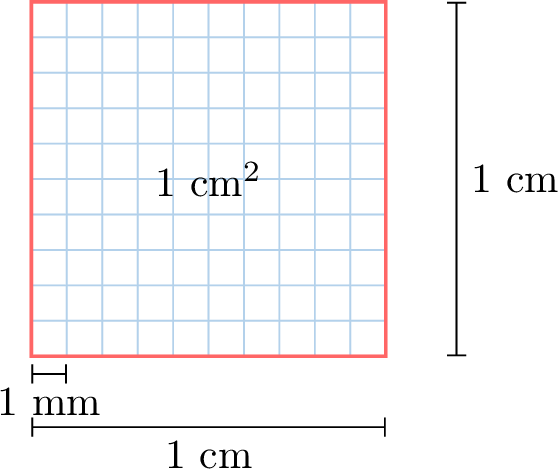

Proposition Conversion of Area Units
- \(1 \, \text{km}^2 = 1\,000\,000 \, \text{m}^2\)
- \(1 \, \text{m}^2 = 10\,000 \, \text{cm}^2\)
- \(1 \, \text{cm}^2 = 100 \, \text{mm}^2\)
Method Converting Using Multiplication or Division
- Use multiplication to go from a larger unit to a smaller one (like square meters to square centimeters).
- Use division to go from a smaller unit to a larger one (like square centimeters to square meters).
Method Converting Using a Table
To convert between units of area, we can use a conversion table. For example, to convert 10.5 square meters to square centimeters:
- Write the units in the table: km², m², cm², mm².

- Place the number in the column of the unit you start with.

- Fill in zeros in the columns to the right until you reach the unit you want to convert to.
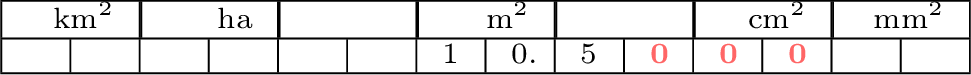
- Read the number in the column of the target unit.
So, 10.5 m² = \(10\,500\) cm².
Area of a Rectangle or a Square
To find the area of the rectangle: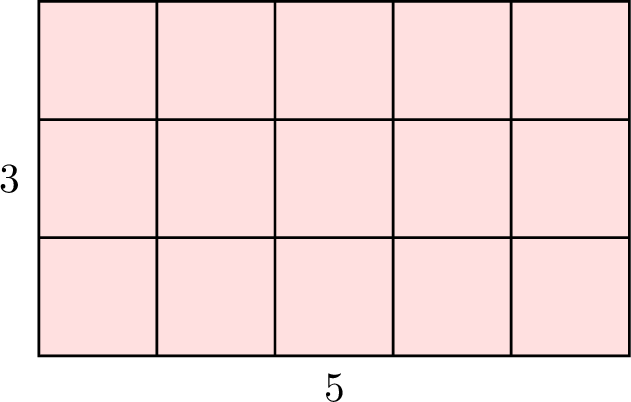

- Count the number of squares in each column:
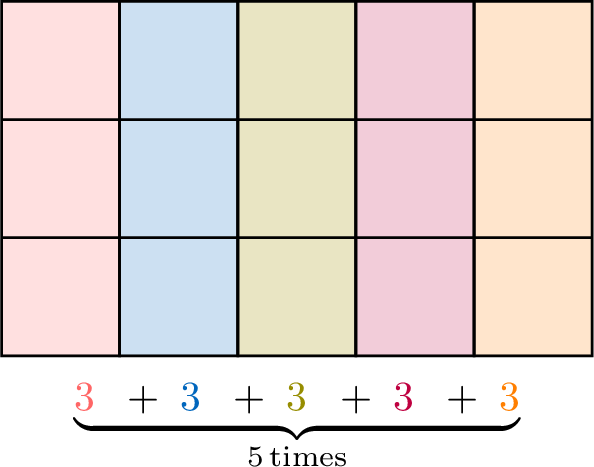
- Add them up: the area is \(\underbrace{\textcolor{colordef}{3}\;\;+\;\textcolor{colorprop}{3}\;\;+\;\textcolor{olive}{3}\;\;+\;\textcolor{purple}{3}\;\;+\;\textcolor{orange}{3}}_{5\,\text{times}} = 5 \times 3\). This shows that the area of the rectangle is found by multiplying the length by the width.
Proposition Area Formulas
| Name | Shape | Area |
| Rectangle | 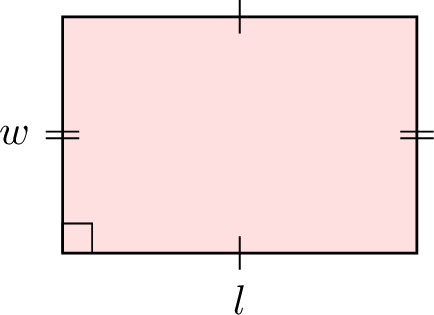 | \(l \times w\) |
| Square | 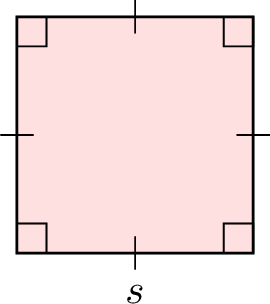 | \(s \times s\) |
Method Finding a Shape’s Area
To find the area of a rectangle or a square, multiply its length by its width.
Example
Find the area of the rectangle: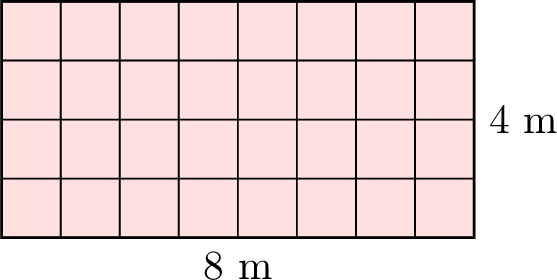

This is a rectangle with length \(L = 8\) m and width \(l = 4\) m. Using the formula for the area of a rectangle:$$\begin{aligned}[t]A &= L \times l \\&= 8 \times 4 \\&= 32 \, \mathrm{m}^2\end{aligned}$$So, the area is \(32\) square meters.
Area of a Triangle
To find the area of a triangle, we can cut it along its height to form two smaller triangles, then rearrange them to make a rectangle. Let’s see how this works step by step with the triangle below: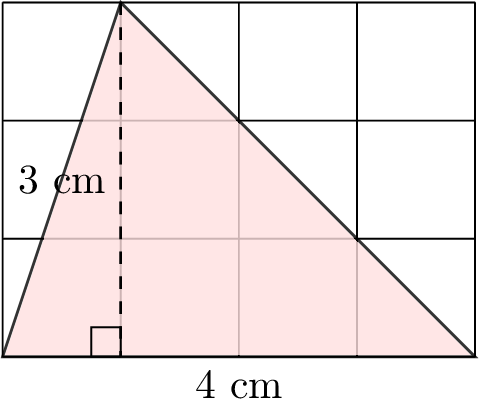

- Cut the triangle along the height to form two smaller triangles. Rotate and rearrange these triangles to form a rectangle:
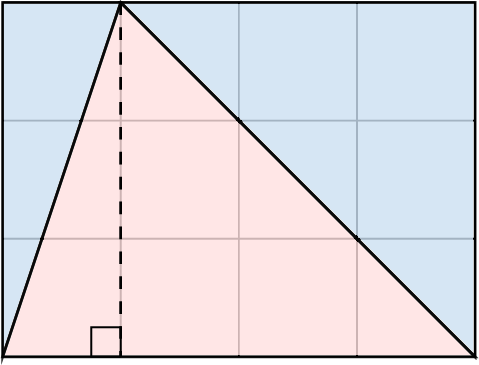
- The area of the rectangle is the length multiplied by the width: \(4 \times 3\). Since the area of the rectangle is equal to twice that of the original triangle, the area of the triangle is the area of the rectangle divided by two: \(\dfrac{4 \times 3}{2} = \dfrac{\text{base} \times \text{height}}{2}\).
Proposition Area of a Triangle
The area of a triangle is found by multiplying the base by the height and dividing by 2:$$\text{Area of a triangle} = \dfrac{\text{base} \times \text{height}}{2}$$$$A = \dfrac{b \times h}{2}$$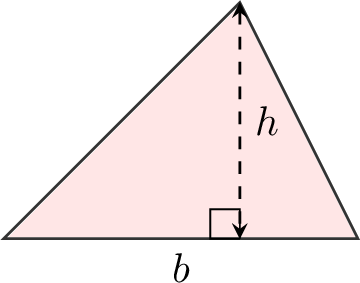

Example
Find the area of the triangle: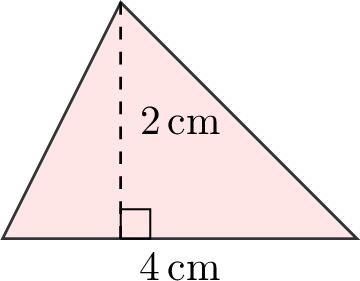

$$\begin{aligned}[t]A &= \dfrac{b \times h}{2} \\&= \dfrac{4 \times 2}{2} \\&= 4 \, \text{cm}^2\end{aligned}$$
Area of a Parallelogram
To find the area of a parallelogram, we can turn it into a rectangle by moving a triangle from one side to the other. Let’s see how this works step by step with the parallelogram below:

- Draw the height, which is a line from the top side to the bottom side that is perpendicular to the base:

- Cut the triangle on the right side:
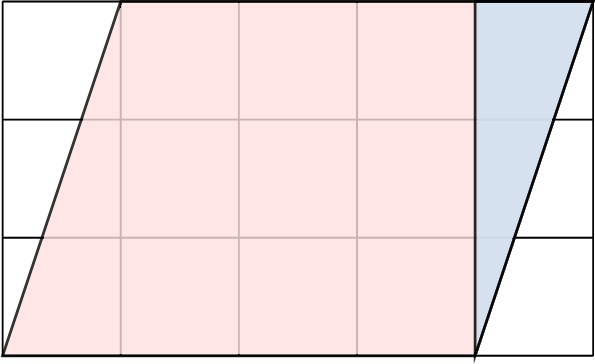
- Move the triangle to the left side to form a rectangle:
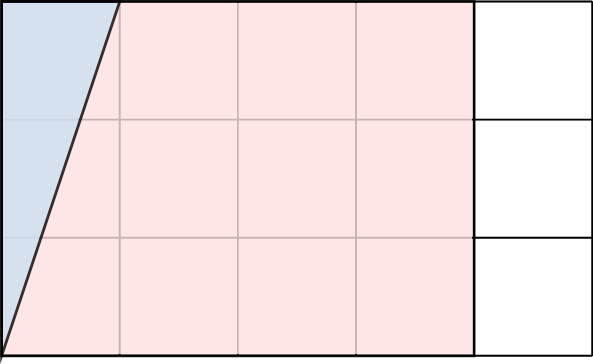
- Now we have a rectangle with a length (base) of 4 cm and a height of 3 cm. The area of the parallelogram is the same as the area of this rectangle, which is the base times the height: \(4 \times 3 = 12 \, \text{cm}^2\).
Proposition Area of a Parallelogram
The area of a parallelogram is found by multiplying the base by the height:$$\text{Area of a parallelogram} = \text{base} \times \text{height}$$$$A = b \times h$$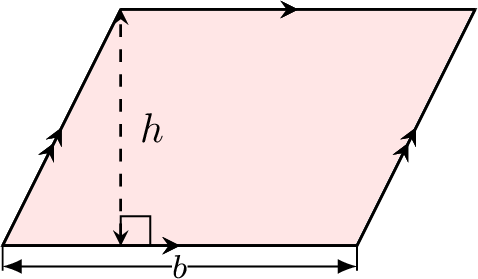

Example
Find the area of the parallelogram: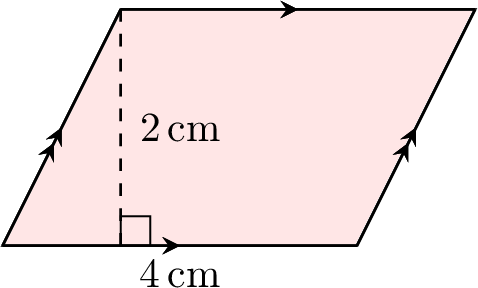

$$\begin{aligned}[t]A &= b \times h \\&= 4 \times 2 \\&= 8 \, \text{cm}^2\end{aligned}$$
Area of a Circle
To find the area of a circle, we can divide it into smaller parts and rearrange them to approximate a parallelogram. Let’s see how this works step by step:
- Divide the circle into 12 equal parts, like slices of a pie:
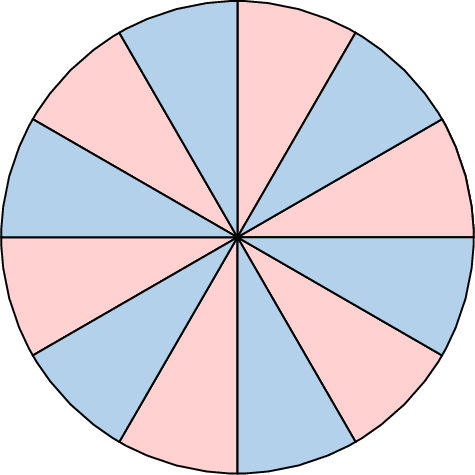
- Imagine cutting these 12 parts from the circle.
- Rearrange the parts by alternating them to form a shape that looks like a parallelogram:
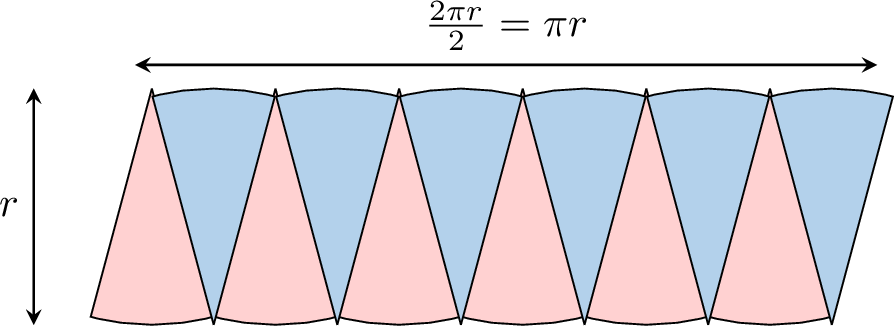
- The base of the parallelogram is approximately half the circumference of the circle (\(\pi r\)), and its height is approximately the radius (\(r\)). So, the area of the circle is the area of the parallelogram:$$\begin{aligned}A_\text{circle} &= (\pi r) \times r \\&= \pi \times r \times r \\\end{aligned}$$
Proposition Area of a Circle
The area of a circle is found by multiplying pi by the radius squared:$$\text{Area of a circle} = \pi \times \text{radius} \times \text{radius}$$$$A = \pi r \times r$$

Example
Find the area of the circle: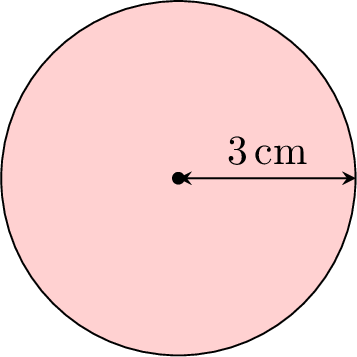

$$\begin{aligned}[t]A &= \pi r^2 \\&= \pi 3^2 \\&\approx 28.3 \, \text{cm}^2\end{aligned}$$
Area Formulas
Proposition Area Formulas
| Name | Shape | Area |
| Rectangle |  | \(A = l \times w\) |
| Square | 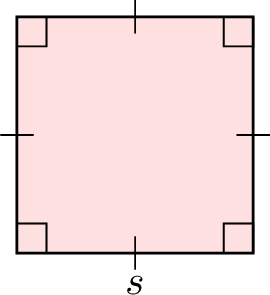 | \(\begin{aligned}A &= s \times s \\&= s^2\end{aligned}\) |
| Parallelogram | 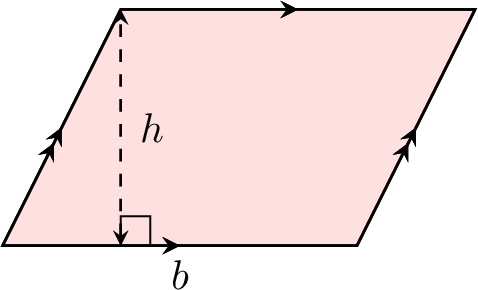 | \(A = b \times h\) |
| Triangle | 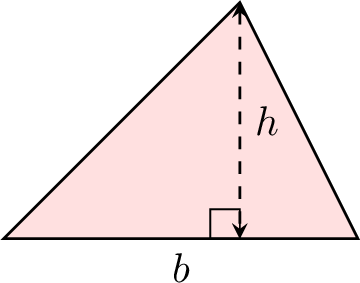 | \(A = \dfrac{b \times h}{2}\) |
| Circle |  | \(\begin{aligned}A &= \pi \times r \times r \\&= \pi r^2\end{aligned}\) |
Area of Composite Figures
Definition Composite Figure
A composite figure is made up of two or more simple geometric shapes, like rectangles, triangles, or circles, combined together.
Method Finding the Area of a Composite Figure
To find the area of a composite figure, follow these steps:
- Divide the figure into simple, non-overlapping shapes, such as rectangles, triangles, or circles.
- Find the area of each simpler shape using the appropriate formula.
- Add the areas together to find the total area of the composite figure.
Example
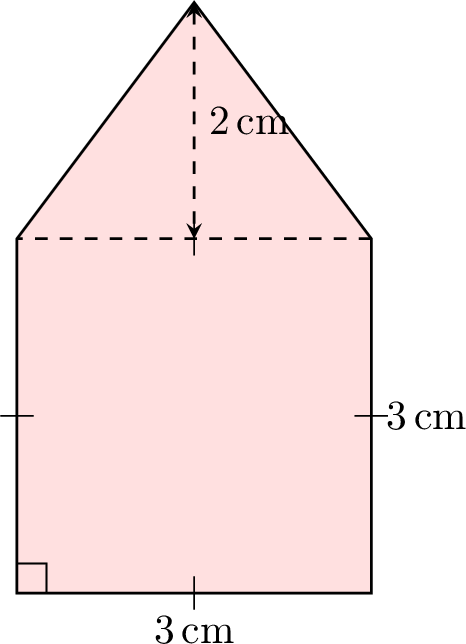
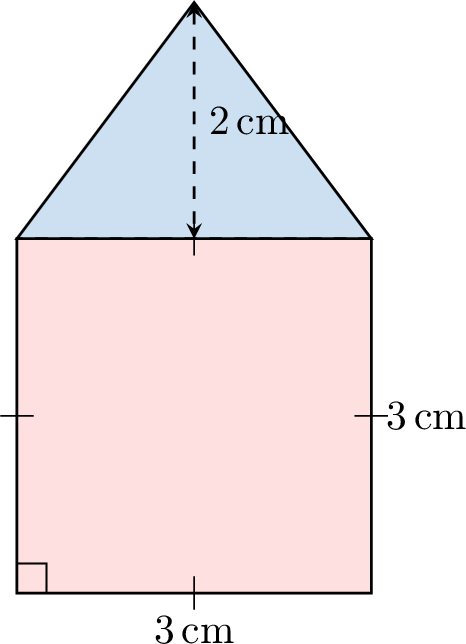
Find the area of the composite figure below, which is made up of a square and a triangle: