Length
Length Units
We can measure length using different units like blocks or erasers. But these units are not the same for everyone. Your friend might have a longer eraser than yours, making it hard to compare. To solve this, mathematicians created a universal unit called the meter, so everyone can measure and compare lengths the same way.
Definition Units of Length
- Millimeter \(\left(\mathrm{mm}\right)\): A very small unit of length, about the thickness of a coin.

- Centimeter \(\left(\mathrm{cm}\right)\): A small unit of length, about the width of your finger.
- Meter \(\left(\mathrm{m}\right)\): A longer unit of length, about the height of a 6-year-old girl.

- Kilometer \(\left(\mathrm{km}\right)\): A very long unit of length, about the height of the Burj Khalifa in Dubai, United Arab Emirates.

Conversion of Length Units
Definition Conversion of Length Units
- \(1\text{ km}=1000\text{ m}\)
- \(1\text{ m}=100\text{ cm}\)
- \(1\text{ cm}=10\text{ mm}\)
Method Converting using a Multiplication or a Division
- Use multiplication to go from a bigger unit to a smaller one (like meters to centimeters).
- Use division to go from a smaller unit to a bigger one (like centimeters to meters).
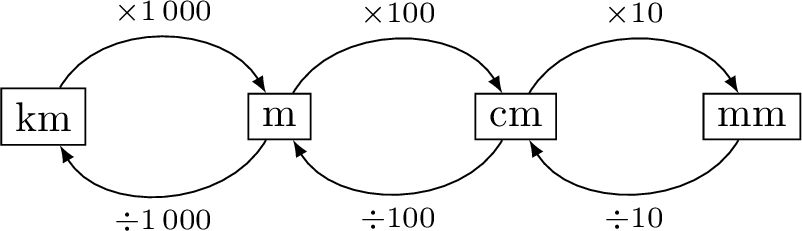
Method Converting Using a Table
To convert between units of length, we can use a conversion table. For example, to convert 1.2 meters to centimeters:
- Write the units in the table: km, m, cm, mm.
\(\mathrm{km}\) \(\quad\;\) \(\quad\;\) \(\;\mathrm{m}\) \(\quad\;\) \(\mathrm{cm}\) \(\mathrm{mm}\) - Place the number in the column of the unit you start with.
\(\mathrm{km}\) \(\quad\;\) \(\quad\;\) \(\;\mathrm{m}\) \(\quad\;\) \(\mathrm{cm}\) \(\mathrm{mm}\) 1. 2 - Fill in zeros in the columns to the right until you reach the unit you want to convert to.
\(\mathrm{km}\) \(\quad\;\) \(\quad\;\) \(\;\mathrm{m}\) \(\quad\;\) \(\mathrm{cm}\) \(\mathrm{mm}\) 1. 2 0 - Read the number in the column of the target unit
So, 1.2 m = 120 cm.
Perimeter
Definition Perimeter
The perimeter of a shape is the total length around its outside edge.
To find the perimeter, imagine walking around the shape like it’s a park. Count the number of unit lengths along each side as you go.
Example
Find the perimeter of the red shape: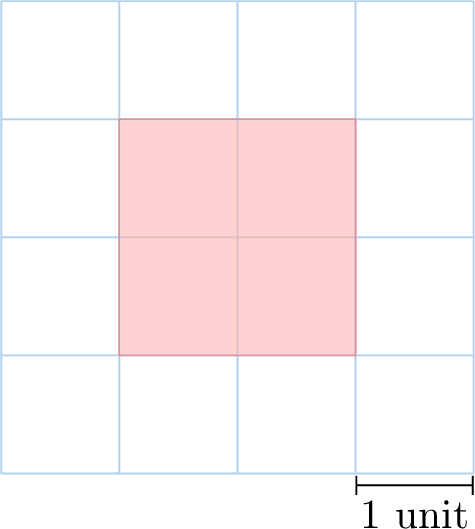

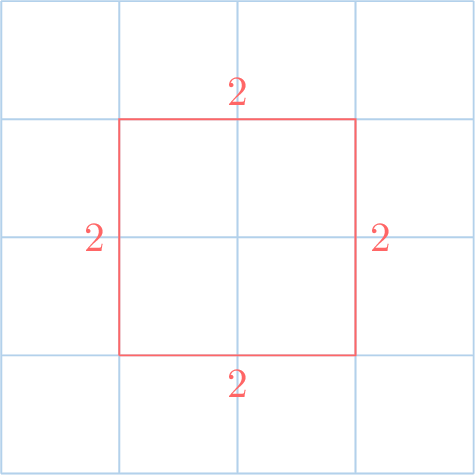
The perimeter is 8 units.
Perimeter of Common Shapes
Method Finding a Polygon’s Perimeter
To find the perimeter of any polygon (a shape with straight sides), add up the lengths of all its sides.
Proposition Perimeter Formulas
| Name | Shape | Perimeter |
| Triangle | 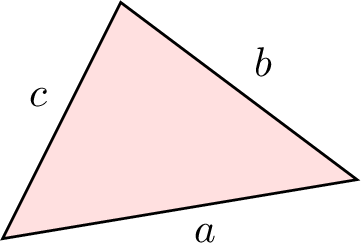 | \(a + b + c\) |
| Rectangle | 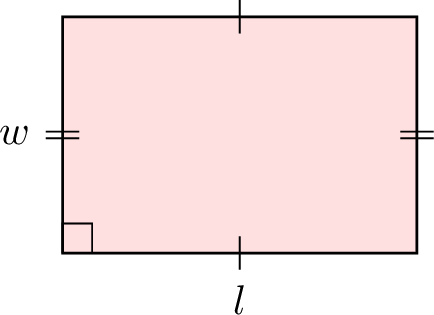 | \(l+w+l+w= (2\times l) + (2\times w) \) |
| Square | 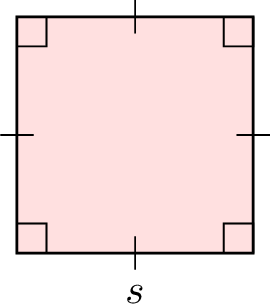 | \(s+s+s+s=4\times s\) |
| Circle | 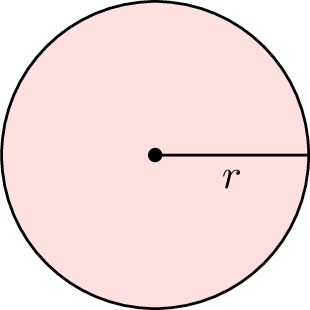 | \(2\times \pi \times r\) |
Example
Find the perimeter of the rectangle: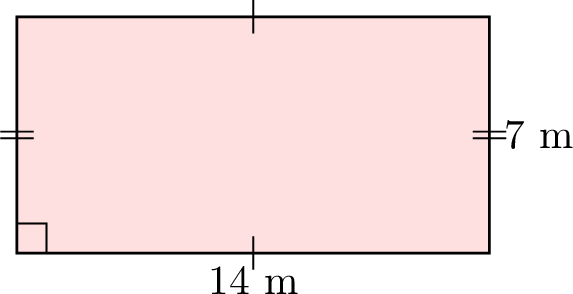

This is a rectangle with length \(l = 14\) m and width \(w = 7\) m. Using the formula for the perimeter of a rectangle:$$\begin{aligned}[t]P &= (2\times l) + (2\times w) \\&= (2 \times 14) + (2 \times 7) \\&= 28 + 14 \\&= 42 \, \mathrm{m}\end{aligned}$$So, the perimeter is \(42\) meters.
Length of an Arc
Definition Arc of a Circle
An arc is a part of the circumference of a circle. The length of an arc depends on the angle it makes at the center of the circle.
Example
A quarter circle (90 degrees) has an arc that is one-fourth of the full circumference.

Method Finding the Length of an Arc
To find the length of an arc of a circle:
- Determine the fraction of the circle that the arc represents by dividing the arc’s central angle by 360 degrees: Fraction = \(\frac{\text{central angle}}{360}\).
- Multiply the full circumference by the fraction to find the arc length: Arc length = Fraction \(\times\) Circumference.
Example
Find the length of the arc of circle

- Determine the fraction of the circle that the arc represents:$$\begin{aligned}\text{Fraction} &= \frac{\text{central angle}}{360} \\&= \frac{90}{360} \\&= \frac{1}{4}\end{aligned}$$
- Multiply the full circumference by the fraction to find the arc length:$$\begin{aligned}\text{Arc length} &= \text{Fraction} \times \text{Circumference} \\&= \frac{1}{4} \times 2\times \pi \times 4 \\&\approx 6.3 \, \text{cm} \quad \text{(use calculator)} \\\end{aligned}$$
Perimeter of Composite Figures
Definition Composite Figure
A composite figure is a shape made up of two or more simple shapes, like triangles, rectangles, or squares, combined together.
Method Finding the Perimeter of a Composite Figure
To find the perimeter of a composite figure:
- Identify all the outer sides of the shape.
- Add the lengths of these outer sides together to find the total perimeter.
Example
Find the perimeter of the composite figure:

\(P=\)
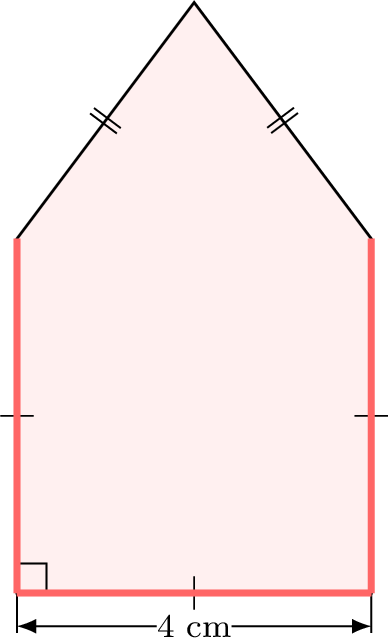 +
+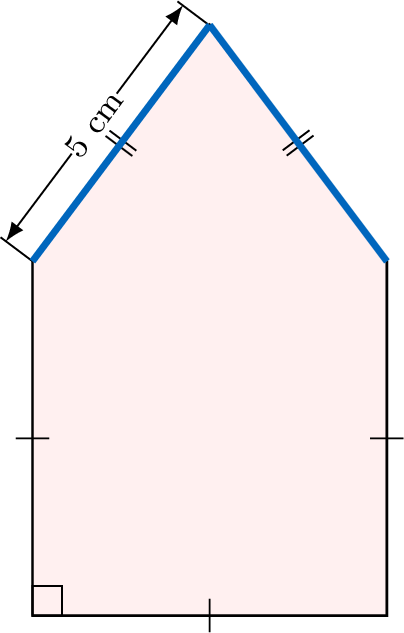
\(\begin{aligned}[t]P &= \textcolor{colordef}{3\times 4 \mathrm{~cm}} + \textcolor{colorprop}{2\times 5 \mathrm{~cm}}\\P &= 22 \mathrm{~cm}\\\end{aligned}\)