Probability
Ever wondered if it'll rain tomorrow or if you'll win a game? That's probability! It's a math way to guess how likely things are to happen.
Outcome
Definition Outcome
An outcome is one possible result of a random experiment.
Definition All Possible Outcomes
All possible outcomes are the complete list of everything that could happen in a random experiment.
Example
What are all the possible outcomes when you flip a coin? 
All possible outcomes are Heads (H) and Tails (T).
Example
What are all the possible outcomes when you roll a six-sided die?
All possible outcomes are 1= ,2=
,2=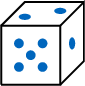 ,3=
,3=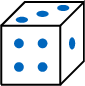 ,4=
,4= ,5=
,5=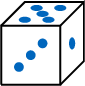 ,and 6=
,and 6=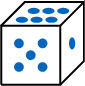 .
.
Event
Definition Event
An event is a set of outcomes from all possible outcomes.
Example
In the experiment of rolling a die, find the outcomes that correspond to rolling a number greater than 4.
The outcomes for "rolling an even number" are 2= ,4=
,4= ,and 6=
,and 6= .
.
Using Words to Describe Probability
We often use words to talk about probability. If something will never happen, it's impossible. If it will definitely happen, it's certain. In between, we say things like 'likely,' '50-50 chance,' or 'unlikely.' We can line them up from least to most likely.
Definition Probability Line

- Impossible: It can’t happen.
Example: Riding a dinosaur. - Less likely: It probably won’t happen.
Example: Rolling a die and getting a 3. - Even chance: It has the same chance to happen or not.
Example: Tossing a coin and getting head. - Most likely: It will probably happen.
Example: Smiling at school today. - Certain: It will happen.
Example: The sun will rise tomorrow.
Using Numbers to Quantify Probability
When you flip a coin, there are two possible outcomes: heads or tails. The chance of getting heads is the same as getting tails—it’s 1 out of 2! In math, we write:


Definition Probability
The probability of an event, written \(P(\text{event})\), is a number that tells us how likely the event is to happen. It's always between 0 (impossible) and 1 (certain).

Expressing Probabilities in Different Forms
Method Expressing Probabilities in Different Forms
Probabilities can be expressed in multiple forms, such as fractions, decimals, or percentages, depending on the context or preference. Each form provides the same information but in a different representation, making it easier to understand or compare likelihoods.
Example
The probability of an event "even chance" can be represented as:
- Fraction: \( \frac{1}{2} \)
- Decimal: To convert the fraction to a decimal, divide the numerator by the denominator: \( 1 \div 2 = 0.5 \).
- Percentage: To convert the decimal to a percentage, multiply by 100: \( 0.5 \times 100 = 50\pourcent \).
Calculating Probabilities
In some experiments, every outcome is equally likely to occur, such as when flipping a fair coin or olling a fair die. These are referred to as equally likely outcomes.
Definition Equally Likely
When all outcomes are equally likely, the probability of an event is given by the formula:$$P(\text{event}) = \frac{\text{number of outcomes in the event}}{\text{total number of possible outcomes}}$$
Example
Calculate the probability of rolling an even number with a fair six-sided die.
- The total number of possible outcomes when rolling a fair six-sided die is 6, since there are 6 faces.
- The number of outcomes for the event "even number" is 3, as there are three even numbers on the die: 2, 4, and 6.
- Therefore, the probability of rolling an even number is given by:$$\begin{aligned}P(\text{even number}) &= \frac{\text{number of outcomes in the event}}{\text{total number of possible outcomes}} \\&= \frac{3}{6} \\&= \frac{1}{2}\end{aligned}$$
Experimental Probability
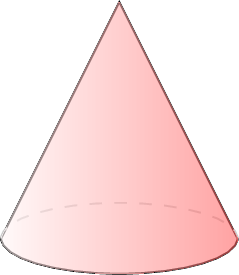
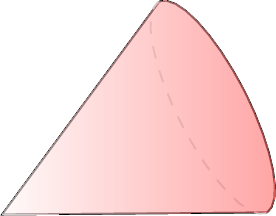
Isaac wishes to determine how a cone lands when tossed—base down or point down? The possible outcomes are as follows:
- Base down:
- Point down:
- Base down: 30 times.
- Point down: 20 times.
- \( P(\text{"base down"}) = \frac{30}{50} = 0.6 \) (60\(\pourcent\)).
- \( P(\text{"point down"}) = \frac{20}{50} = 0.4 \) (40\(\pourcent\)).
Theorem Law of Large Numbers
The probability of an event, \( P(\text{event}) \), can be estimated using the formula:$$P(\text{event}) \approx \frac{\text{number of times the event occurs}}{\text{number of trials}}$$Here, "trials" refer to the number of times the experiment is repeated.