Area Formulas
Area of a Rectangle or a Square
To find the area of the rectangle: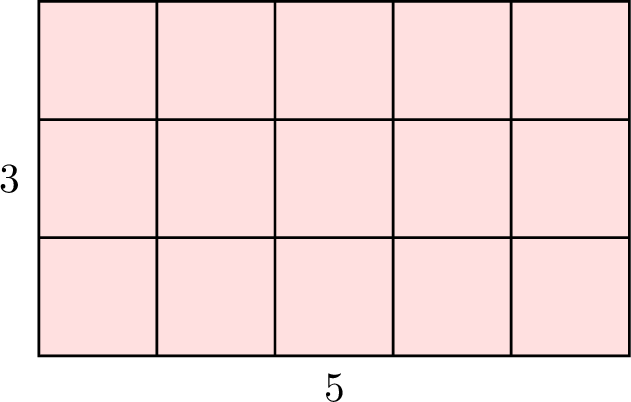

- Count the number of squares in each column:
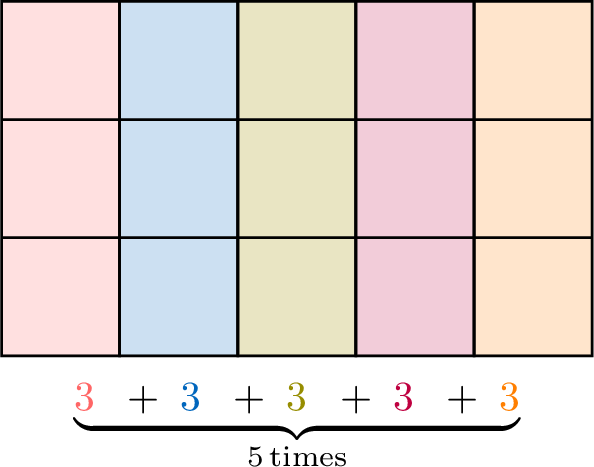
- Add them up: the area is \(\underbrace{\textcolor{colordef}{3}\;\;+\;\textcolor{colorprop}{3}\;\;+\;\textcolor{olive}{3}\;\;+\;\textcolor{purple}{3}\;\;+\;\textcolor{orange}{3}}_{5\,\text{times}} = 5 \times 3\). This shows that the area of the rectangle is found by multiplying the length by the width.
Proposition Area Formulas
| Name | Shape | Area |
| Rectangle | 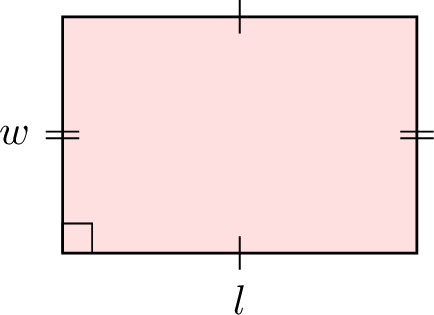 | \(l \times w\) |
| Square | 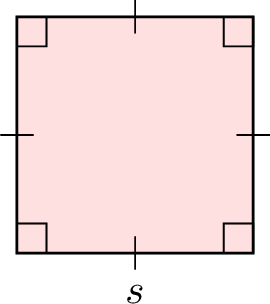 | \(s \times s\) |
Method Finding a Shape’s Area
To find the area of a rectangle or a square, multiply its length by its width.
Example
Find the area of the rectangle: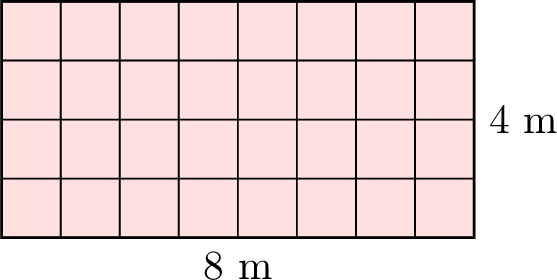

This is a rectangle with length \(L = 8\) m and width \(l = 4\) m. Using the formula for the area of a rectangle:$$\begin{aligned}[t]A &= L \times l \\&= 8 \times 4 \\&= 32 \, \mathrm{m}^2\end{aligned}$$So, the area is \(32\) square meters.
Area of a Triangle
To find the area of a triangle, we can cut it along its height to form two smaller triangles, then rearrange them to make a rectangle. Let’s see how this works step by step with the triangle below: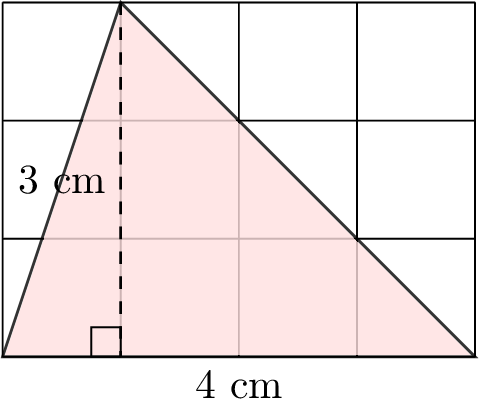

- Cut the triangle along the height to form two smaller triangles. Rotate and rearrange these triangles to form a rectangle:
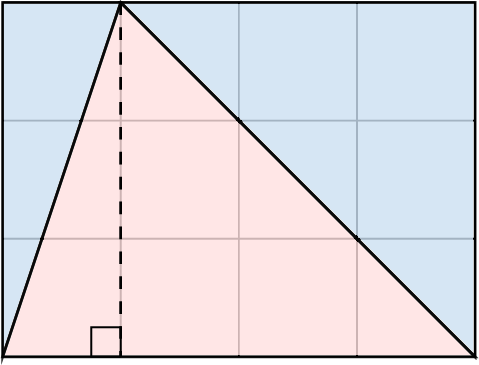
- The area of the rectangle is the length multiplied by the width: \(4 \times 3\). Since the area of the rectangle is equal to twice that of the original triangle, the area of the triangle is the area of the rectangle divided by two: \(\dfrac{4 \times 3}{2} = \dfrac{\text{base} \times \text{height}}{2}\).
Proposition Area of a Triangle
The area of a triangle is found by multiplying the base by the height and dividing by 2:$$\text{Area of a triangle} = \dfrac{\text{base} \times \text{height}}{2}$$$$A = \dfrac{b \times h}{2}$$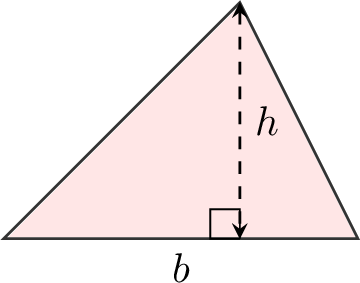

Example
Find the area of the triangle: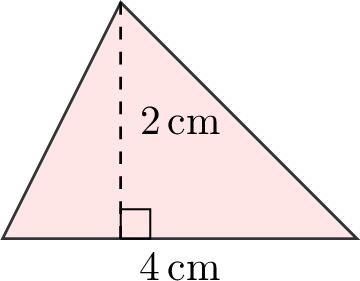

$$\begin{aligned}[t]A &= \dfrac{b \times h}{2} \\&= \dfrac{4 \times 2}{2} \\&= 4 \, \text{cm}^2\end{aligned}$$
Area of a Parallelogram
To find the area of a parallelogram, we can turn it into a rectangle by moving a triangle from one side to the other. Let’s see how this works step by step with the parallelogram below:

- Draw the height, which is a line from the top side to the bottom side that is perpendicular to the base:

- Cut the triangle on the right side:
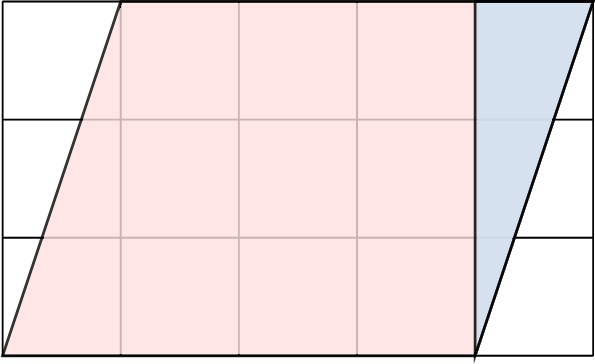
- Move the triangle to the left side to form a rectangle:
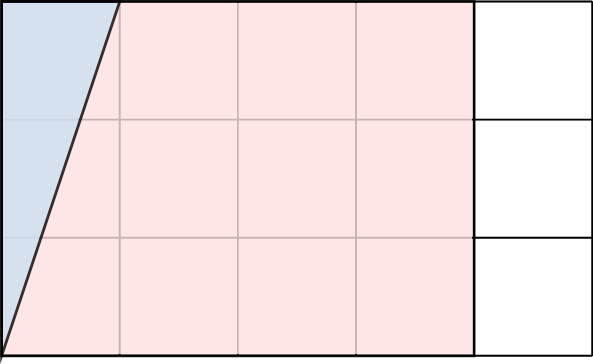
- Now we have a rectangle with a length (base) of 4 cm and a height of 3 cm. The area of the parallelogram is the same as the area of this rectangle, which is the base times the height: \(4 \times 3 = 12 \, \text{cm}^2\).
Proposition Area of a Parallelogram
The area of a parallelogram is found by multiplying the base by the height:$$\text{Area of a parallelogram} = \text{base} \times \text{height}$$$$A = b \times h$$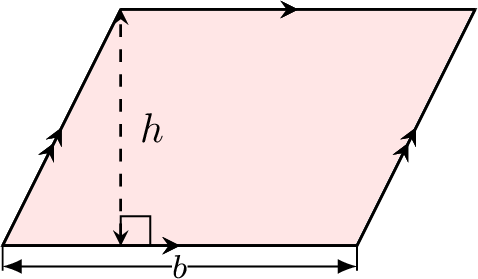

Example
Find the area of the parallelogram: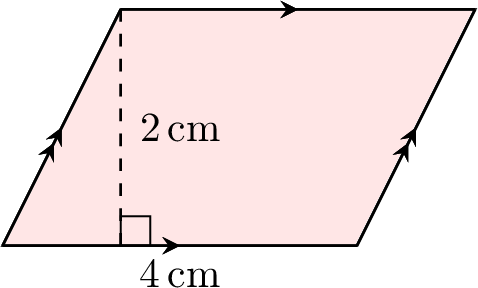

$$\begin{aligned}[t]A &= b \times h \\&= 4 \times 2 \\&= 8 \, \text{cm}^2\end{aligned}$$
Area of a Circle
To find the area of a circle, we can divide it into smaller parts and rearrange them to approximate a parallelogram. Let’s see how this works step by step:
- Divide the circle into 12 equal parts, like slices of a pie:
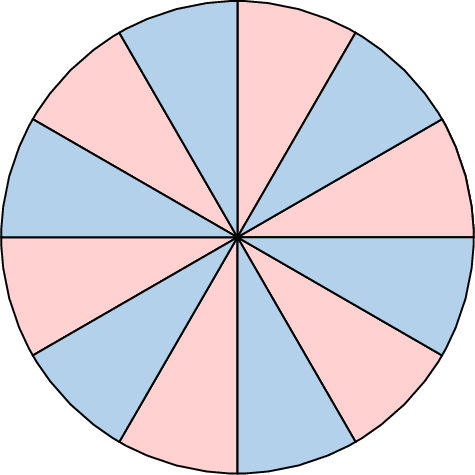
- Imagine cutting these 12 parts from the circle.
- Rearrange the parts by alternating them to form a shape that looks like a parallelogram:
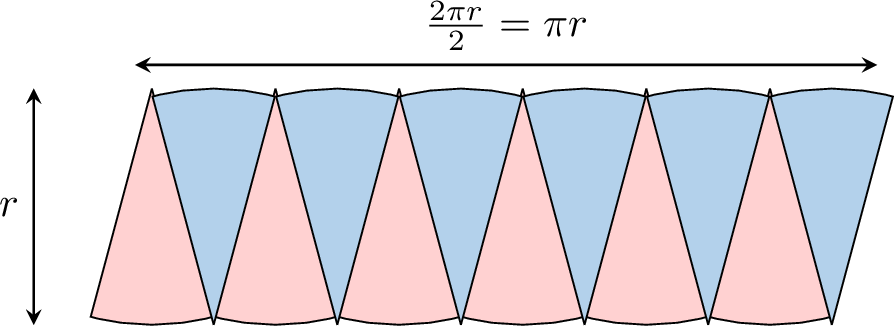
- The base of the parallelogram is approximately half the circumference of the circle (\(\pi r\)), and its height is approximately the radius (\(r\)). So, the area of the circle is the area of the parallelogram:$$\begin{aligned}A_\text{circle} &= (\pi r) \times r \\&= \pi \times r \times r \\\end{aligned}$$
Proposition Area of a Circle
The area of a circle is found by multiplying pi by the radius squared:$$\text{Area of a circle} = \pi \times \text{radius} \times \text{radius}$$$$A = \pi r \times r$$

Example
Find the area of the circle: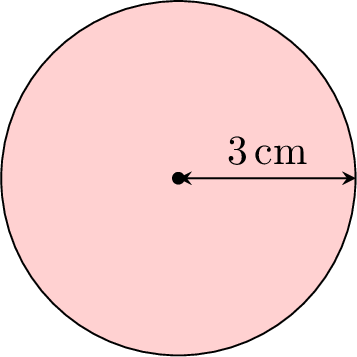

$$\begin{aligned}[t]A &= \pi \times r \times r \\&= \pi \times 3 \times 3 \\&\approx 28.3 \, \text{cm}^2\end{aligned}$$
Area Formulas
Proposition Area Formulas
| Name | Shape | Area |
| Rectangle |  | \(A = l \times w\) |
| Square | 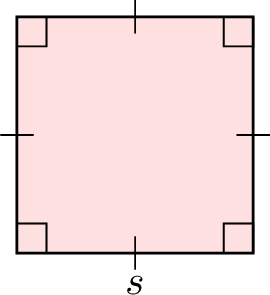 | \(\begin{aligned}A &= s \times s \\&= s^2\end{aligned}\) |
| Parallelogram | 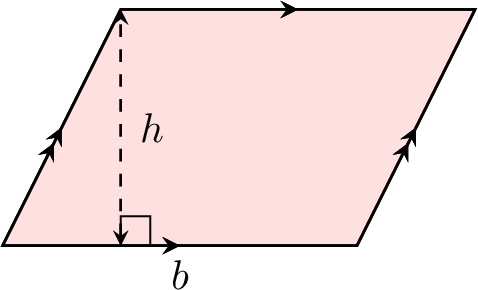 | \(A = b \times h\) |
| Triangle | 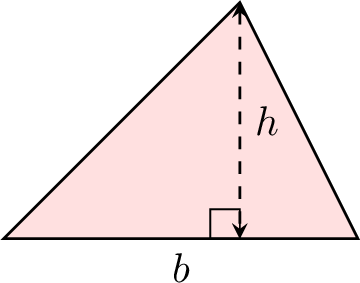 | \(A = \dfrac{b \times h}{2}\) |
| Circle |  | \(\begin{aligned}A &= \pi \times r \times r \\&= \pi r^2\end{aligned}\) |
Area of Composite Figures
Definition Composite Figure
A composite figure is made up of two or more simple geometric shapes, like rectangles, triangles, or circles, combined together.
Method Finding the Area of a Composite Figure
To find the area of a composite figure, follow these steps:
- Divide the figure into simple, non-overlapping shapes, such as rectangles, triangles, or circles.
- Find the area of each simpler shape using the appropriate formula.
- Add the areas together to find the total area of the composite figure.
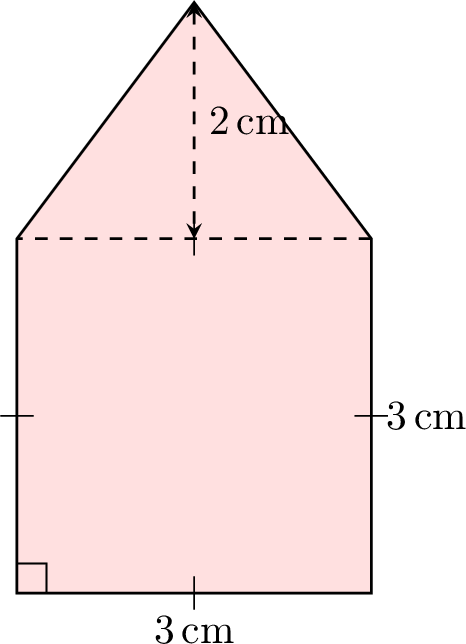
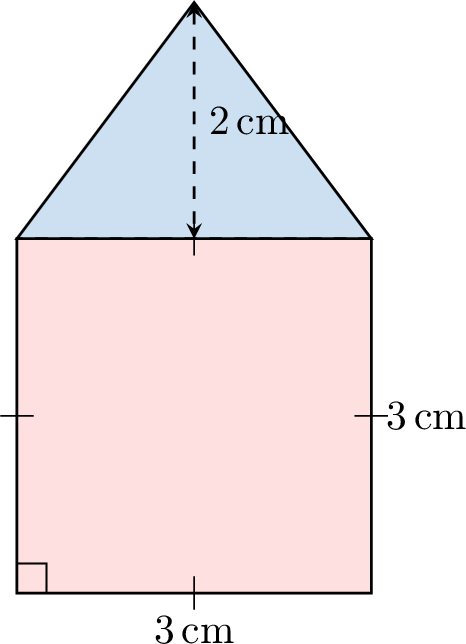
Example
Find the area of the composite figure below, which is made up of a square and a triangle: