Ratio
Definition
Definition Ratio
A ratio is a comparison of two quantities. The ratio \(\textcolor{colordef}{3}\) to \(\textcolor{colorprop}{2}\) can be expressed as \(\textcolor{colordef}{3}:\textcolor{colorprop}{2}\) or \(\dfrac{\textcolor{colordef}{3}}{\textcolor{colorprop}{2}}\).
Part-Part Ratios
Definition Part-Part Ratio
A part-part ratio compares two distinct parts of a whole.$$\textcolor{colordef}{\text{Part 1}}:\textcolor{colorprop}{\text{Part 2}}$$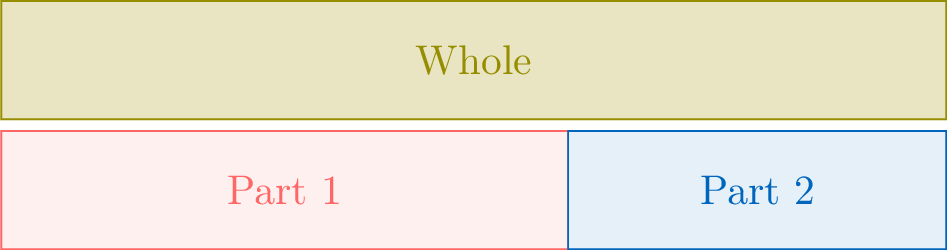

Example
For one bowl of fruit juice, there are \(\textcolor{colordef}{3}\) cherries and \(\textcolor{olive}{2}\) apples.

Part-Whole Ratios
Definition Part-Whole Ratio
A Part-whole ratio compares one part of a whole to the whole.$$\textcolor{colordef}{\text{Part 1}}:\textcolor{olive}{\text{Whole}}\text{ or }\textcolor{colorprop}{\text{Part 2}}:\textcolor{olive}{\text{Whole}}$$

Example
If a juice is made with \(\textcolor{yellow}{1}\) lemon and \(\textcolor{orange}{2}\) oranges, find the ratio of oranges to the total number of fruits.
- The total number of fruits is \(\textcolor{yellow}{1}+\textcolor{orange}{2} = 3\).
- The ratio of oranges to the total number of fruits is \(\textcolor{orange}{2}:3\) or \(\dfrac{\textcolor{orange}{2}}{3}\).
Equivalent Ratios
The ratio of red apples to all apples is \(\dfrac{2}{4}\), which can be simplified to \(\dfrac{1}{2}\) (half of the apples are red). 

Definition Equivalent Ratios
Two ratios are equal if one can be expressed as a multiple of the other.
Method Using Fractions
To show that two ratios are equal, we can compare their related fractions. If the fractions are equal, then the ratios are equal.
Example
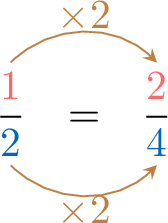 , \(\textcolor{colordef}{1}:\textcolor{colorprop}{2}=\textcolor{colordef}{2}:\textcolor{colorprop}{4}\)
, \(\textcolor{colordef}{1}:\textcolor{colorprop}{2}=\textcolor{colordef}{2}:\textcolor{colorprop}{4}\)Proportion
- For one glass of juice, you need \(\textcolor{colordef}{1}\) lemon and \(\textcolor{colorprop}{2}\) oranges. The ratio of lemons to oranges is \(\textcolor{colordef}{1}:\textcolor{colorprop}{2}\).

- To make two glasses of juice, double the ingredients: \(\textcolor{colordef}{2}\) lemons and \(\textcolor{colorprop}{4}\) oranges.

- The juices are in proportion because the ratios are equivalent: \(\dfrac{\textcolor{colordef}{1}}{\textcolor{colorprop}{2}} = \dfrac{\textcolor{colordef}{2}}{\textcolor{colorprop}{4}}\).
Definition Proportion
A proportion is an equation stating that two ratios are equivalent.
Example
To make \(\textcolor{colorprop}{1}\) chocolate cake, you need \(\textcolor{colordef}{4}\) eggs. How many eggs are needed for \(\textcolor{colorprop}{2}\) cakes?
For \(\textcolor{colorprop}{1}\) cake, you need \(\textcolor{colordef}{4}\) eggs. To find the number of eggs for \(\textcolor{colorprop}{2}\) cakes, set up a proportion: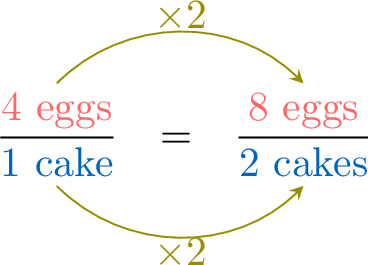
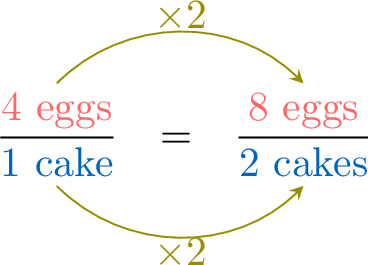
Part in Whole-Part Relationships
Method Finding Part in Whole-Part Relationships
To find the number of apples corresponding to \(\dfrac{1}{2}\) of 4 apples:

- Draw the fraction:

- Count the apples in the colored part: there are 2 apples.