Volume
Definition
Definition Volume
The volume of a shape is the amount of space it takes up in three dimensions. We measure it in cubic units, like cubic centimeters or cubic meters.
To find the volume, imagine filling the shape with small cubes, like building blocks. Count how many cubes fit inside the shape.
Example
Find the volume: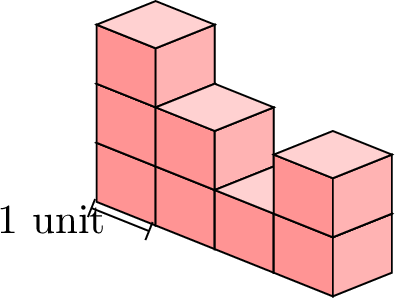
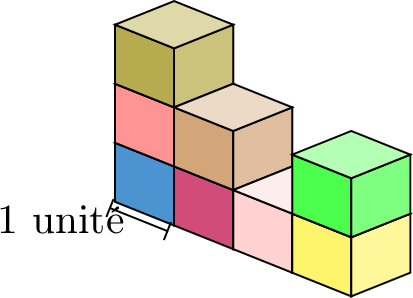
Units of Volume
We can measure volume using different units like blocks or small boxes. But these units are not the same for everyone. Your friend might have a bigger block than yours, making it hard to compare. To solve this, mathematicians created universal units like the cubic centimeter and cubic meter, so everyone can measure and compare volumes the same way.
Definition Units of Volume
- Cubic Centimeter \(\left(\mathrm{cm}^3\right)\): A small unit of volume, about the size of a small ice cube.
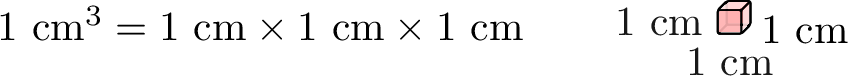
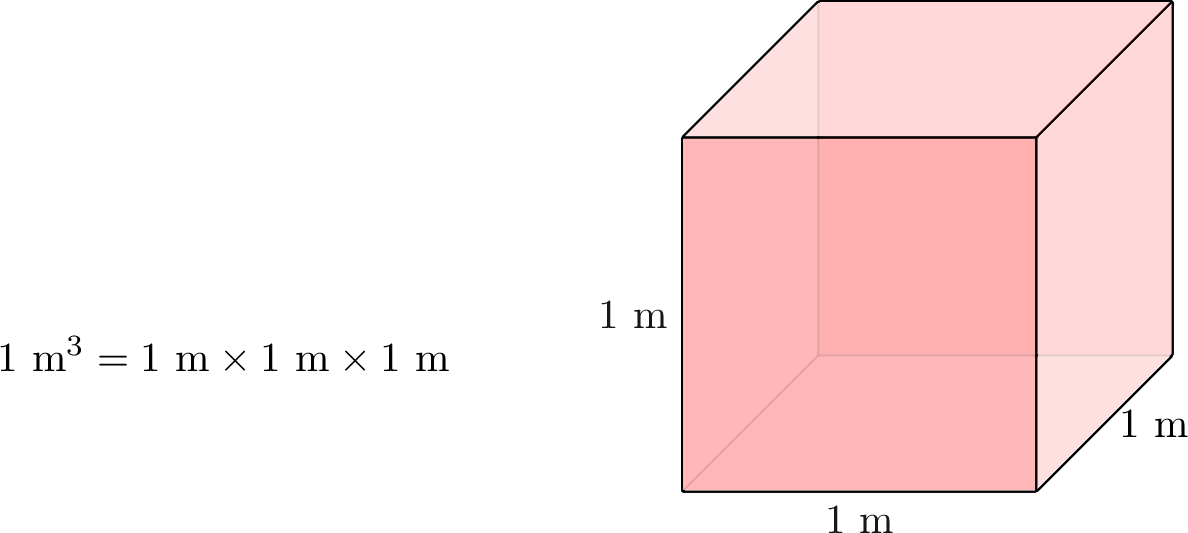
- Cubic Meter \(\left(\mathrm{m}^3\right)\): A larger unit of volume, about the space it takes for a washing machine.
Volume of a Rectangular Cuboid
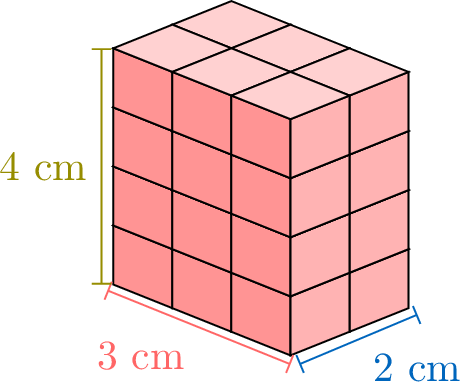
To calculate the volume of a rectangular cuboid, we can count the cubes inside, but that takes a long time. Let’s look at how the volume changes when we make the box taller, one step at a time, to find an easier way. We’ll also see how counting layer by layer can help us understand the pattern.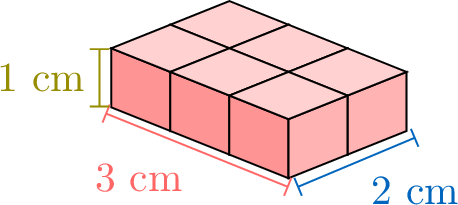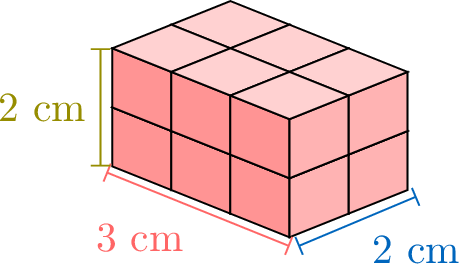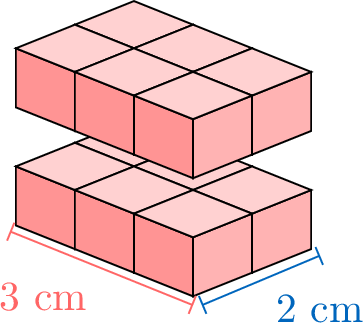
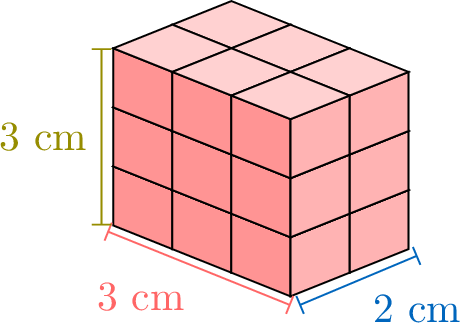\(\quad\quad\)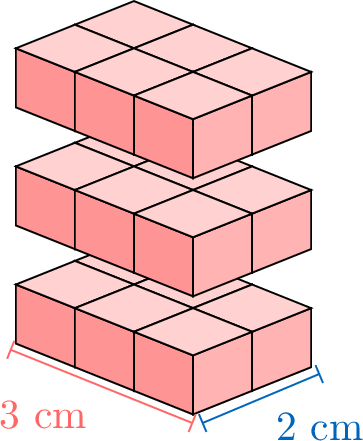
\(\quad\quad\)
\(\quad\quad\)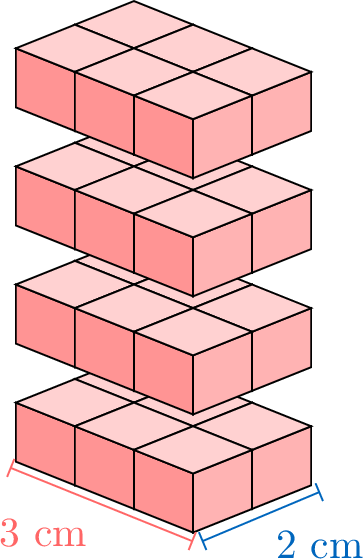
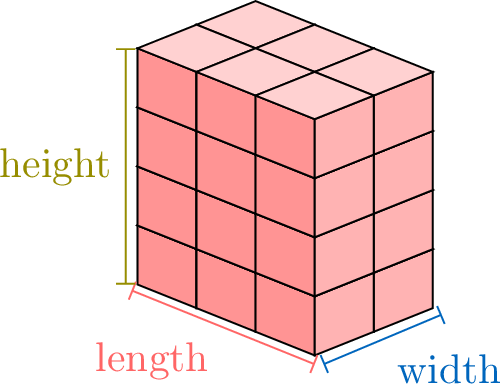
Proposition Volume of a Rectangular Cuboid
The volume of a rectangular prism is multiplying its length, width, and height:$$\text{Volume} = \textcolor{colordef}{\text{length}} \times \textcolor{colorprop}{\text{width}} \times \textcolor{olive}{\text{height}}$$
Example
Find the volume:
$$\begin{aligned}\text{Volume} &= \textcolor{colordef}{\text{length}} \times \textcolor{colorprop}{\text{width}} \times \textcolor{olive}{\text{height}}\\ &= 3\times 2 \times 4 \\ &= 24 \, \text{cm}^3\end{aligned}$$