Area
Definition
Definition Area
The area of a shape is the amount of space it covers on a flat surface. We measure it in square units, like square centimeters or square meters.
To find the area, imagine covering the shape with small squares, like tiles on a floor. Count how many squares fit inside the shape.
Example
Find the area of the red shape: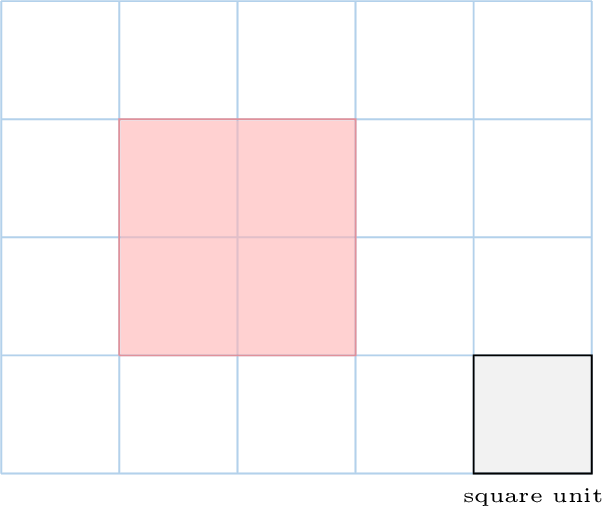

To find the area, we count the number of unit squares inside the shape.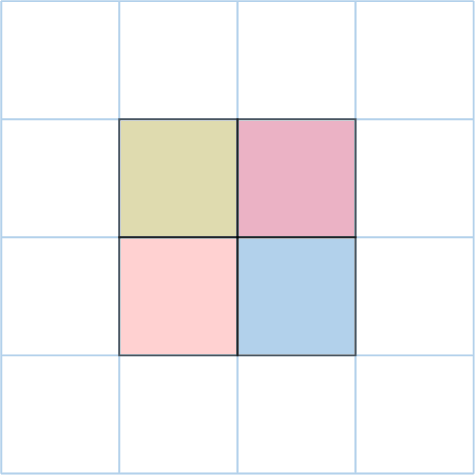
Units of Area
We can measure area using different units like tiles or paper squares. But these units are not the same for everyone. Your friend might have a bigger tile than yours, making it hard to compare. To solve this, mathematicians created universal units like the square centimeter and square meter, so everyone can measure and compare areas the same way.
Definition Units of Area
- Square Centimeter \(\left(\mathrm{cm}^2\right)\): A small unit of area, about the size of a big toe nail for a 6-year-old boy.
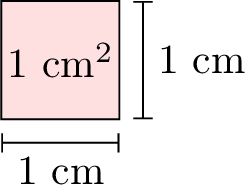
- Square Meter \(\left(\mathrm{m}^2\right)\): A larger unit of area, about the space it takes for you to lie down with your arms by your sides.
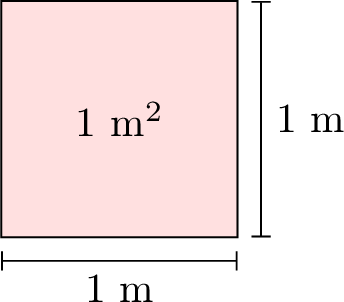
Area of Common Shapes
To find the area of the rectangle: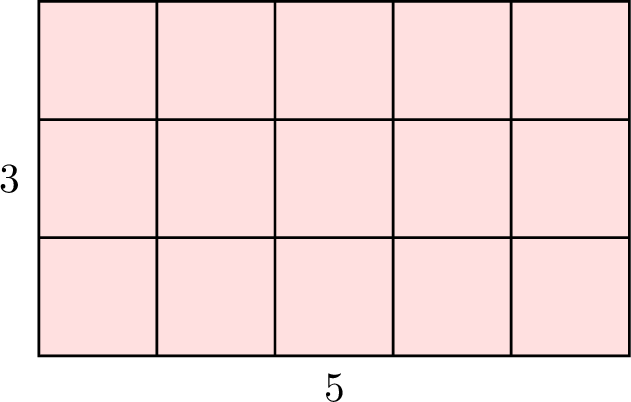

- Count the number of squares in each column:
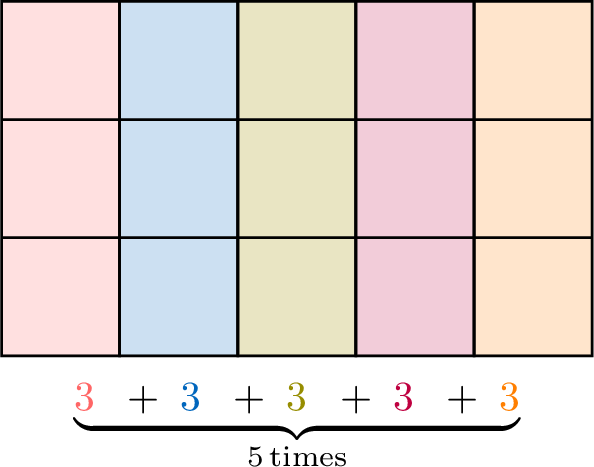
- Add them up: the area is \(\underbrace{\textcolor{colordef}{3}\;\;+\;\textcolor{colorprop}{3}\;\;+\;\textcolor{olive}{3}\;\;+\;\textcolor{purple}{3}\;\;+\;\textcolor{orange}{3}}_{5\,\text{times}} = 5 \times 3\). This shows that the area of the rectangle is found by multiplying the length by the width.
Proposition Area Formulas
| Name | Shape | Area |
| Rectangle | 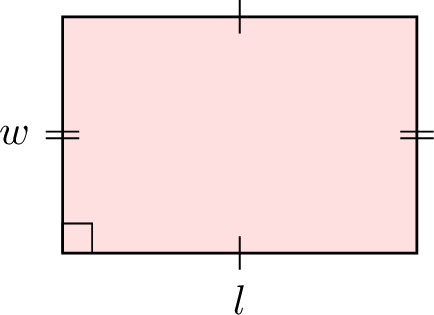 | \(l \times w\) |
| Square | 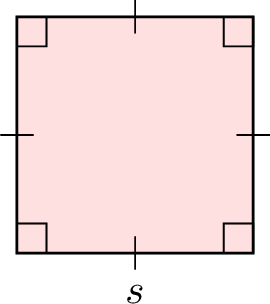 | \(s \times s\) |
Method Finding a Shape’s Area
To find the area of a rectangle or a square, multiply its length by its width.
Example
Find the area of the rectangle: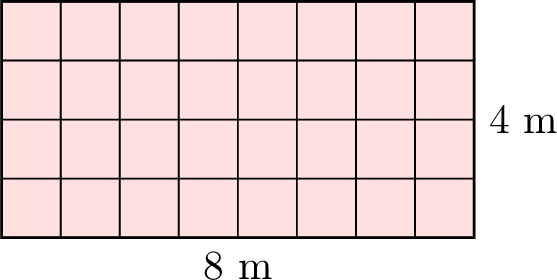

This is a rectangle with length \(L = 8\) m and width \(l = 4\) m. Using the formula for the area of a rectangle:$$\begin{aligned}[t]A &= L \times l \\&= 8 \times 4 \\&= 32 \, \mathrm{m}^2\end{aligned}$$So, the area is \(32\) square meters.