Ordering Numbers
Definitions
Comparing Numbers of Cubes
Exercise

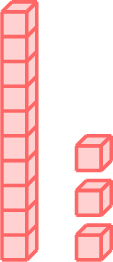
- \( \gt\) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 greater than
greater than 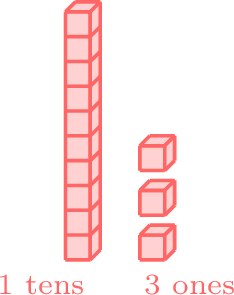
-
 \( \gt\)
\( \gt\) 
Exercise


- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 greater than
greater than 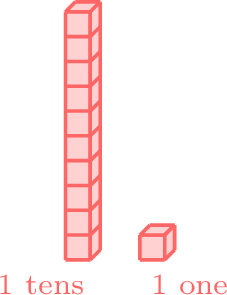
-
 \( \gt\)
\( \gt\) 
Exercise

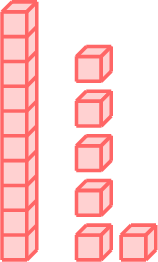
- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 less than
less than 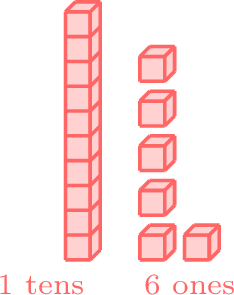
-
 \( \lt\)
\( \lt\) 
Exercise


- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
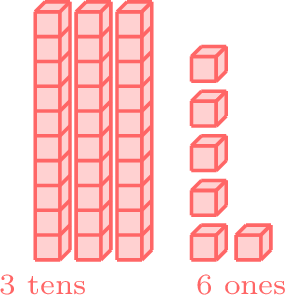 equal to
equal to 
-
 \(=\)
\(=\) 
Exercise


- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
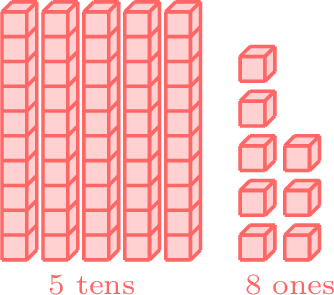 greater than
greater than 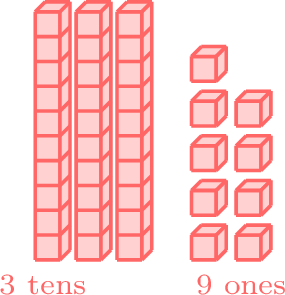
-
 \( \gt\)
\( \gt\) 
Exercise


- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 less than
less than 
-
 \( \lt\)
\( \lt\) 
Comparing Numbers of Circles
Exercise
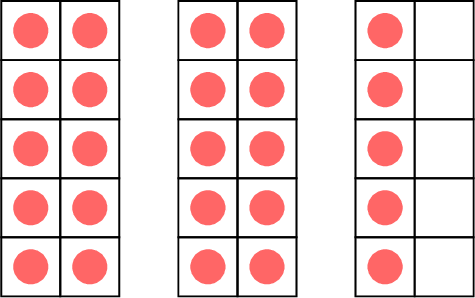
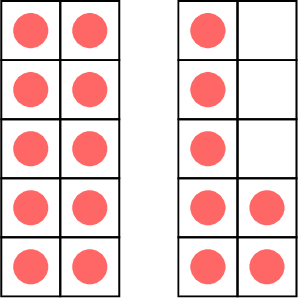
- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 greater than
greater than 
-
 \( \gt\)
\( \gt\) 
Exercise


- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 greater than
greater than 
-
 \( \gt\)
\( \gt\) 
Exercise
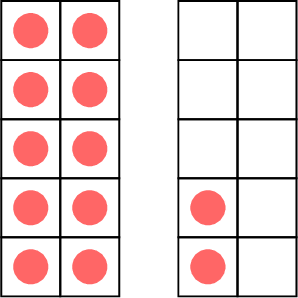
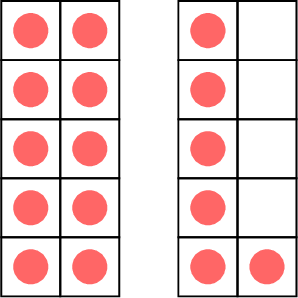
- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 less than
less than 
-
 \( \lt\)
\( \lt\) 
Exercise
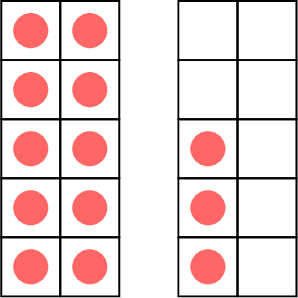
- \( \gt \) means greater than.
\( \lt \) means less than.
\(=\) means equal to. -
 less than
less than 
-
 \( \lt\)
\( \lt\) 
How to Compare 2-Digit Numbers
Comparing Numbers
Exercise
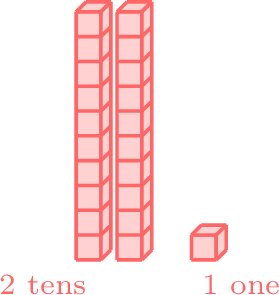
- Since 2 is in the tens place of 21 and is greater than 1 in the tens place of 13, 21 is greater than 13.
-
 greater than
greater than 
- \(21 \gt 13 \)
Exercise
- Since 3 is in the tens place of 36 and is less than 5 in the tens place of 52, 36 is less than 52.
-
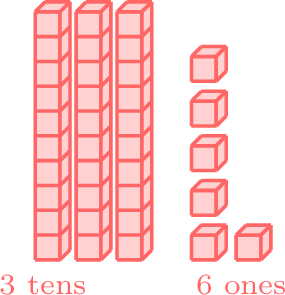 less than
less than 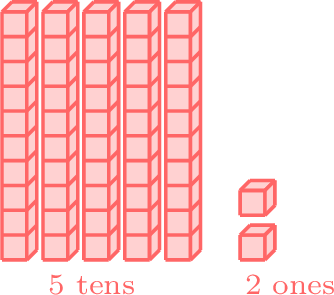
- \(36 < 52 \)
Exercise
- Since 8 is in the tens place of 88 and is greater than 2 in the tens place of 26, 88 is greater than 26.
-
 greater than
greater than 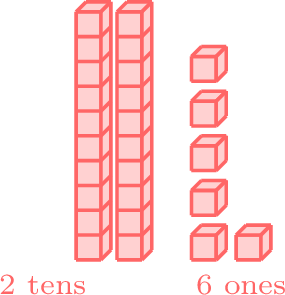
- \(88 > 26 \)
Exercise
- Since 0 is in the tens place of 05 and is less than 2 in the tens place of 22, 5 is less than 22.
-
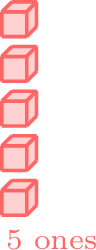 less than
less than 
- \(5 < 22 \)
Exercise
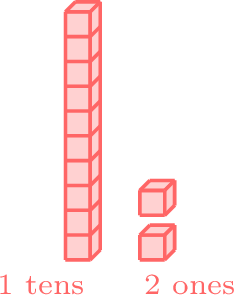
- Since 6 is in the tens place for both numbers, we compare the ones place. 8 in the ones place of 68 is greater than 2 in the ones place of 62, so 68 is greater than 62.
-
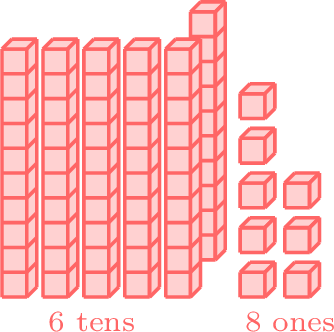 greater than
greater than 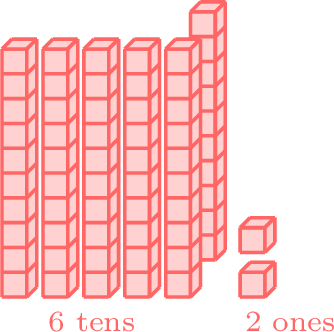
- \(68 \gt 62 \)
Exercise
- Since 9 is in the tens place of 90 and is greater than 6 in the tens place of 61, 90 is greater than 61.
-
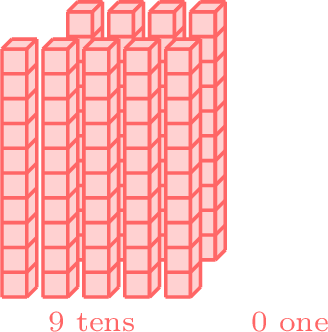 greater than
greater than 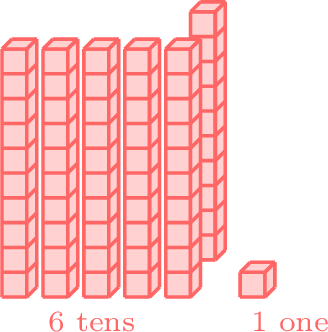
- \(90 \gt 61 \)
Exercise
- The digits in the tens place are the same (4), so we look at the ones place. Since 3 in the ones place of 43 is less than 8 in the ones place of 48, 43 is less than 48.
-
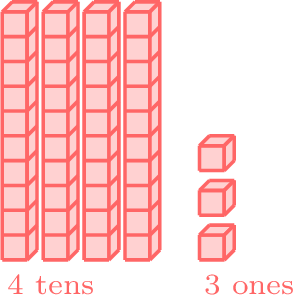 less than
less than 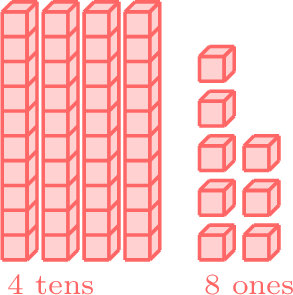
- \(43 < 48 \)
Exercise
- Since both the tens and ones places are the same in 35 and 35, the two numbers are equal.
-
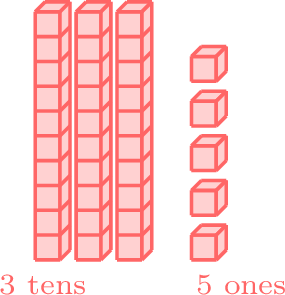 is equal to
is equal to 
- \(35 = 35\)
Ordering Numbers
Mcq
Order the following numbers from least to greatest:$$10, 6, 18, 22$$Choose one answer:
- 6 ones \( \lt\) 1 ten \( \lt\) 1 ten and 8 ones \( \lt\) 2 tens and 2 ones
- \(6\lt 10 \lt 18 \lt 22\)
Mcq
Order the following numbers from least to greatest: $$12, 5, 25, 17$$Choose one answer:
- 5 ones \( \lt\) 1 ten and 2 ones \( \lt\) 1 ten and 7 ones \( \lt\) 2 tens and 5 ones
- \(5 \lt 12 \lt 17 \lt 25\)
Mcq
Order the following numbers from least to greatest: $$15, 8, 21, 13$$Choose one answer:
- 8 ones \( \lt\) 1 ten and 3 ones \( \lt\) 1 ten and 5 ones \( \lt\) 2 tens and 1 one
- \(8 \lt 13 \lt 15 \lt 21\)
Mcq
Order the following numbers from least to greatest: $$22, 16, 30, 19$$Choose one answer:
- 1 ten and 6 ones \( \lt\) 1 ten and 9 ones \( \lt\) 2 tens and 2 ones \( \lt\) 3 tens
- \(16 \lt 19 \lt 22 \lt 30\)
Comparing Numbers in Real-World Problems
Mcq
On Monday, Lily planted 28 flowers in the garden.
On Tuesday, she planted 34 more flowers.
Which day did Lily plant more flowers?
On Tuesday, she planted 34 more flowers.
Which day did Lily plant more flowers?
- 28 = 2 tens and 8 ones.
- 34 = 3 tens and 4 ones.
- Since \(34 \gt 28\), Lily planted more flowers on Tuesday.
Mcq
On Wednesday, Farmer Joe picked up 45 eggs.
On Thursday, Farmer Joe picked up 39 eggs.
Which day did Farmer Joe pick up more eggs?
On Thursday, Farmer Joe picked up 39 eggs.
Which day did Farmer Joe pick up more eggs?
- 45 = 4 tens and 5 ones.
- 39 = 3 tens and 9 ones.
- Since \(45 \gt 39\), Farmer Joe picked up more eggs on Wednesday.
Mcq
Su has 27 marbles.
Aisha has 32 marbles.
Who has more marbles?
Aisha has 32 marbles.
Who has more marbles?
- 27 = 2 tens and 7 ones.
- 32 = 3 tens and 2 ones.
- Since \(32 \gt 27\), Aisha has more marbles than Su.
Mcq
Hugo has 53 Pokémon cards.
Louis has 47 Pokémon cards.
Who has more Pokémon cards?
Louis has 47 Pokémon cards.
Who has more Pokémon cards?
- 53 = 5 tens and 3 ones.
- 47 = 4 tens and 7 ones.
- Since \(53 \gt 47\), Hugo has more Pokémon cards than Louis.
Mcq
Maya has 73 colorful stickers.
Leo has 67 colorful stickers.
Who has more stickers?
Leo has 67 colorful stickers.
Who has more stickers?
- 73 = 7 tens and 3 ones.
- 67 = 6 tens and 7 ones.
- Since \(73 \gt 67\), Maya has more stickers than Leo.