Fractions
Definitions
Finding Fractions
Exercise
A bar represents 1. Find the fraction that represents the shaded part: 
=
= - A bar (1) is divided into \(\textcolor{colorprop}{4}\) equal parts:
- \(\textcolor{colordef}{5}\) parts are shaded.
- So, \(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{4}}\) =
Exercise
A bar represents 1. Find the fraction that represents the shaded part: 
=
= - A bar (1) is divided into \(\textcolor{colorprop}{3}\) equal parts:
- \(\textcolor{colordef}{5}\) parts are shaded.
- So, \(\dfrac{\textcolor{colordef}{5}}{\textcolor{colorprop}{3}}\) =
Exercise
A bar represents 1. Find the fraction that represents the shaded part: 
=
= - A bar (1) is divided into \(\textcolor{colorprop}{3}\) equal parts:
- \(\textcolor{colordef}{8}\) parts are shaded.
- So, \(\dfrac{\textcolor{colordef}{8}}{\textcolor{colorprop}{3}}\) =
Exercise
A circle represents 1. Find the fraction that represents the shaded part:
=
= - A circle (1) is divided into \(\textcolor{colorprop}{4}\) equal parts.
- \(\textcolor{colordef}{7}\) parts are shaded.
- So, \(\dfrac{\textcolor{colordef}{7}}{\textcolor{colorprop}{4}}\) =
Exercise
A circle represents 1. Find the fraction that represents the shaded part:
=
= - A circle (1) is divided into \(\textcolor{colorprop}{3}\) equal parts.
- \(\textcolor{colordef}{7}\) parts are shaded.
- So, \(\dfrac{\textcolor{colordef}{7}}{\textcolor{colorprop}{3}}\) =
Finding Fractions in Word Problems
Exercise
Hugo eats 3 parts of a cake that is divided into 4 equal parts. What fraction of the cake does Hugo eat? of the cake
- Hugo eats 3 of the 4 equal parts.
- So, Hugo eats \(\dfrac{3}{4}\) of the cake.
Exercise
Liam reads 5 chapters of a book that has 8 chapters. What fraction of the book does Liam read? of the book
- Liam reads 5 out of the 8 chapters.
- So, Liam reads \(\dfrac{5}{8}\) of the book.
Exercise
Vanessa paints 5 squares on a window that has 6 equal squares. What fraction of the window did she paint? of the window
- Vanessa paints 5 out of the 6 equal parts.
- So, Vanessa paints \(\dfrac{5}{6}\) of the window.
Exercise
Sophia cuts her loaf of bread into 8 equal slices. She uses 2 slices to make sandwiches. What fraction of the bread did Sophia use to make the sandwiches? of the bread
- Sophia used 2 out of the 8 equal slices of bread.
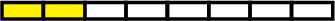
- So, Sophia used \(\dfrac{2}{8}\) of the bread to make sandwiches.
Writing Fractions from Words
Exercise
Write as fraction:one over four=
- one over four = \(\dfrac{1}{4}=\)
Exercise
Write as fraction:three over five =
- three over five = \(\dfrac{3}{5}=\)
Exercise
Write as fraction:three quarters =
- three quarters = \(\dfrac{3}{4}=\)
Exercise
Write as fraction:six over hundred =
- six over hundred (six thousandths) = \(\dfrac{6}{100}\)
On the number line
Finding Fractions With Bar Fraction Model
Exercise
Find the value of \(\textcolor{colordef}{x}\)
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 3 equals parts.
- \(\textcolor{colordef}{x}\) is located at 1 part.
- So, \(\textcolor{colordef}{x}=\dfrac{1}{3}\).
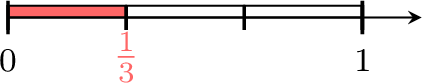
Exercise
Find the value of \(\textcolor{colordef}{x}\)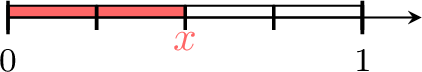
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 4 equals parts.
- \(\textcolor{colordef}{x}\) is located at 2 parts.
- So, \(\textcolor{colordef}{x}=\dfrac{2}{4}\).
Exercise
Find the value of \(\textcolor{colordef}{x}\)
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 5 equals parts.
- \(\textcolor{colordef}{x}\) is located at 3 parts.
- So, \(\textcolor{colordef}{x}=\dfrac{3}{5}\).
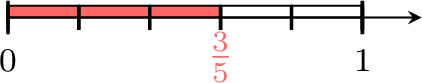
Exercise
Find the value of \(\textcolor{colordef}{x}\)
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 6 equals parts.
- \(\textcolor{colordef}{x}\) is located at 4 parts.
- So, \(\textcolor{colordef}{x}=\dfrac{4}{6}\).
Exercise
Find the value of \(\textcolor{colordef}{x}\)
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 7 equals parts.
- \(\textcolor{colordef}{x}\) is located at 3 parts.
- So, \(\textcolor{colordef}{x}=\dfrac{3}{7}\).
Finding Fractions
Exercise
Find the value of \(\textcolor{colordef}{x}\)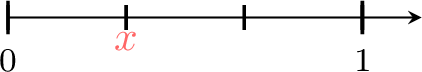
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 3 equals parts.
- \(\textcolor{colordef}{x}\) is located at 1 part from 0.
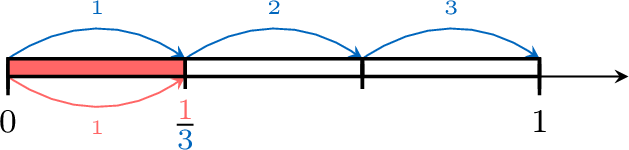
- So, \(\textcolor{colordef}{x}=\dfrac{1}{3}\).
Exercise
Find the value of \(\textcolor{colordef}{x}\)
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 4 equals parts.
- \(\textcolor{colordef}{x}\) is located at 3 parts from 0.
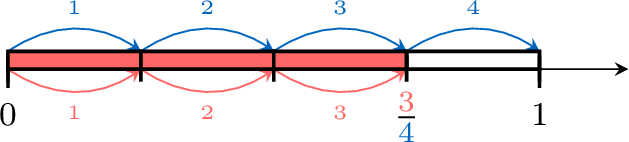
- So, \(\textcolor{colordef}{x}=\dfrac{3}{4}\).
Exercise
Find the value of \(\textcolor{colordef}{x}\)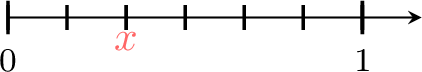
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 6 equals parts.
- \(\textcolor{colordef}{x}\) is located at 2 parts from 0.
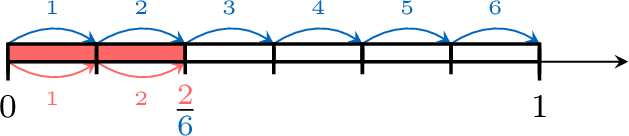
- So, \(\textcolor{colordef}{x}=\dfrac{2}{6}\).
Exercise
Find the value of \(\textcolor{colordef}{x}\)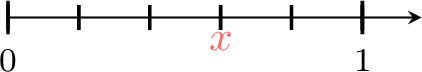
\(\textcolor{colordef}{x}=\)
\(\textcolor{colordef}{x}=\)
- 1 is divided in 5 equals parts.
- \(\textcolor{colordef}{x}\) is located at 3 parts from 0.
- So, \(\textcolor{colordef}{x}=\dfrac{3}{5}\).
Finding Fractions Greater than 1
Exercise
Find the value of \(\textcolor{olive}{x}\)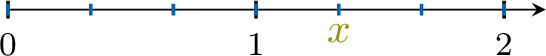
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided in \(\textcolor{colorprop}{3}\) equals parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{4}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{4}}{\textcolor{colorprop}{3}}\).
Exercise
Find the value of \(\textcolor{olive}{x}\)
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided in \(\textcolor{colorprop}{3}\) equal parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{7}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{7}}{\textcolor{colorprop}{3}}\).
Exercise
Find the value of \(\textcolor{olive}{x}\)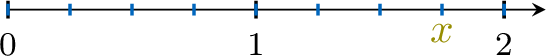
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided in \(\textcolor{colorprop}{4}\) equal parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{7}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{7}}{\textcolor{colorprop}{4}}\).
Exercise
Find the value of \(\textcolor{olive}{x}\)
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided into \(\textcolor{colorprop}{6}\) equal parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{7}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{7}}{\textcolor{colorprop}{6}}\).
Exercise
Find the value of \(\textcolor{olive}{x}\)
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided into \(\textcolor{colorprop}{5}\) equal parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{8}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{8}}{\textcolor{colorprop}{5}}\).
Exercise
Find the value of \(\textcolor{olive}{x}\)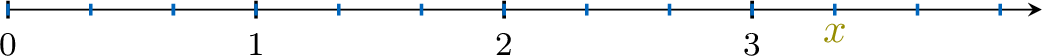
\(\textcolor{olive}{x}=\)
\(\textcolor{olive}{x}=\)
- 1 is divided into \(\textcolor{colorprop}{3}\) equal parts.
- \(\textcolor{olive}{x}\) is located at \(\textcolor{colordef}{10}\) parts from 0.
- So, \(\textcolor{olive}{x}=\dfrac{\textcolor{colordef}{10}}{\textcolor{colorprop}{3}}\).
Equivalent Fractions
Finding the Missing Numerator
Exercise
-
= 
= 
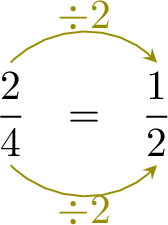- The second denominator \(2\) is the first denominator \(4\) divided by 2 : \(4 \times 2 = 2\).
- To keep the fractions equivalent, the numerator must also be divided by 2.
- This means: \(2 \div 2 = 1\), so the missing numerator is 1.
Exercise
-
= 
= 
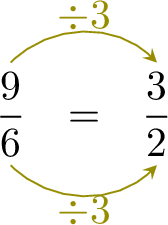- The second denominator \( 2 \) is the first denominator \( 6 \) divided by 3 : \( 6 \div 3 = 2 \).
- To keep the fractions equivalent, the numerator must also be divided by 3.
- This means: \( 9 \div 3 = 3 \), so the missing numerator is 3.
Exercise
-
= 
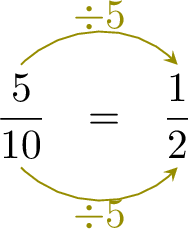= - The second denominator \( 2 \) is the first denominator \( 10 \) divided by 5 : \( 10 \div 5 = 2 \).
- To keep the fractions equivalent, the numerator must also be divided by 5.
- This means: \( 5 \div 5 = 1 \), so the missing numerator is 1.
Exercise
-
= 
= 
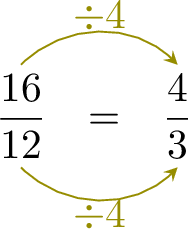- The second denominator \( 3 \) is the first denominator \( 12 \) divided by 4 : \( 12 \div 4 = 3 \).
- To keep the fractions equivalent, the numerator must also be divided by 4.
- This means: \( 16 \div 4 = 4 \), so the missing numerator is 4.
Exercise
-
= 
= 
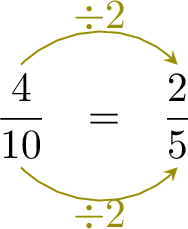- The second denominator \( 5 \) is the first denominator \( 10 \) divided by 2 : \( 10 \div 2 = 5 \).
- To keep the fractions equivalent, the numerator must also be divided by 2.
- This means: \( 4 \div 2 = 2 \), so the missing numerator is 2.
Finding the Missing Denominator
Exercise
- = =
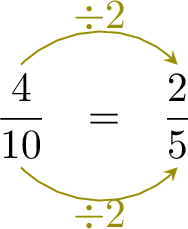- The second numerator \( 2 \) is the first numerator \( 4 \) divided by 2 : \( 4 \div 2 = 2 \).
- To keep the fractions equivalent, the denominator must also be divided by 2.
- This means: \( 10 \div 2 = 5 \), so the missing denominator is 5.
Exercise
-
= 
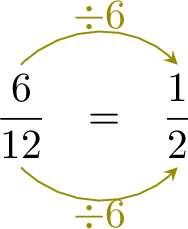= - The second numerator \( 1 \) is the first numerator \( 6 \) divided by 6 : \( 6 \div 6 = 1 \).
- To keep the fractions equivalent, the denominator must also be divided by 6.
- This means: \( 12 \div 6 = 2 \), so the missing denominator is 2.
Exercise
- = =
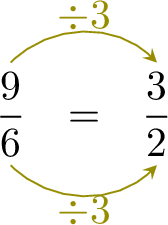- The second numerator \( 3 \) is the first numerator \( 9 \) divided by 3 : \( 9 \div 3 = 3 \).
- To keep the fractions equivalent, the denominator must also be divided by 3.
- This means: \( 6 \div 3 = 2 \), so the missing denominator is 2.
Exercise
-
= 
= 
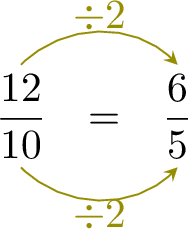- The second numerator \( 6 \) is the first numerator \( 12 \) divided by 2 : \( 12 \div 2 = 6 \).
- To keep the fractions equivalent, the denominator must also be divided by 2.
- This means: \( 10 \div 2 = 5 \), so the missing denominator is 5.
Simplification
Simplifying Fractions
Exercise
Simplify: \(\dfrac{4}{6}=\)
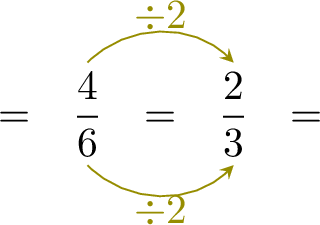
Exercise
Simplify: \(\dfrac{2}{4}=\)
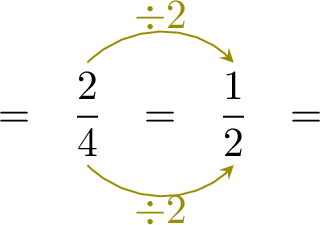
Exercise
Simplify: \(\dfrac{10}{8}=\)
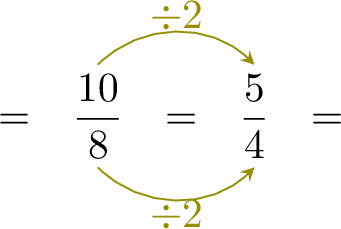
Exercise
Simplify: \(\dfrac{6}{9}=\)
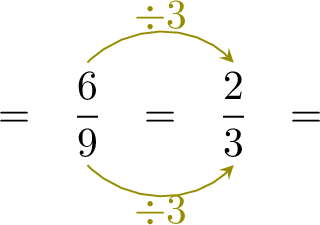
Ordering Fractions
Comparing with Same Denominator with Bar Models
Exercise
Compare using \(\gt,\lt,=\):
\(=\dfrac{1}{4}\) \(\dfrac{2}{4}=\) 
\(=\dfrac{1}{4}\) \(\dfrac{2}{4}=\) - \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{1}{4}\) less than \(\dfrac{2}{4}=\)
- \(=\dfrac{1}{4}\lt \dfrac{2}{4}=\)
Exercise
Compare using \(\gt,\lt,=\):
\(=\dfrac{3}{5}\) \(\dfrac{2}{5}=\) 
\(=\dfrac{3}{5}\) \(\dfrac{2}{5}=\) - \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{3}{5}\) greater than \(\dfrac{2}{5}=\)
- \(=\dfrac{3}{5}\gt \dfrac{2}{5}=\)
Exercise
Compare using \(\gt,\lt,=\):
\(=\dfrac{4}{7}\) \(\dfrac{3}{7}=\) 
\(=\dfrac{4}{7}\) \(\dfrac{3}{7}=\) - \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{4}{7}\) greater than \(\dfrac{3}{7}=\)
- \(=\dfrac{4}{7}\gt \dfrac{3}{7}=\)
Exercise
Compare using \(\gt,\lt,=\):
\(=\dfrac{7}{4}\) \(\dfrac{5}{4}=\) 
\(=\dfrac{7}{4}\) \(\dfrac{5}{4}=\) - \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{7}{4}\) greater than \(\dfrac{5}{4}=\)
- \(=\dfrac{7}{4}\gt \dfrac{5}{4}=\)
Exercise
Compare using \(\gt,\lt,=\):
\(\dfrac{5}{3}\) \(\dfrac{6}{3}=\) 
\(\dfrac{5}{3}\) \(\dfrac{6}{3}=\) - \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{5}{3}\) less than \(\dfrac{6}{3}=\)
- \(=\dfrac{5}{3}\lt \dfrac{6}{3}=\)
Comparing With Same Denominator
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{7}{3}\) \(\dfrac{6}{3}\)
- \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. -
\(=\dfrac{7}{3}\) less than \(\dfrac{6}{3}=\) - So \(\dfrac{7}{3}\gt\dfrac{6}{3}\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{5}{4}\) \(\dfrac{3}{4}\)
- \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. - \(=\dfrac{5}{4}\) greater than \(\dfrac{3}{4}=\)
- So \(\dfrac{5}{4}\gt\dfrac{3}{4}\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{2}{6}\) \(\dfrac{4}{6}\)
- \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. -
\(=\dfrac{2}{6}\) less than \(\dfrac{4}{6}=\) 
- So \(\dfrac{2}{6}\lt\dfrac{4}{6}\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{7}{5}\) \(\dfrac{3}{5}\)
- \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. -
\(=\dfrac{7}{5}\) greater than \(\dfrac{3}{5}=\) - So \(\dfrac{7}{5}\gt\dfrac{3}{5}\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{3}{8}\) \(\dfrac{6}{8}\)
- \(\gt\) means greater than.
\(\lt\) means less than.
\(=\) means equal to. -
\(=\dfrac{3}{8}\) less than \(\dfrac{6}{8}=\) 
- So \(\dfrac{3}{8}\lt\dfrac{6}{8}\)
Comparing Fractions with Different Denominators
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{3}{4}\) \(\dfrac{1}{2}\) Hint: color the bars below to help you compare the fractions.\(\dfrac{3}{4}=\) 
and \(\dfrac{1}{2}\)=
and \(\dfrac{1}{2}\)=- Find equivalent fractions with the same denominator:
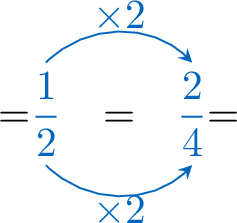
- Compare with same denominator: \(=\textcolor{colordef}{\dfrac{3}{4}} \gt \dfrac{\textcolor{colorprop}{2}}{\textcolor{colorprop}{4}}=\)
- So \(=\textcolor{colordef}{\dfrac{3}{4}} \gt \textcolor{colorprop}{\dfrac{1}{2}}=\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{5}{6}\) \(\dfrac{2}{3}\) Hint: color the bars below to help you compare the fractions.\(\dfrac{5}{6}=\) 
and \(\dfrac{2}{3}\)=
and \(\dfrac{2}{3}\)=- Find equivalent fractions with the same denominator:
- Compare with same denominator:
\(=\textcolor{colordef}{\dfrac{5}{6}} \gt \dfrac{\textcolor{colorprop}{4}}{\textcolor{colorprop}{6}}=\) 
- So \(=\textcolor{colordef}{\dfrac{5}{6}} \gt \textcolor{colorprop}{\dfrac{2}{3}}=\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{5}{6}\) \(\dfrac{1}{2}\) Hint: color the bars below to help you compare the fractions.\(\dfrac{5}{6}=\) and \(\dfrac{1}{2}\)=
and \(\dfrac{1}{2}\)=- Find equivalent fractions with the same denominator:
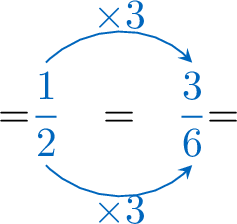
- Compare with same denominator: \(=\textcolor{colordef}{\dfrac{5}{6}} \gt \dfrac{\textcolor{colorprop}{3}}{\textcolor{colorprop}{6}}=\)
- So \(=\textcolor{colordef}{\dfrac{5}{6}} \gt \textcolor{colorprop}{\dfrac{1}{2}}=\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{7}{6}\) \(\dfrac{4}{3}\) Hint: color the bars below to help you compare the fractions.\(\dfrac{7}{6}=\) 
and \(\dfrac{4}{3}\)=
and \(\dfrac{4}{3}\)=- Find equivalent fractions with the same denominator:
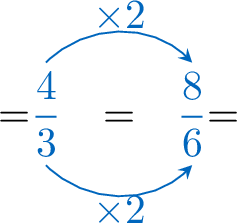
- Compare with same denominator:
\(=\textcolor{colordef}{\dfrac{7}{6}} \lt \dfrac{\textcolor{colorprop}{8}}{\textcolor{colorprop}{6}}=\) 
- So \(=\textcolor{colordef}{\dfrac{7}{6}} \lt \textcolor{colorprop}{\dfrac{4}{3}}=\)
Exercise
Compare using \(\gt,\lt,=\):\(\dfrac{3}{4}\) \(\dfrac{7}{8}\) Hint: color the bars below to help you compare the fractions.\(\dfrac{3}{4}=\) and \(\dfrac{7}{8}\)=
and \(\dfrac{7}{8}\)=- Find equivalent fractions with the same denominator:
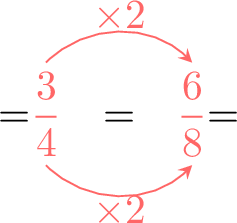
- Compare with same denominator: \(=\textcolor{colordef}{\dfrac{6}{8}} \lt \dfrac{\textcolor{colorprop}{7}}{\textcolor{colorprop}{8}}=\)
- So \(=\textcolor{colordef}{\dfrac{3}{4}} \lt \textcolor{colorprop}{\dfrac{7}{8}}=\)
Comparing Fractions to Real-World Problems
Mcq
Hugo spends \(\frac{3}{8}\) of his money on Pokemon cards and \(\frac{1}{4}\) of his money to buy a tennis racket. On which does he spend more money?
- Convert to a common denominator:
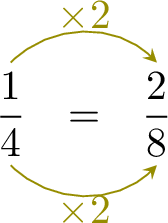
- Since \(\dfrac{2}{8} \lt \dfrac{3}{8}\), \(\dfrac{1}{4}\lt\dfrac{3}{8}\)
- So, Hugo spends more money on Pokemon cards than on a tennis racquet.
Mcq
Sophie spends \(\frac{1}{2}\) of her money on clothes and \(\frac{3}{8}\) of her money on books. On which does she spend more money?
- Convert to a common denominator:
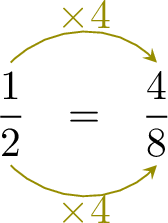
- Since \(\dfrac{4}{8} \gt \dfrac{3}{8}\), \(\dfrac{1}{2}\gt\dfrac{3}{8}\)
- So, Sophie spends more money on clothes than on books.
Mcq
For her cake recipe, Sarah uses \(\frac{2}{5}\) of a cup of butter and \(\frac{3}{10}\) of a cup of sugar. Which ingredient does she use more of?
- Convert to a common denominator:
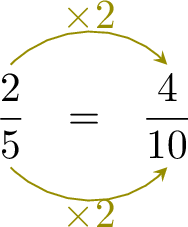
- Since \(\dfrac{4}{10} \gt \dfrac{3}{10}\), Sarah uses more butter than sugar.
Mcq
In Class A, \(\frac{6}{10}\) of the students are girls, and in Class B, \(\frac{13}{20}\) of the students are girls. In which class is the proportion of girls higher?
- Convert to a common denominator:
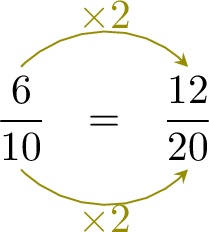
- Since \(\dfrac{12}{20} \lt \dfrac{13}{20}\), the proportion of girls is higher in Class B.
Addition and Subtraction with Common Denominators
Adding Fractions with Common Denominators
Exercise
\(+\) 
\(=\)\(\dfrac{1}{4} + \dfrac{2}{4} =\)
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{1}{4} + \dfrac{2}{4} &= \dfrac{1 + 2}{4} \\&= \dfrac{3}{4}\end{aligned}\)
Exercise
\(+\) 
\(=\)\(\dfrac{3}{5} + \dfrac{1}{5} =\)
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{5} + \dfrac{1}{5} &= \dfrac{3 + 1}{5} \\&= \dfrac{4}{5}\end{aligned}\)
Exercise
\(+\) 
\(=\)\(\dfrac{2}{6} + \dfrac{3}{6} =\)
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{2}{6} + \dfrac{3}{6} &= \dfrac{2 + 3}{6} \\&= \dfrac{5}{6}\end{aligned}\)
Exercise
\(+\) 
\(=\)\(\dfrac{2}{3} + \dfrac{2}{3} =\)
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{2}{3} + \dfrac{2}{3} &= \dfrac{2 + 2}{3} \\&= \dfrac{4}{3}\end{aligned}\)
Exercise
\(+\) 
\(=\)\(\dfrac{4}{5} + \dfrac{2}{5} =\)
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{4}{5} + \dfrac{2}{5} &= \dfrac{4 + 2}{5} \\&= \dfrac{6}{5}\end{aligned}\)
Adding Fractions with Common Denominators
Exercise
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{1}{4} + \dfrac{2}{4} &= \dfrac{1 + 2}{4} \\&= \dfrac{3}{4}\end{aligned}\)
Exercise
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{5} + \dfrac{1}{5} &= \dfrac{3 + 1}{5} \\&= \dfrac{4}{5}\end{aligned}\)
Exercise
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{2}{6} + \dfrac{3}{6} &= \dfrac{2 + 3}{6} \\&= \dfrac{5}{6}\end{aligned}\)
Exercise
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{2}{3} + \dfrac{2}{3} &= \dfrac{2 + 2}{3} \\&= \dfrac{4}{3}\end{aligned}\)
Exercise
- \(+\) \(=\)
- \(\begin{aligned}[t]\dfrac{4}{5} + \dfrac{2}{5} &= \dfrac{4 + 2}{5} \\&= \dfrac{6}{5}\end{aligned}\)
Subtracting Fractions with Common Denominators
Exercise
\(-\) 
\(=\)\(\dfrac{3}{4} - \dfrac{2}{4} =\)
- \(-\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{4} - \dfrac{2}{4} &= \dfrac{3 - 2}{4} \\&= \dfrac{1}{4}\end{aligned}\)
Exercise
\(-\) \(=\)\(\dfrac{4}{5} - \dfrac{3}{5} =\)
- \(-\) \(=\)
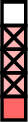
- \(\begin{aligned}[t]\dfrac{4}{5} - \dfrac{3}{5} &= \dfrac{4 - 3}{5} \\&= \dfrac{1}{5}\end{aligned}\)
Exercise
\(-\) \(=\)\(\dfrac{3}{4} - \dfrac{1}{4} =\)
- \(-\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{4} - \dfrac{1}{4} &= \dfrac{3 -1}{4} \\&= \dfrac{2}{4}\end{aligned}\)
Exercise
\(-\) \(=\)\(\dfrac{4}{3} - \dfrac{2}{3} =\)
- \(-\) \(=\)
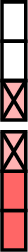
- \(\begin{aligned}[t]\dfrac{4}{3} - \dfrac{2}{3} &= \dfrac{4 - 2}{3} \\&= \dfrac{2}{3}\end{aligned}\)
Exercise
\(-\) \(=\)\(\dfrac{7}{6} - \dfrac{2}{6} =\)
- \(-\) \(=\)
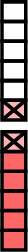
- \(\begin{aligned}[t]\dfrac{7}{6} - \dfrac{2}{6} &= \dfrac{7 - 2}{6} \\&= \dfrac{5}{6}\end{aligned}\)
Subtracting Fractions with Common Denominators
Exercise
- \(-\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{4} - \dfrac{2}{4} &= \dfrac{3 - 2}{4} \\&= \dfrac{1}{4}\end{aligned}\)
Exercise
- \(-\) \(=\)
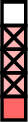
- \(\begin{aligned}[t]\dfrac{4}{5} - \dfrac{3}{5} &= \dfrac{4 - 3}{5} \\&= \dfrac{1}{5}\end{aligned}\)
Exercise
- \(-\) \(=\)
- \(\begin{aligned}[t]\dfrac{3}{4} - \dfrac{1}{4} &= \dfrac{3 -1}{4} \\&= \dfrac{2}{4}\end{aligned}\)
Exercise
- \(-\) \(=\)
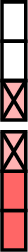
- \(\begin{aligned}[t]\dfrac{4}{3} - \dfrac{2}{3} &= \dfrac{4 - 2}{3} \\&= \dfrac{2}{3}\end{aligned}\)
Exercise
- \(-\) \(=\)
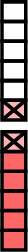
- \(\begin{aligned}[t]\dfrac{7}{6} - \dfrac{2}{6} &= \dfrac{7 - 2}{6} \\&= \dfrac{5}{6}\end{aligned}\)
Addition and Subtraction with Different Denominators
Finding a Common Denominator
Exercise
- Since \( \dfrac{1}{2}\) and \( \dfrac{1}{4} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 4 \):
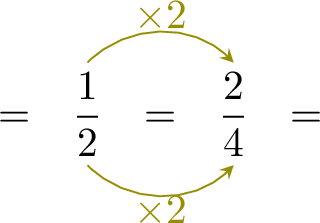
- $$\begin{aligned}[t]\dfrac{1}{2}+\dfrac{1}{4} &= \dfrac{2}{4} + \dfrac{1}{4}\\\end{aligned}$$
\(+\) 
\(=\) 
\(+\)
Exercise
- Since \( \dfrac{2}{3} \) and \( \dfrac{5}{6} \) have different denominators, rewrite \( \dfrac{2}{3} \) with the denominator \( 6 \):
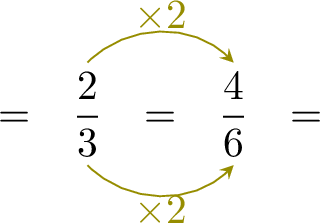
- $$\begin{aligned}[t]\dfrac{2}{3}+\dfrac{5}{6} &= \dfrac{4}{6} + \dfrac{5}{6}\\\end{aligned}$$
\(+\) 
\(=\) 
\(+\)
Exercise
- Since \( \dfrac{3}{8} \) and \( \dfrac{1}{2} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 8 \):
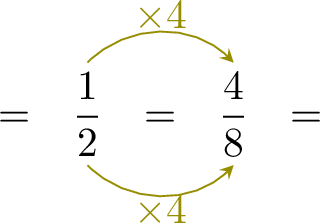
- $$\begin{aligned}[t]\dfrac{3}{8}+\dfrac{1}{2} &= \dfrac{3}{8} + \dfrac{4}{8}\\\end{aligned}$$
\(+\) 
\(=\) \(+\) 
Exercise
- Since \( \dfrac{5}{6} \) and \( \dfrac{3}{2} \) have different denominators, rewrite \( \dfrac{3}{2} \) with the denominator \( 6 \):
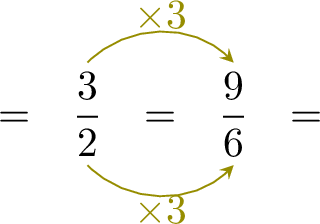
- $$\begin{aligned}[t]\dfrac{5}{6}+\dfrac{3}{2} &= \dfrac{5}{6} + \dfrac{9}{6}\\\end{aligned}$$
\(+\) 
\(=\) \(+\) 
Exercise
- Since \( \dfrac{3}{10} \) and \( \dfrac{6}{5} \) have different denominators, rewrite \( \dfrac{6}{5} \) with the denominator \( 10 \):
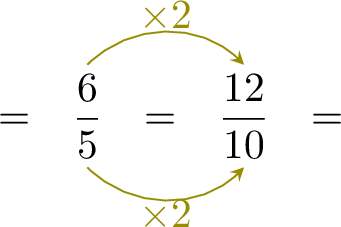
- $$\begin{aligned}[t]\dfrac{3}{10}+\dfrac{6}{5} &= \dfrac{3}{10} + \dfrac{12}{10}\\\end{aligned}$$
\(+\) 
\(=\) \(+\) 
Adding Fractions Step by Step
Exercise
| \(\dfrac{1}{2}+\dfrac{1}{4}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{1}{2}\) and \( \dfrac{1}{4} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 4 \):
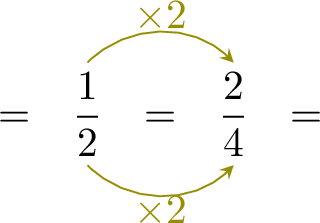
- $$\begin{aligned}[t]\dfrac{1}{2}+\dfrac{1}{4} &= \dfrac{2}{4} + \dfrac{1}{4}\\&= \dfrac{3}{4}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\) 
Exercise
| \(\dfrac{1}{3}+\dfrac{5}{6}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{1}{3}\) and \( \dfrac{5}{6} \) have different denominators, rewrite \( \dfrac{1}{3} \) with the denominator \( 6 \):
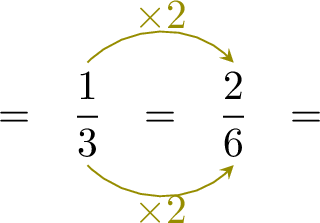
- $$\begin{aligned}[t]\dfrac{1}{3}+\dfrac{5}{6} &= \dfrac{2}{6} + \dfrac{5}{6}\\&= \dfrac{7}{6}\\\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
| \(\dfrac{1}{2}+\dfrac{2}{6}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{1}{2}\) and \( \dfrac{2}{6} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 6 \):
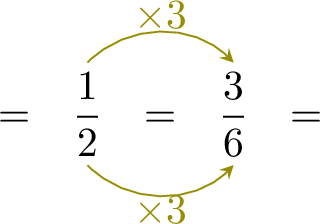
- $$\begin{aligned}[t]\dfrac{1}{2}+\dfrac{2}{6} &= \dfrac{3}{6} + \dfrac{2}{6}\\&= \dfrac{5}{6}\end{aligned}$$
- \(+\)
\(=\) 
\(+\) \(=\) 
Exercise
| \(\dfrac{3}{10}+\dfrac{2}{5}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{3}{10}\) and \( \dfrac{2}{5} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
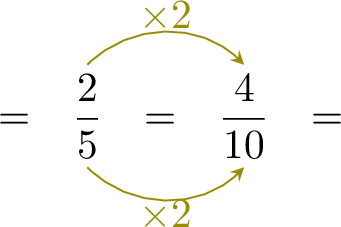
- $$\begin{aligned}[t]\dfrac{3}{10}+\dfrac{2}{5} &= \dfrac{3}{10} + \dfrac{4}{10}\\&= \dfrac{7}{10}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) 
\(=\) 
Exercise
| \(\dfrac{3}{8}+\dfrac{1}{2}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{3}{8}\) and \( \dfrac{1}{2} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 8 \):
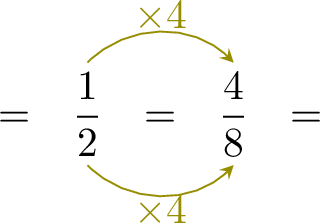
- $$\begin{aligned}[t]\dfrac{3}{8}+\dfrac{1}{2} &= \dfrac{3}{8} + \dfrac{4}{8}\\&= \dfrac{7}{8}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) 
\(=\) 
Adding Fractions
Exercise
| \(\dfrac{2}{5}+\dfrac{3}{10}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{2}{5}\) and \( \dfrac{3}{10} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
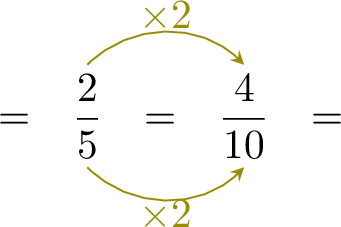
- $$\begin{aligned}[t]\dfrac{2}{5}+\dfrac{3}{10} &= \dfrac{4}{10} + \dfrac{3}{10}\\&= \dfrac{7}{10}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
| \(\dfrac{3}{4}+\dfrac{1}{8}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{3}{4}\) and \( \dfrac{1}{8} \) have different denominators, rewrite \( \dfrac{3}{4} \) with the denominator \( 8 \):
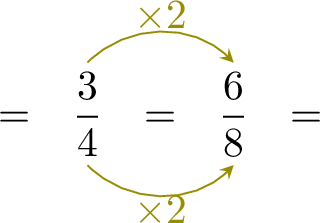
- $$\begin{aligned}[t]\dfrac{3}{4}+\dfrac{1}{8} &= \dfrac{6}{8} + \dfrac{1}{8}\\&= \dfrac{7}{8}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
| \(\dfrac{1}{2}+\dfrac{2}{6}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{1}{2}\) and \( \dfrac{2}{6} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 6 \):
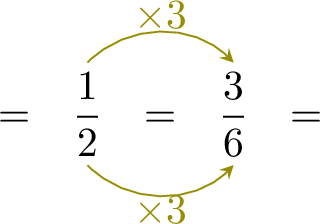
- $$\begin{aligned}[t]\dfrac{1}{2}+\dfrac{2}{6} &= \dfrac{3}{6} + \dfrac{2}{6}\\&= \dfrac{5}{6}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\)
Exercise
| \(\dfrac{3}{10}+\dfrac{2}{5}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{3}{10}\) and \( \dfrac{2}{5} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
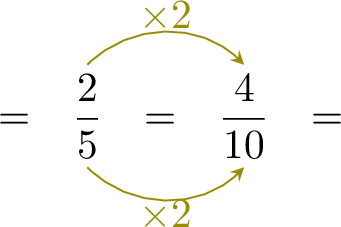
- $$\begin{aligned}[t]\dfrac{3}{10}+\dfrac{2}{5} &= \dfrac{3}{10} + \dfrac{4}{10}\\&= \dfrac{7}{10}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\)
Exercise
| \(\dfrac{3}{8}+\dfrac{1}{2}\) | \(=\) | \(+\) |
| \(=\) |
- Since \( \dfrac{3}{8}\) and \( \dfrac{1}{2} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 8 \):
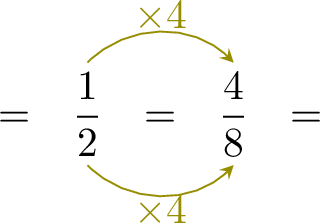
- $$\begin{aligned}[t]\dfrac{3}{8}+\dfrac{1}{2} &= \dfrac{3}{8} + \dfrac{4}{8}\\&= \dfrac{7}{8}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\)
Adding Fractions
Exercise
- Since \( \dfrac{2}{5}\) and \( \dfrac{3}{10} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
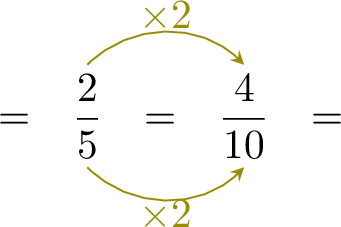
- $$\begin{aligned}[t]\dfrac{2}{5}+\dfrac{3}{10} &= \dfrac{4}{10} + \dfrac{3}{10}\\&= \dfrac{7}{10}\end{aligned}$$
- \(+\)
\(=\) 
\(+\) \(=\)
Exercise
- Since \( \dfrac{1}{4}\) and \( \dfrac{3}{8} \) have different denominators, rewrite \( \dfrac{1}{4} \) with the denominator \( 8 \):
- $$\begin{aligned}[t]\dfrac{1}{4}+\dfrac{3}{8} &= \dfrac{2}{8} + \dfrac{3}{8}\\&= \dfrac{5}{8}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
- Since \( \dfrac{2}{3}\) and \( \dfrac{1}{6} \) have different denominators, rewrite \( \dfrac{2}{3} \) with the denominator \( 6 \):
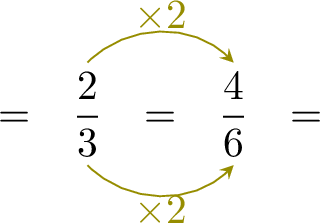
- $$\begin{aligned}[t]\dfrac{2}{3}+\dfrac{1}{6} &= \dfrac{4}{6} + \dfrac{1}{6}\\&= \dfrac{5}{6}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
- Since \( \dfrac{3}{5}\) and \( \dfrac{2}{15} \) have different denominators, rewrite \( \dfrac{3}{5} \) with the denominator \( 15 \):
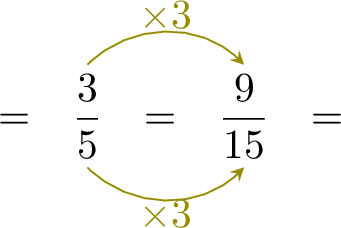
- $$\begin{aligned}[t]\dfrac{3}{5}+\dfrac{2}{15} &= \dfrac{9}{15} + \dfrac{2}{15}\\&= \dfrac{11}{15}\end{aligned}$$
\(+\) 
\(=\) 
\(+\) \(=\) 
Exercise
- Since \( \dfrac{3}{10}\) and \( \dfrac{2}{5} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
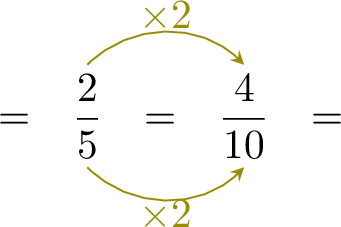
- $$\begin{aligned}[t]\dfrac{3}{10}+\dfrac{2}{5} &= \dfrac{3}{10} + \dfrac{4}{10}\\&= \dfrac{7}{10}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\)
Exercise
- Since \( \dfrac{3}{8}\) and \( \dfrac{1}{2} \) have different denominators, rewrite \( \dfrac{1}{2} \) with the denominator \( 8 \):
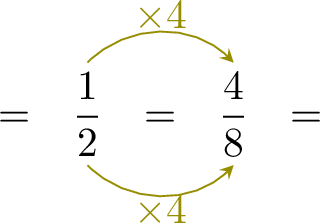
- $$\begin{aligned}[t]\dfrac{3}{8}+\dfrac{1}{2} &= \dfrac{3}{8} + \dfrac{4}{8}\\&= \dfrac{7}{8}\end{aligned}$$
- \(+\)
\(=\) \(+\) \(=\)
Subtracting Fractions
Exercise
| \(\dfrac{2}{5}-\dfrac{3}{10}\) | \(=\) | \(-\) |
| \(=\) |
- Since \( \dfrac{2}{5}\) and \( \dfrac{3}{10} \) have different denominators, rewrite \( \dfrac{2}{5} \) with the denominator \( 10 \):
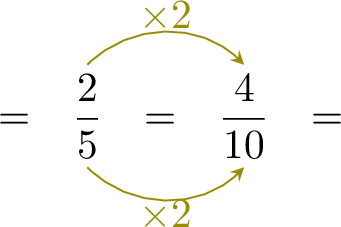
- $$\begin{aligned}[t]\dfrac{2}{5}-\dfrac{3}{10} &= \dfrac{4}{10} - \dfrac{3}{10}\\&= \dfrac{4-3}{10} \\&= \dfrac{1}{10}\end{aligned}$$
- \(-\)
\(=\) \(-\) \(=\) 
Exercise
| \(\dfrac{7}{6}-\dfrac{1}{3}\) | \(=\) | \(-\) |
| \(=\) |
- Since \( \dfrac{7}{6} \) and \( \dfrac{1}{3} \) have different denominators, rewrite \( \dfrac{1}{3} \) with the denominator \( 6 \):
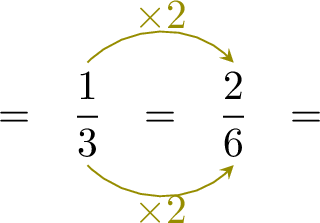
- $$\begin{aligned}[t]\dfrac{7}{6}-\dfrac{1}{3} &= \dfrac{7}{6} - \dfrac{2}{6}\\&= \dfrac{7-2}{6} \\&= \dfrac{5}{6}\end{aligned}$$
\(-\) 
\(=\) \(-\) 
\(=\) 
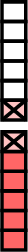
Exercise
| \(\dfrac{7}{8}-\dfrac{3}{4}\) | \(=\) | \(-\) |
| \(=\) |
- Since \( \dfrac{7}{8} \) and \( \dfrac{3}{4} \) have different denominators, rewrite \( \dfrac{3}{4} \) with the denominator \( 8 \):
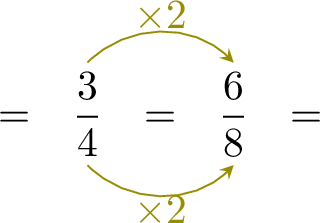
- $$\begin{aligned}[t]\dfrac{7}{8}-\dfrac{3}{4} &= \dfrac{7}{8} - \dfrac{6}{8}\\&= \dfrac{7-6}{8} \\&= \dfrac{1}{8}\end{aligned}$$
\(-\) 
\(=\) \(-\) 
\(=\) 
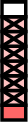
Exercise
| \(\dfrac{5}{3} - \dfrac{5}{9}\) | \(=\) | \(-\) |
| \(=\) |
- Since \( \dfrac{5}{3} \) and \( \dfrac{5}{9} \) have different denominators, rewrite \( \dfrac{5}{3} \) with the denominator \( 9 \):
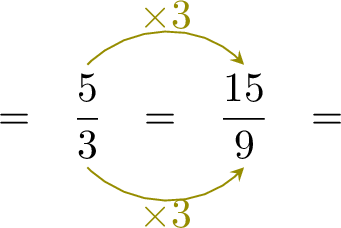
- $$\begin{aligned}[t]\dfrac{5}{3} - \dfrac{5}{9} &= \dfrac{15}{9} - \dfrac{5}{9}\\&= \dfrac{15 - 5}{9} \\&= \dfrac{10}{9}\end{aligned}$$
\(-\) 
\(=\) 
\(-\) \(=\) 
Exercise
| \(\dfrac{7}{2} - \dfrac{7}{4}\) | \(=\) | \(-\) |
| \(=\) |
- Since \( \dfrac{7}{2} \) and \( \dfrac{7}{4} \) have different denominators, rewrite \( \dfrac{7}{2} \) with the denominator \( 4 \):
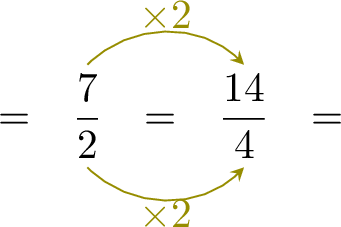
- $$\begin{aligned}[t]\dfrac{7}{2} - \dfrac{7}{4} &= \dfrac{14}{4} - \dfrac{7}{4}\\&= \dfrac{14 - 7}{4} \\&= \dfrac{7}{4}\end{aligned}$$
\(-\) 
\(=\) 
\(-\) \(=\) 
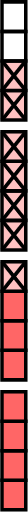
Solving Real-World Problems
Exercise
Louis has a whole cake. He cuts it into 8 equal slices and eats 3 slices. What fraction of the whole cake remains? of the cake
- Represent the cake as a fraction
The whole cake is divided into 8 slices, so the whole cake is \( \dfrac{8}{8} \).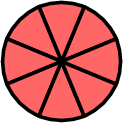
- Subtract the slices eaten by Louis
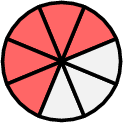
Louis eats 3 slices, which is \( \dfrac{3}{8} \) of the cake. Remaining cake after Louis eats: $$ \dfrac{8}{8} - \dfrac{3}{8} = \dfrac{5}{8}. $$ \(-\) 
\(=\) 
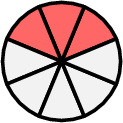- Final Answer:
The fraction of the cake that remains is \( \dfrac{5}{8} \).
Exercise
Today, Louis eats \( \dfrac{1}{2} \) of a croissant. Then, Louis eats \( \dfrac{1}{4} \) of another croissant. How much croissant did Louis eat in total? of a croissant
- Represent the croissants as fractions
Louis eats \( \dfrac{1}{2} \) of the first croissant and \( \dfrac{1}{4} \) of the second croissant. To find the total, add the two fractions: $$ \dfrac{1}{2} + \dfrac{1}{4}. $$ - Find a common denominator
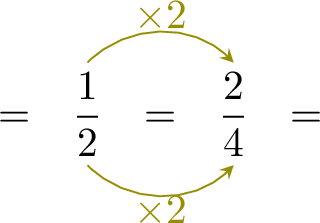
The denominators are 2 and 4. The least common denominator is 4. Convert \( \dfrac{1}{2} \) to a fraction with denominator 4: - Add the fractions
$$\begin{aligned}[t]\dfrac{1}{2}+\dfrac{1}{4} &= \dfrac{2}{4} + \dfrac{1}{4}\\&= \dfrac{3}{4}\end{aligned}$$ \(+\) \(=\) \(+\) \(=\) - Final Answer:
Louis ate a total of \( \dfrac{3}{4} \) of a croissant.
Exercise
At the beginning, there are \( \dfrac{5}{6} \) of a cake. After eating, there are \( \dfrac{2}{3} \) of the cake. What quantity of cake did Louis eat? of the cake
- Represent the cake as fractions
At the beginning, there is \( \dfrac{5}{6} \) of the cake. After eating, \( \dfrac{2}{3} \) of the cake remains. To find the quantity Louis ate, subtract the remaining cake from the initial amount: $$ \dfrac{5}{6} - \dfrac{2}{3}. $$ - Find a common denominator
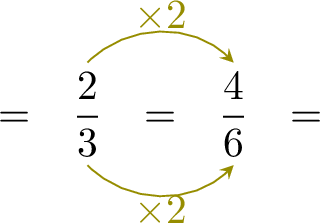
The denominators are 6 and 3. The least common denominator is 6. Convert \( \dfrac{2}{3} \) to a fraction with denominator 6: - Subtract the fractions
$$\begin{aligned}[t]\dfrac{5}{6} - \dfrac{2}{3} &= \dfrac{5}{6} - \dfrac{4}{6}\\&= \dfrac{1}{6}\end{aligned}$$
\(-\) 
\(=\) \(-\) 
\(=\) 
- Final Answer:
Louis ate \( \dfrac{1}{6} \) of the cake.
Exercise
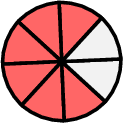
At the beginning, there are \( \dfrac{7}{8} \) of a pizza. After eating, there are \( \dfrac{3}{4} \) of the pizza. What quantity of pizza did Louis eat? of the pizza
- Represent the pizza as fractions
At the beginning, there is \( \dfrac{7}{8} \) of the pizza. After eating, \( \dfrac{3}{4} \) of the pizza remains. To find the quantity Louis ate, subtract the remaining pizza from the initial amount: $$ \dfrac{7}{8} - \dfrac{3}{4}. $$ - Find a common denominator
The denominators are 8 and 4. The least common denominator is 8. Convert \( \dfrac{3}{4} \) to a fraction with denominator 8:
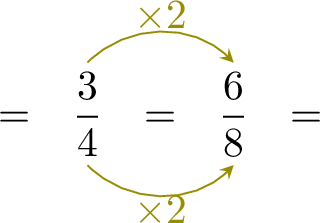
- Subtract the fractions
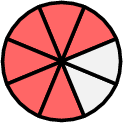
$$\begin{aligned}[t]\dfrac{7}{8} - \dfrac{3}{4} &= \dfrac{7}{8} - \dfrac{6}{8}\\&= \dfrac{1}{8}\end{aligned}$$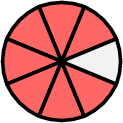
\(-\) \(=\) \(-\) 
\(=\) 
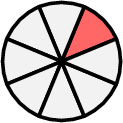
- Final Answer:
Louis ate \( \dfrac{1}{8} \) of the pizza.
Exercise
Louis read \( \dfrac{2}{5} \) of his book on Saturday and \( \dfrac{3}{10} \) of his book on Sunday. How much of his book did Louis read in total? of the book
- Represent the book as fractions
Louis read \( \dfrac{2}{5} \) of the book on Saturday and \( \dfrac{3}{10} \) of the book on Sunday. To find the total, add the two fractions: $$ \dfrac{2}{5} + \dfrac{3}{10}. $$ - Find a common denominator
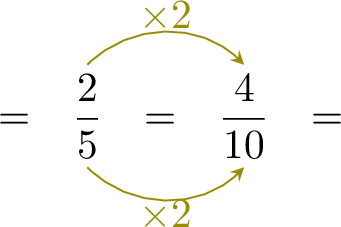
The denominators are 5 and 10. The least common denominator is 10. Convert \( \dfrac{2}{5} \) to a fraction with denominator 10: - Add the fractions
$$\begin{aligned}[t]\dfrac{2}{5} + \dfrac{3}{10} &= \dfrac{4}{10} + \dfrac{3}{10}\\&= \dfrac{7}{10}\end{aligned}$$ \(+\) 
\(=\) 
\(+\) \(=\) - Final Answer:
Louis read a total of \( \dfrac{7}{10} \) of his book.