Angles
What is an Angle?
Comparing Angles
Mcq
Which angle has the greater measure?
The measure of an angle depends on the opening between its rays. A wider opening means a greater angle measure. Angle B has a wider opening (\(120^\circ\)) compared to Angle A (\(30^\circ\)). Therefore, Angle B is greater.
Mcq
Which angle has the greater measure?
The measure of an angle depends on the opening between its rays. A wider opening means a greater angle measure. Angle B has a wider opening (\(100^\circ\)) compared to Angle A (\(30^\circ\)). Therefore, Angle B is greater.
Mcq
Which angle has the greater measure?
The measure of an angle depends on the opening between its rays. A wider opening means a greater angle measure. Angle A has a wider opening (\(170^\circ\)) compared to Angle B (\(80^\circ\)). Therefore, Angle A is greater.
Mcq
Which angle has the greater measure?
The measure of an angle depends on the opening between its rays. A wider opening means a greater angle measure. Angle A has a wider opening (\(60^\circ\)) compared to Angle B (\(30^\circ\)). Therefore, Angle A is greater.
Mcq
Which angle has the greater measure?
The measure of an angle depends on the opening between its rays. A wider opening means a greater angle measure. Angle A has a wider opening (\(90^\circ\)) compared to Angle B (\(30^\circ\)). Therefore, Angle A is greater.
Degrees
Dividing the Full Turn
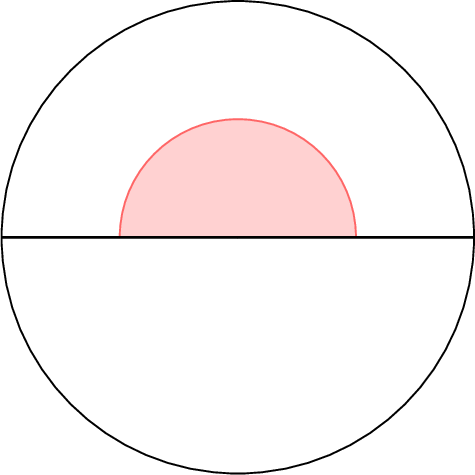
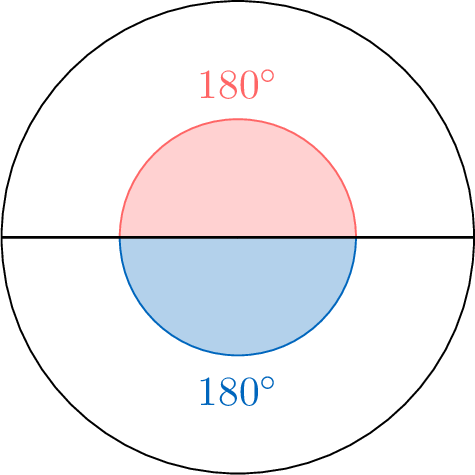
$$\begin{aligned}\text{One-half of a full turn} &= \frac{1}{2} \times 360^\circ \\
&= 360^\circ \div 2 \\
&= 180^\circ\end{aligned}$$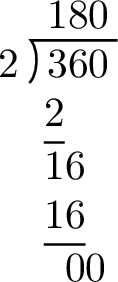
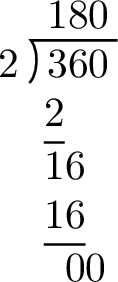

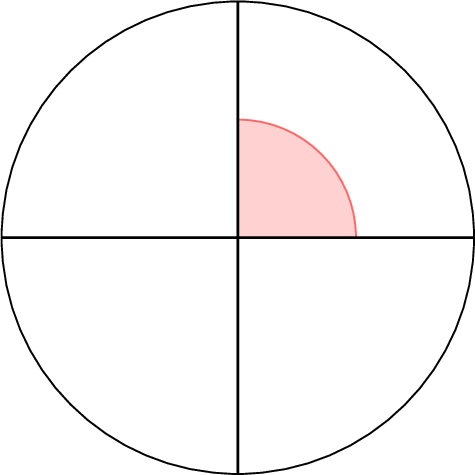
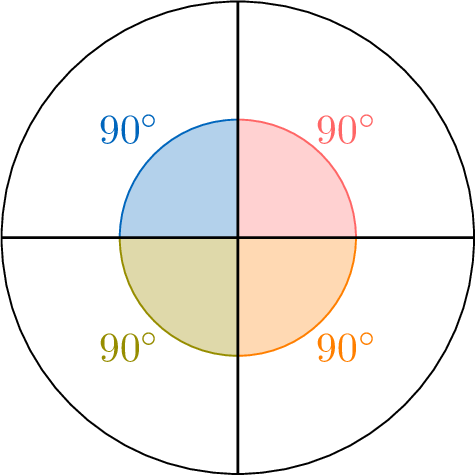
$$\begin{aligned}\text{One-quarter of a full turn} &= \frac{1}{4} \times 360^\circ \\
&= 360^\circ \div 4 \\
&= 90^\circ\end{aligned}$$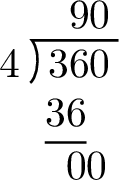
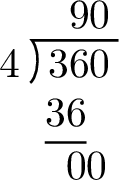

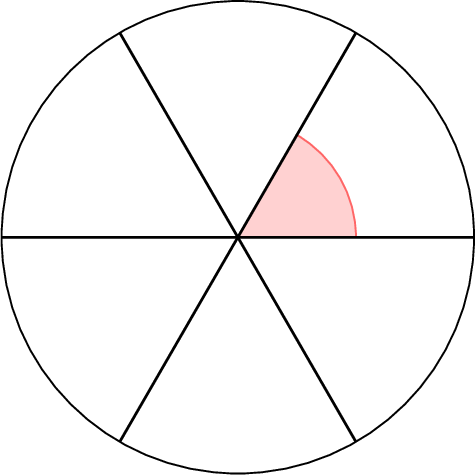
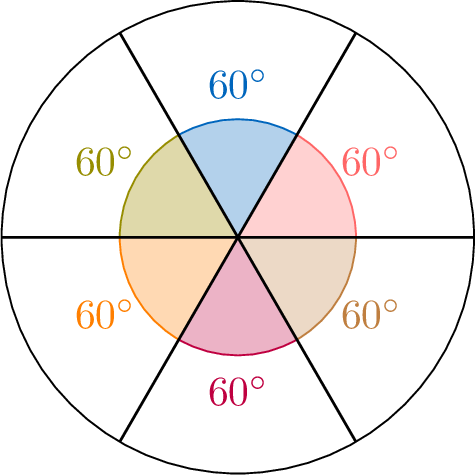
$$\begin{aligned}\text{One-sixth of a full turn} &= \frac{1}{6} \times 360^\circ \\
&= 360^\circ \div 6 \\
&= 60^\circ\end{aligned}$$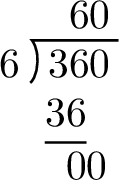
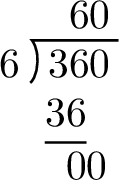

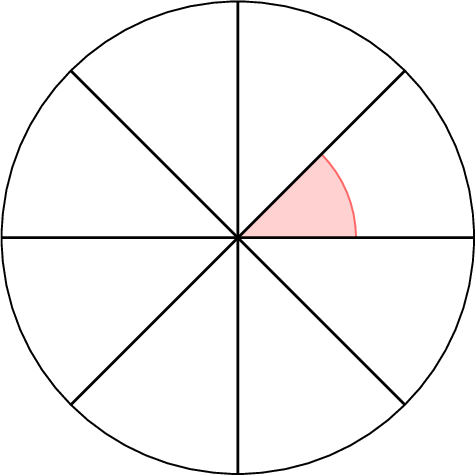
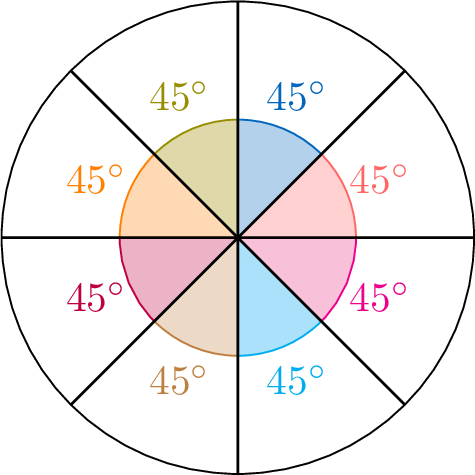
$$\begin{aligned}\text{One-eighth of a full turn} &= \frac{1}{8} \times 360^\circ \\
&= 360^\circ \div 8 \\
&= 45^\circ\end{aligned}$$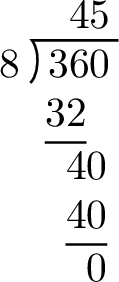
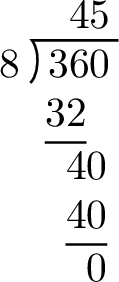

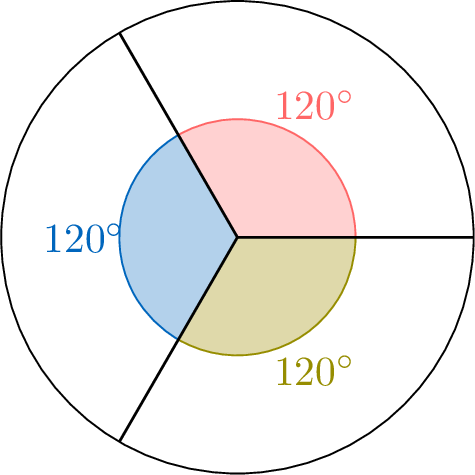
$$\begin{aligned}\text{One-third of a full turn} &= \frac{1}{3} \times 360^\circ \\
&= 360^\circ \div 3 \\
&= 120^\circ\end{aligned}$$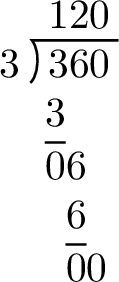
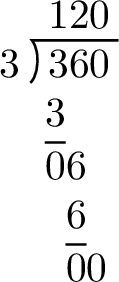

Measuring and Drawing Angles with a Protractor
Measuring Angles
Exercise
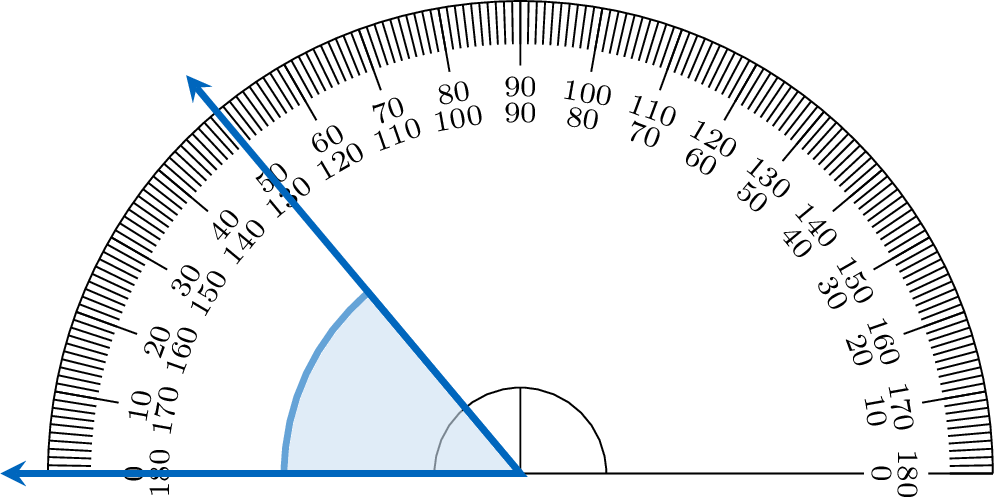
To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(50^\circ\), so the angle measures \(50^\circ\).
Exercise
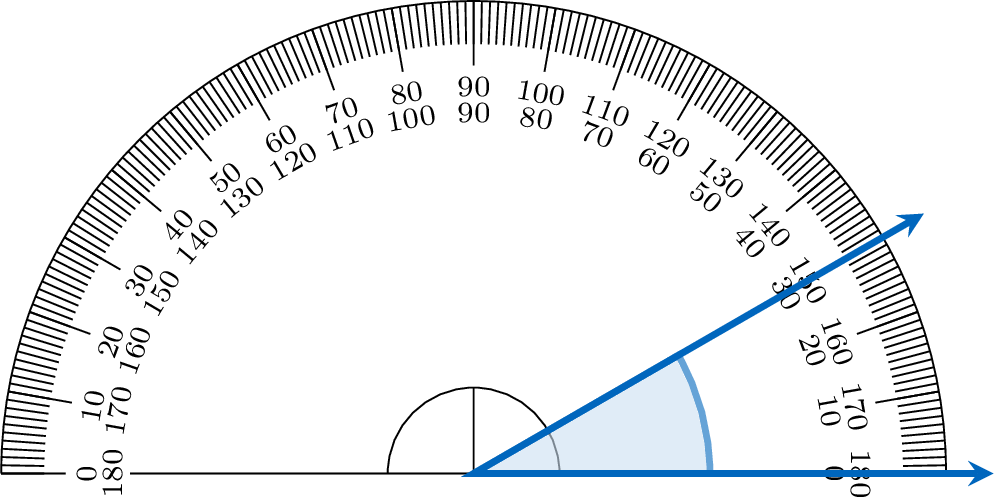
To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(30^\circ\), so the angle measures \(30^\circ\).
Exercise

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(100^\circ\), so the angle measures \(100^\circ\).
Exercise
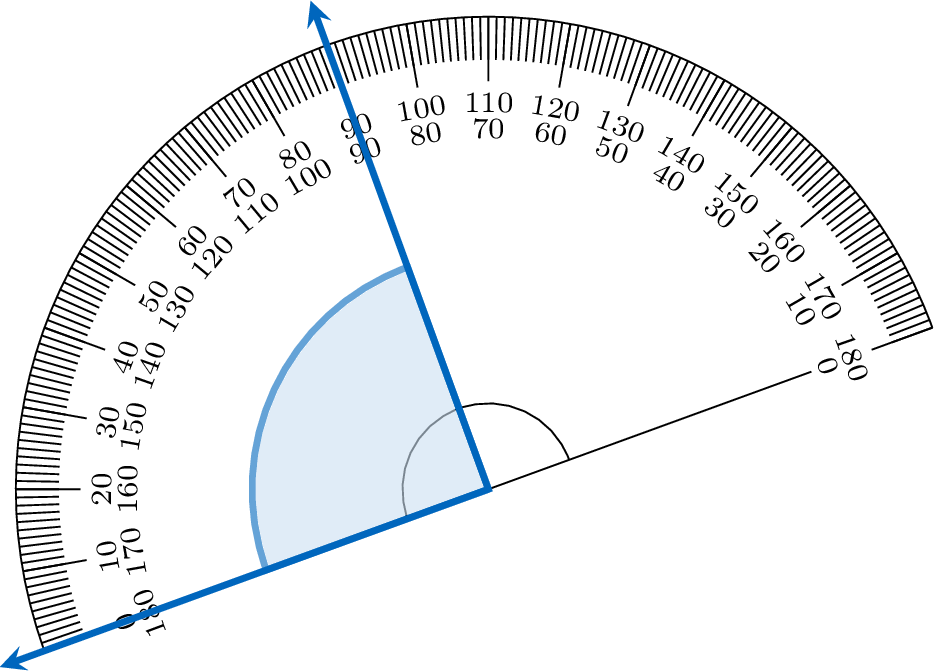
To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(90^\circ\), so the angle measures \(90^\circ\).
Exercise
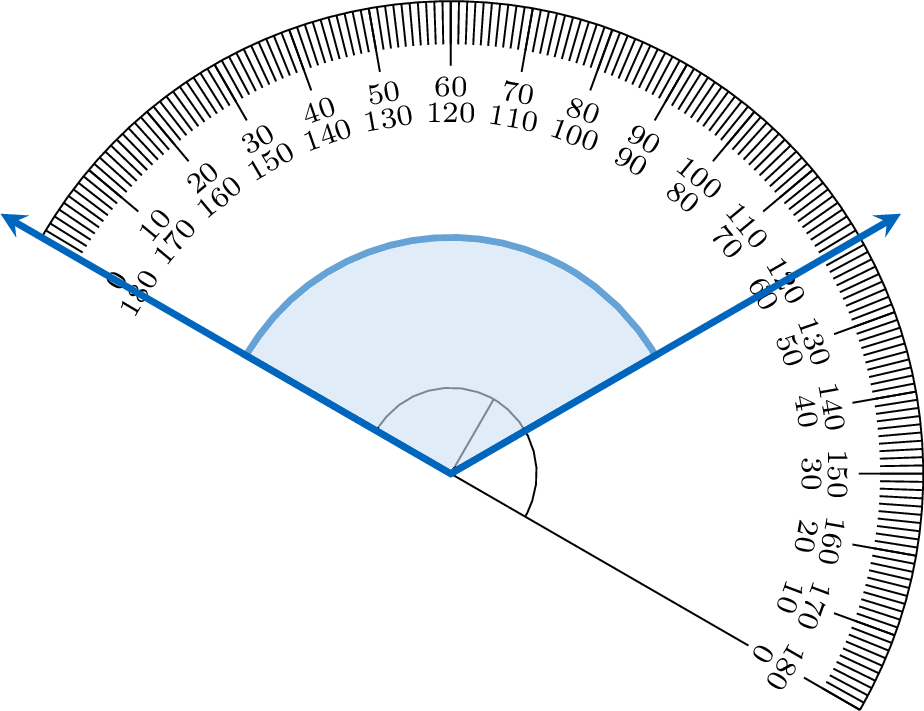
To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(120^\circ\), so the angle measures \(120^\circ\).
Exercise
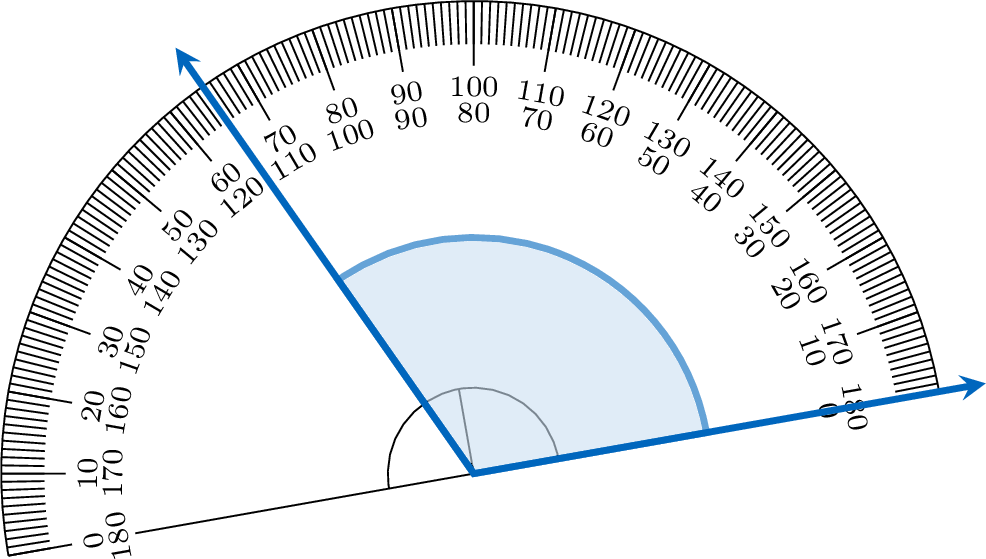
To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(115^\circ\), so the angle measures \(115^\circ\).
Exercise

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale. Here, one ray aligns with \(0^\circ\), and the other points to \(45^\circ\), so the angle measures \(45^\circ\).
Measuring Angles
Mcq
Using a protractor, find the measure of the angle shown.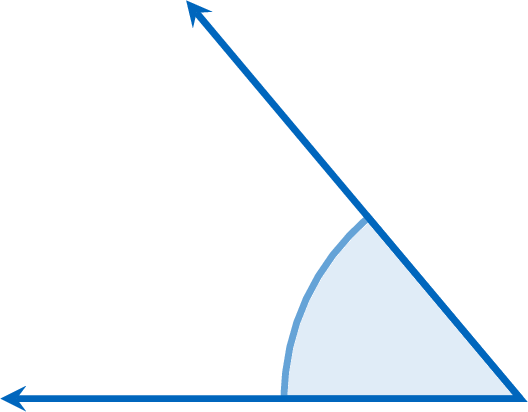

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale.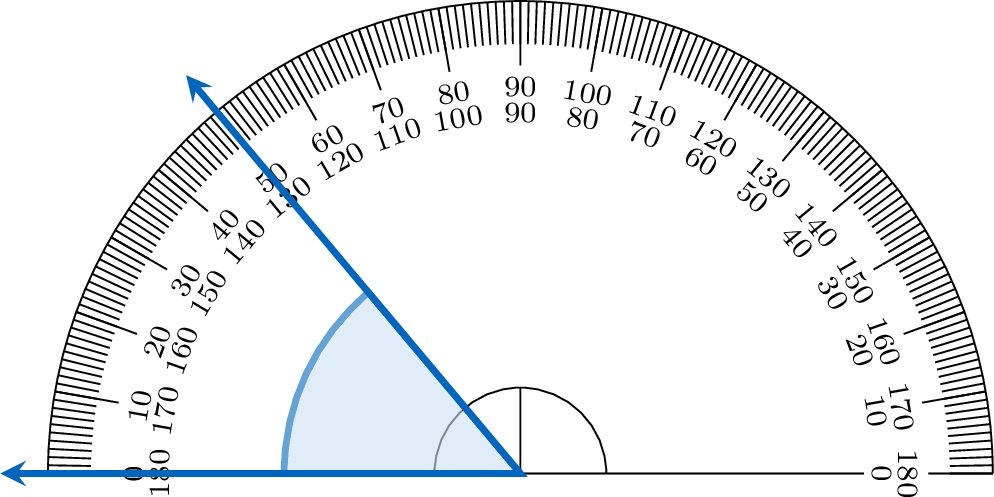

Mcq
Using a protractor, find the measure of the angle shown.

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale.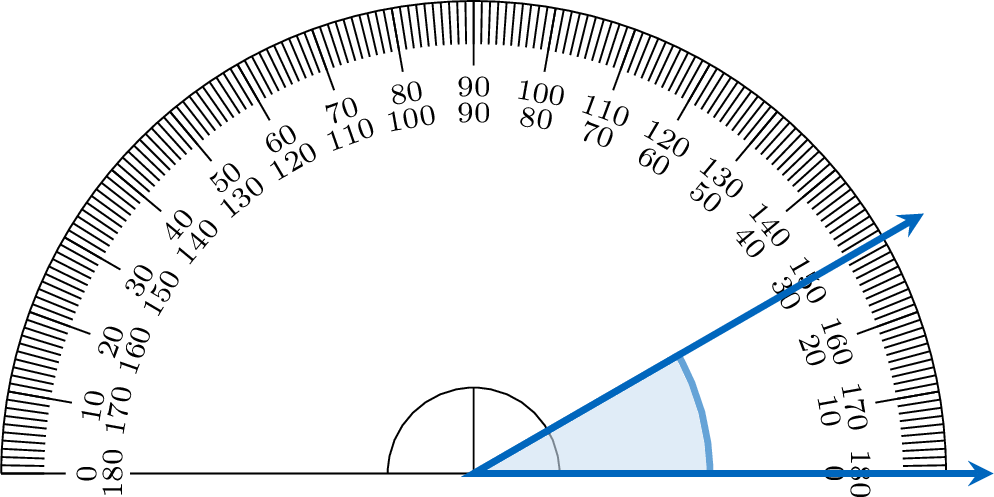

Mcq
Using a protractor, find the measure of the angle shown.

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale.

Mcq
Using a protractor, find the measure of the angle shown.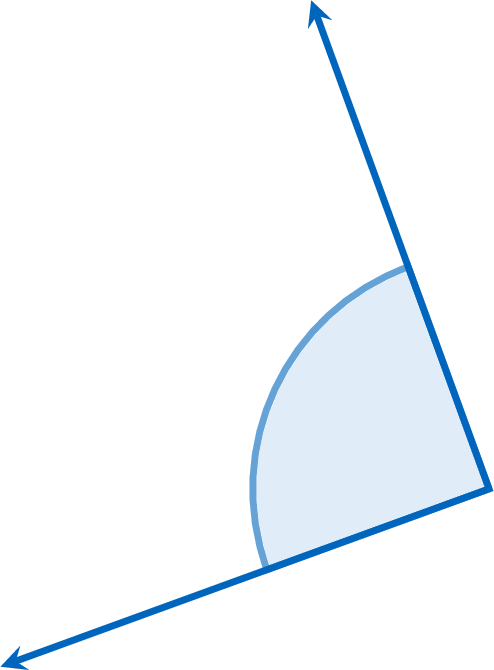

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale.

Mcq
Using a protractor, find the measure of the angle shown.

To measure an angle with a protractor, place its center on the vertex and align one ray with the \(0^\circ\) mark. The other ray points to the angle’s measure on the protractor’s scale.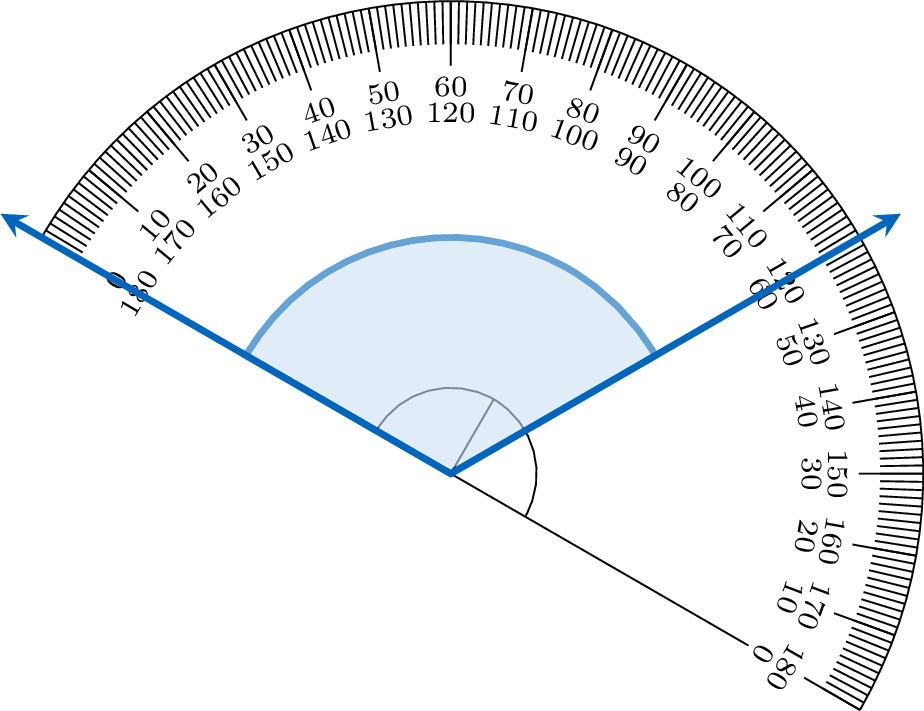

Constructing Angles
Exercise
Using a pencil, a ruler, and a protractor, draw an angle that measures \(90^\circ\).
To draw a \(90^\circ\) angle:
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(90^\circ\) on the protractor’s scale.
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Exercise
Using a pencil, a ruler, and a protractor, draw an angle that measures \(60^\circ\).
To draw a \(60^\circ\) angle: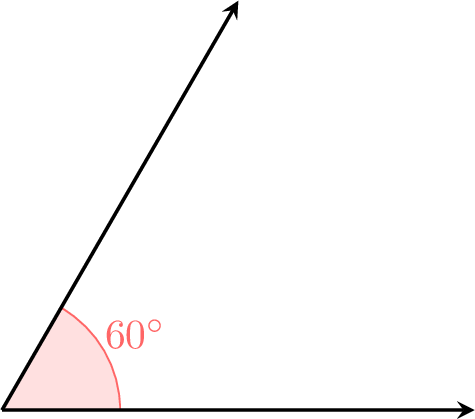
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(60^\circ\) on the protractor’s scale.
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Exercise
Using a pencil, a ruler, and a protractor, draw an angle that measures \(120^\circ\).
To draw a \(120^\circ\) angle: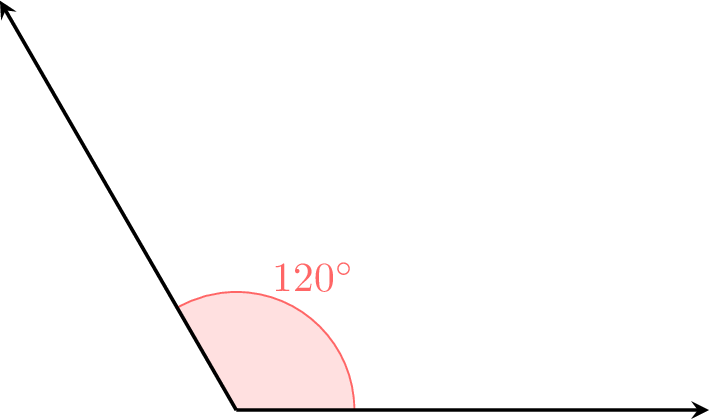
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(120^\circ\) on the protractor’s scale.
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Exercise
Using a pencil, a ruler, and a protractor, draw an angle that measures \(45^\circ\).
To draw a \(45^\circ\) angle: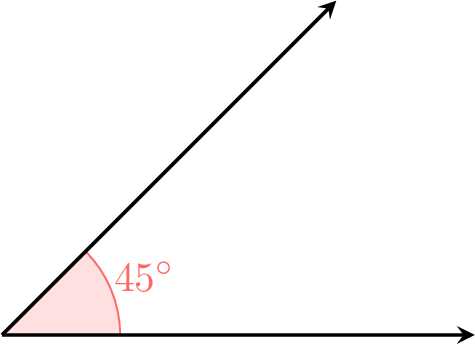
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(45^\circ\) on the protractor’s scale.
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Classification of Angles
Identifying Angle Types by Measure
Mcq
What is the nature of the marked angle?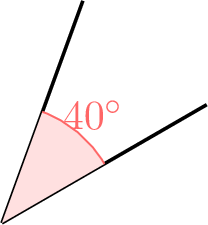

- An acute angle measures less than 90 degrees.
- The marked angle, measuring \(40^\circ\), is acute because it is less than \(90^\circ\).
Mcq
What is the nature of the marked angle?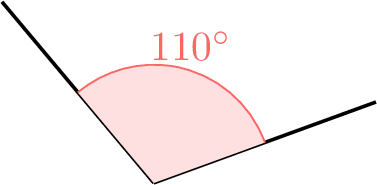

- An obtuse angle measures more than 90 degrees but less than 180 degrees.
- The marked angle, measuring \(110^\circ\), is obtuse because it is between \(90^\circ\) and \(180^\circ\).
Mcq
What is the nature of the marked angle?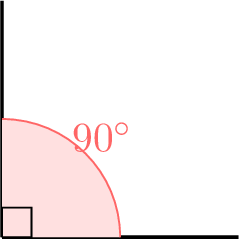

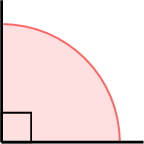
- A right angle measures exactly 90 degrees.
- The marked angle, measuring \(90^\circ\), is a right angle.
Mcq
What is the nature of the marked angle?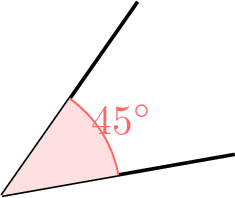

- An acute angle measures less than 90 degrees.
- The marked angle, measuring \(45^\circ\), is acute because it is less than \(90^\circ\).
Mcq
What is the nature of the marked angle?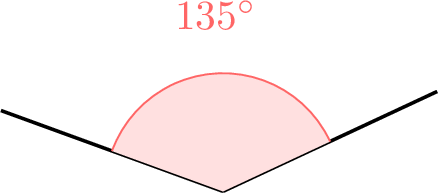

- An obtuse angle measures more than 90 degrees but less than 180 degrees.
- The marked angle, measuring \(135^\circ\), is obtuse because it is between \(90^\circ\) and \(180^\circ\).
Identifying Angle Types
Mcq
Identify the type of the highlighted angle. 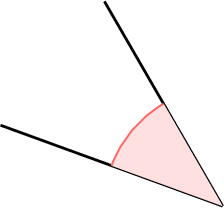
Choose one answer:

- An acute angle measures less than \(90^\circ\).
- The highlighted angle (\(\approx 40^\circ\)) is less open than a right angle
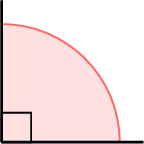 .
. - Hence it is acute.
Mcq
Identify the type of the highlighted angle. 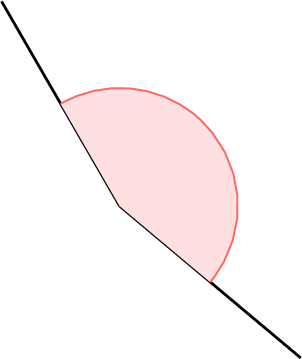
Choose one answer:

- An obtuse angle measures between \(90^\circ\) and \(180^\circ\).
- The highlighted angle (\(\approx160^\circ\)) is more open than a right angle
 but less than a straight angle
but less than a straight angle  .
. - Therefore it is obtuse.
Mcq
Identify the type of the highlighted angle. 
Choose one answer:

- A straight angle measures exactly \(180^\circ\).
- The highlighted angle forms a line.
- It is therefore straight.
Mcq
Identify the type of the highlighted angle. 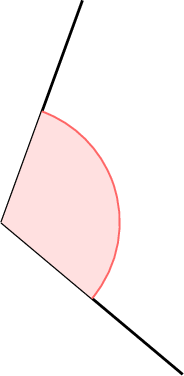
Choose one answer:

- An obtuse angle measures between \(90^\circ\) and \(180^\circ\).
- The highlighted angle (\(\approx110^\circ\)) is more open than a right angle
 but less open than a straight angle
but less open than a straight angle  .
. - Therefore it is obtuse.
Constructing Angle Types
Exercise
Using a pencil, a ruler, and a protractor, draw an acute angle.
To draw an acute angle, such as a \(40^\circ\) angle: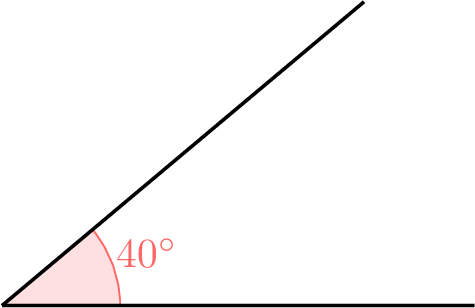
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(40^\circ\) on the protractor’s scale (any angle less than \(90^\circ\) is acceptable).
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Exercise
Using a pencil, a ruler, and a protractor, draw an obtuse angle.
To draw an obtuse angle, such as a \(120^\circ\) angle: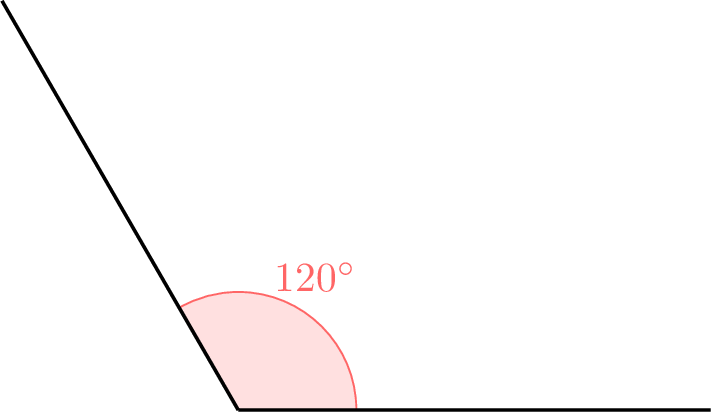
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(120^\circ\) on the protractor’s scale (any angle greater than \(90^\circ\) but less than \(180^\circ\) is acceptable).
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.

Exercise
Using a pencil, a ruler, and a protractor, draw a right angle.
To draw a right angle, which measures \(90^\circ\):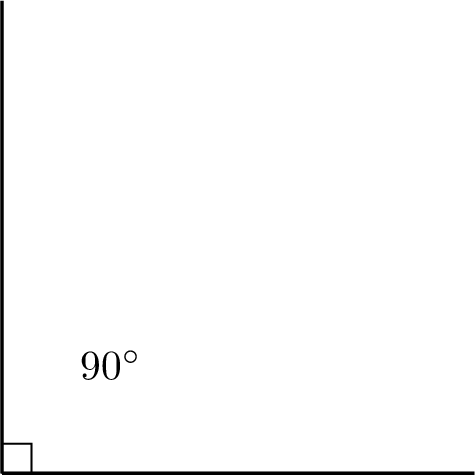
- Draw a ray using a ruler to create the first side of the angle.
- Place the protractor’s center on the endpoint of the ray (the vertex) and align the baseline with the ray at \(0^\circ\).
- Mark a point at \(90^\circ\) on the protractor’s scale.
- Remove the protractor and use the ruler to draw a second ray from the vertex through the marked point.