Set Theory

Definitions

Definition Set

A set is a collection of objects, called elements.
We list its elements between curly brackets.

Example

List all possible results when rolling a standard die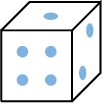

Answer

$E=\{1,2,3,4,5,6\}=\{$

$\}$.

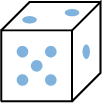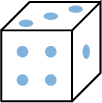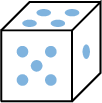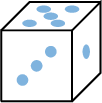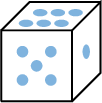Definition Element

An element is an object contained in a set.
$\in$ means "is an element of" or "belongs to".
$\notin$ means "is not an element of" or "does not belong to".

Example

$2\in \{1,2,3,4,5,6\}$ and $7\notin \{1,2,3,4,5,6\}$.

Definition Equal sets

Two sets are equal if they have exactly the same elements.

Example

Determine if the sets $\{2,6,4\}$ and $\{2,4,6\}$ are equal.

Answer

Yes, the sets $\{2,6,4\}$ and $\{2,4,6\}$ are equal because they contain the same elements: $2$, $4$, and $6$.

Example

Determine if the sets $\{1,2,3\}$ and $\{1,2,4\}$ are equal.

Answer

No, the sets $\{1,2,3\}$ and $\{1,2,4\}$ are not equal because element $3$ belongs to $\{1,2,3\}$ but not to $\{1,2,4\}$.

Cardinality

Definition Cardinality

$\Card{A}$ denotes the number of elements in the set $A$.

Example

$\Card{\{1,2,3,4,5,6\}}=6=$

Complement

Definition Universal set

A universal set is the set of all elements considered.

Definition Complement

The complement of a set $A$, denoted $A'$, consists of all elements in $U$ that are not in $A$. Sets $A$ and $A'$ are said to be complementary.

Example

Given the universe $U = \{1, 2, 3, 4, 5, 6\}$ and the set $A = \{1, 3, 5\}$, find the complement $A'$.

Answer

Start with the universe $U = \{1, 2, 3, 4, 5, 6\}$.
The set $A = \{1, 3, 5\}$ includes 1, 3, and 5.
The complement $A'$ is all the elements in $U$ that are not in $A$:
$$A' = \{2, 4, 6\}$$