Long Multiplication
Long multiplication is a method used for multiplying larger numbers. It requires knowledge of the multiplication table for single digits.
Multiplication Tables for Multiples of 10
Imagine starting with a simple one-digit number, such as 3. What happens when we multiply by multiples of 10? Let’s explore step by step:
-
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{3}0\) -
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{6}0\) -
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{3}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{9}0\) - \(\textcolor{colordef}{3}\times \textcolor{colorprop}{4}0=\textcolor{olive}{12}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{5}0=\textcolor{olive}{15}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{6}0=\textcolor{olive}{18}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{7}0=\textcolor{olive}{21}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{8}0=\textcolor{olive}{24}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{9}0=\textcolor{olive}{27}0\)
Proposition Multiplication Table for Multiple of 10
To multiply by multiples of 10, use the regular multiplication table and add the zeros from the factors to the result:\(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}&=\textcolor{olive}{3}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}&=\textcolor{olive}{6 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}&=\textcolor{olive}{9 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}&=\textcolor{olive}{12 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}&=\textcolor{olive}{15 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27 }\\\end{aligned}\) \(\quad\) \(\begin{aligned}\textcolor{colordef}{3}00\times \textcolor{colorprop}{1}0&=\textcolor{olive}{3}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{2}0&=\textcolor{olive}{6}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{3}0&=\textcolor{olive}{9}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{4}0&=\textcolor{olive}{12}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{5}0&=\textcolor{olive}{15}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{6}0&=\textcolor{olive}{18}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{7}0&=\textcolor{olive}{21}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{8}0&=\textcolor{olive}{24}000\\\textcolor{colordef}{3}00\times \textcolor{colorprop}{9}0&=\textcolor{olive}{27}000\\\end{aligned}\)
Long Multiplication by One-Digit Numbers
When multiplying a large number by a single-digit number, it can be tedious and time-consuming to handle each step separately. For example: 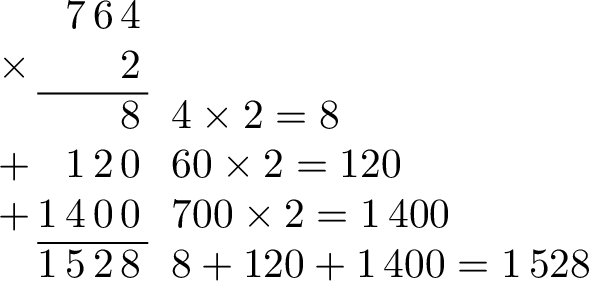
To simplify, you can perform the additions step by step using the carry-over method, similar to column addition.
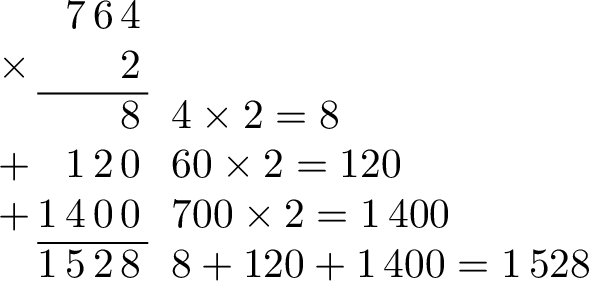
Method Column Multiplication
To calculate \(23 \times 7\), follow these steps:
- Step 1: Write the multiplication in columns
Write the numbers in columns, aligning the digits based on their place value (units, tens, hundreds).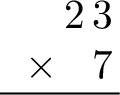
- Step 2: Multiply the ones
$$\textcolor{colordef}{3} \text{ ones} \times \textcolor{colordef}{7} \text{ ones} = 21 \text{ ones} = \textcolor{olive}{2} \text{ tens} + \textcolor{colorprop}{1} \text{ one}$$ Write the carry-over (\(\textcolor{olive}{2}\)) above the tens column.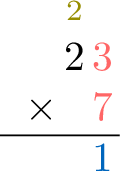
- Step 3: Multiply the tens
$$\textcolor{colordef}{2} \text{ tens} \times \textcolor{colordef}{7} \text{ ones} + \textcolor{olive}{2} \text{ tens (carry-over)} = \textcolor{colorprop}{16} \text{ tens}$$ Write \(\textcolor{colorprop}{16}\) in the tens and hundreds columns.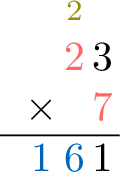
- Result: \(23 \times 7 = 161\).
Long Multiplication by Multi-Digit Numbers
To calculate \(23 \times 37\), we can use the distributive property:$$\begin{aligned}23 \times 37 &= \textcolor{colorprop}{23 \times 7} + \textcolor{colordef}{23 \times 30} & & \text{(by distributivity: } 37 = 7 + 30) \\&= \textcolor{colorprop}{161} + \textcolor{colordef}{690} & & \text{(intermediate products)} \\&= 851 && \text{(add the intermediate results)} \\\end{aligned}$$This approach forms the basis of column multiplication for multi-digit numbers. The process organizes the steps efficiently: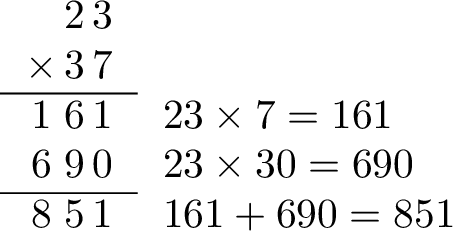
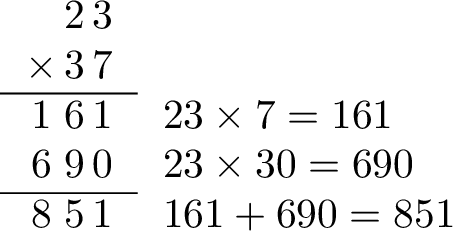
Method Column Multiplication for Multi-Digit Numbers
To calculate \(23 \times 37\), follow these steps:
- Step 1: Write the multiplication in columns
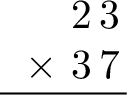
- Step 2: Multiply the ones digit (7)
- Multiply the ones: \(\textcolor{colordef}{3} \times \textcolor{colordef}{7} = \textcolor{olive}{2}\textcolor{colorprop}{1}\)
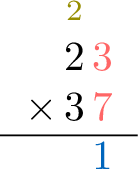
- Multiply the tens: \(\textcolor{colordef}{2} \times \textcolor{colordef}{7} + \textcolor{colordef}{\scriptstyle 2}\text{\scriptsize(carried)} = 14 + 2 = \textcolor{colorprop}{16}\)
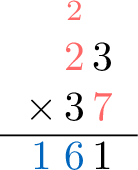
- Multiply the ones: \(\textcolor{colordef}{3} \times \textcolor{colordef}{7} = \textcolor{olive}{2}\textcolor{colorprop}{1}\)
- Step 3: Multiply the tens digit (3)
- Add a placeholder . (or 0) as a for the multiplication with a tens digit
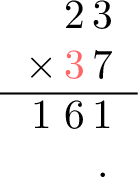
- Multiply the ones: \(\textcolor{colordef}{3} \times \textcolor{colordef}{3}= \textcolor{colorprop}{9}\)
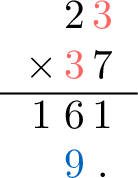
- Multiply the tens: \(\textcolor{colordef}{2} \times \textcolor{colordef}{3}= \textcolor{colorprop}{6}\)
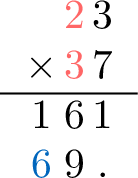
- Add a placeholder . (or 0) as a for the multiplication with a tens digit
- Step 4: Add the intermediate results \(\textcolor{colordef}{161} + \textcolor{colordef}{690} = \textcolor{colorprop}{851}\)
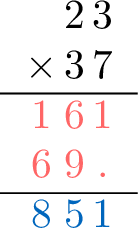
- Result: \(23 \times 37 = 851\).