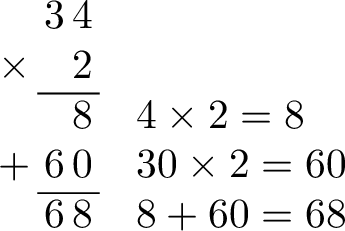Long Multiplication
Long multiplication is a method used for multiplying larger numbers. It requires knowledge of the multiplication table for single digits.
Multiplication Tables for Multiples of 10
Imagine starting with a simple one-digit number, such as 3. What happens when we multiply by multiples of 10? Let’s explore step by step:
-
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{3}0\) -
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{6}0\) -
\(\textcolor{colordef}{3}\times \textcolor{colorprop}{3}0\) \(=\) \(\textcolor{colordef}{3}\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\) \(\textcolor{olive}{9}0\) - \(\textcolor{colordef}{3}\times \textcolor{colorprop}{4}0=\textcolor{olive}{12}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{5}0=\textcolor{olive}{15}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{6}0=\textcolor{olive}{18}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{7}0=\textcolor{olive}{21}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{8}0=\textcolor{olive}{24}0\)
- \(\textcolor{colordef}{3}\times \textcolor{colorprop}{9}0=\textcolor{olive}{27}0\)
Proposition Multiplication Table for Multiples of 10
The multiplication table for multiples of 10 is the same as the regular table, but with a zero added at the end:\(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}&=\textcolor{olive}{3}\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}&=\textcolor{olive}{6 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}&=\textcolor{olive}{9 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}&=\textcolor{olive}{12 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}&=\textcolor{olive}{15 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}&=\textcolor{olive}{18 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}&=\textcolor{olive}{21 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}&=\textcolor{olive}{24 }\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}&=\textcolor{olive}{27 }\\\end{aligned}\) \(\quad\) \(\begin{aligned}\textcolor{colordef}{3}\times \textcolor{colorprop}{1}0&=\textcolor{olive}{3}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{2}0&=\textcolor{olive}{6}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{3}0&=\textcolor{olive}{9}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{4}0&=\textcolor{olive}{12}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{5}0&=\textcolor{olive}{15}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{6}0&=\textcolor{olive}{18}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{7}0&=\textcolor{olive}{21}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{8}0&=\textcolor{olive}{24}0\\\textcolor{colordef}{3}\times \textcolor{colorprop}{9}0&=\textcolor{olive}{27}0\\\end{aligned}\)
Long Multiplication by One-Digit Numbers
How do we multiply a two-digit number by a one-digit number? For example, to calculate \(2 \times 34\), we can break the problem into simpler parts:
| \(2 \times 34\) | \(=\) | \(2 \times\) 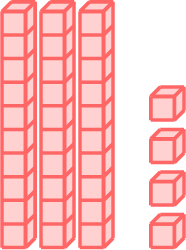 |
| \(=\) | \(2 \times\)  \(+ 2 \times\) \(+ 2 \times\) | |
| \(=\) |  \(+\) \(+\) | |
| \(=\) | \(60+8\) | |
| \(=\) | \(68\) |
Method Long Multiplication by One-Digit Numbers
- Set up column multiplication: Align the digits by their place value (ones, tens, etc.):
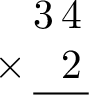
- Multiply the ones place: Multiply the ones digit of the top number by the one-digit multiplier:
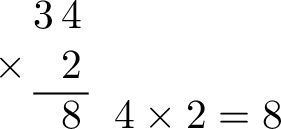
- Multiply the tens place: Multiply the tens digit of the top number by the one-digit multiplier:
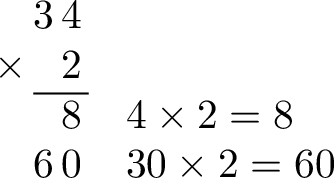
- Add the results: Sum the partial results to find the final product: