Properties of Integers
Division with Remainders
Hugo has \(\textcolor{olive}{13}\) marbles to divide evenly into \(\textcolor{colordef}{3} \) groups. 
How many marbles will be in each group, and how many will be left over?
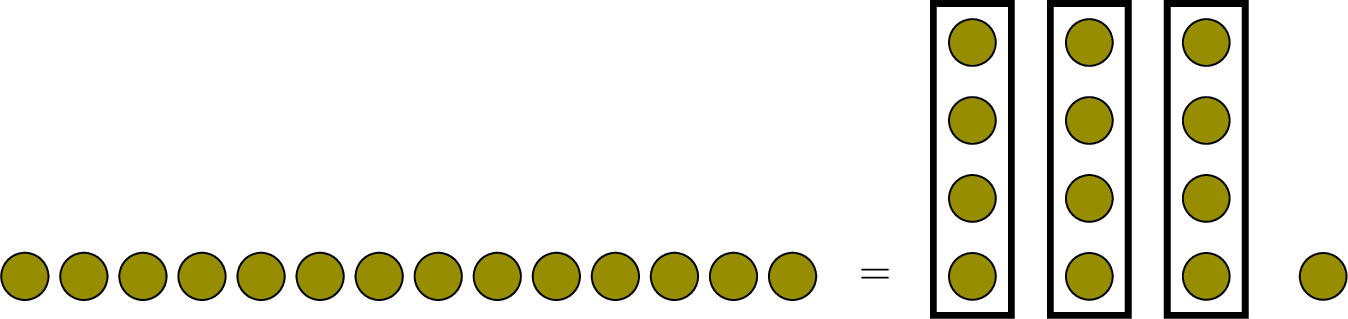
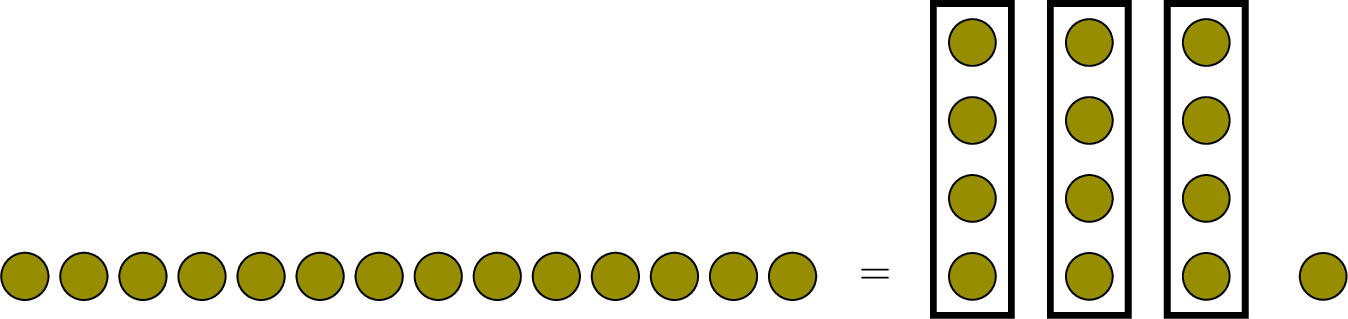
Theorem Division with Remainder
For any two whole numbers, a \(\textcolor{olive}{\text{dividend}}\) and a non-zero \(\textcolor{colordef}{\text{divisor}}\), there exists a unique \(\textcolor{colorprop}{\text{quotient}}\) and a unique \(\textcolor{orange}{\text{remainder}}\) that are also whole numbers, such that: $$\begin{array}{ccccccccl} \textcolor{olive}{13} &=& \textcolor{colordef}{3}& \times& \textcolor{colorprop}{4}&+&\textcolor{orange}{1} & \text{with }& \textcolor{orange}{1}\lt \textcolor{colordef}{3}\\ \textcolor{olive}{\text{Dividend}}&=& \textcolor{colordef}{\text{Divisor}}&\times&\textcolor{colorprop}{\text{Quotient}}&+&\textcolor{orange}{\text{Remainder}}& \text{with }& \textcolor{orange}{\text{Remainder}}\lt \textcolor{colordef}{\text{Divisor}} \end{array} $$ 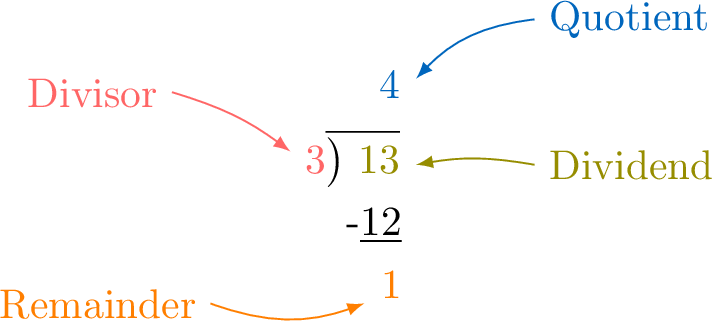
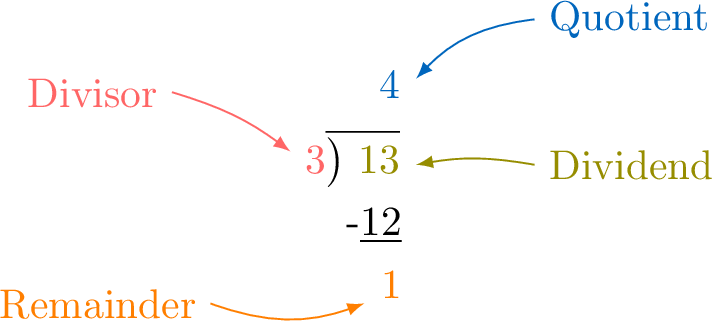
Divisibility
Definition Divisible
A whole number is said to be divisible by another non-zero whole number if the remainder is zero when you divide the first number by the second number. In this case, we say that the second number is a divisor of the first number.
Example
Is \(10\) divisible by \(5\)?
Yes, \(\textcolor{olive}{10}\) is divisible by \(\textcolor{colordef}{5}\) because the remainder of the division is \(\textcolor{orange}{0}\): \(\textcolor{olive}{10} = \textcolor{colordef}{5} \times \textcolor{colorprop}{2} + \textcolor{orange}{0}\).
Example
Is \(13\) divisible by \(5\)?
No, \(\textcolor{olive}{13}\) is not divisible by \(\textcolor{colordef}{5}\) because the remainder of the division is \(\textcolor{orange}{3}\): \(\textcolor{olive}{13} = \textcolor{colordef}{5} \times \textcolor{colorprop}{2} + \textcolor{orange}{3}\).
Definition Multiple
A whole number is said to be a multiple of another non-zero whole number if the first number can be obtained by multiplying the second number by some whole number. In other words, the first number appears in the multiplication table of the second number. In this case, we say that the second number is a factor of the first number.
Example
Is \(10\) a multiple of \(5\)?
Yes, \(10\) is a multiple of \(5\) because \(5 \times 2 = 10\). So \(5\) is a factor of \(10\).
Theorem Divisible \(\Leftrightarrow\) Multiple
For two whole numbers, the first number is divisible by the second number if and only if the first number is a multiple of the second number.
This is a direct consequence of the uniqueness of the quotient and remainder in the division with remainder theorem. If the remainder is zero, then the dividend is exactly the product of the divisor and the quotient, which is the definition of a multiple. Conversely, if a number is a multiple of another, then by definition it can be written as a product, implying a zero remainder upon division.
Example
Is \(1000\) divisible by \(10\)?
Yes, as \(1000 = 100 \times 10\), \(1000\) is a multiple of \(10\). Therefore, \(1000\) is divisible by \(10\).
Divisibility Criteria
Divisibility criteria are methods that allow us to quickly determine if a whole number is divisible by another whole number without performing long division. These rules are useful for simplifying calculations and understanding number properties. Here are some common divisibility criteria:
Proposition Divisibility Criteria for 2 and 5
- A number is divisible by 2 if its last digit is even (0, 2, 4, 6, or 8).
- A number is divisible by 5 if its last digit is 0 or 5.
Example
Determine whether \(946\) is divisible by \(2\).
\(946\) is divisible by \(2\) because its last digit is \(6\), which is even.
Example
Determine whether \(947\) is divisible by \(5\).
\(947\) is not divisible by \(5\) because its last digit is \(7\), which is not \(0\) or \(5\).
Proposition Divisibility Criteria for 3 and 9
- A number is divisible by 3 if the sum of its digits is divisible by 3.
- A number is divisible by 9 if the sum of its digits is divisible by 9.
Example
Determine whether \(948\) is divisible by \(3\).
\(948\) is divisible by \(3\) because the sum of its digits, \(9 + 4 + 8 = 21\), is divisible by \(3\) (\(21 = 3 \times 7\)).
Example
Determine whether \(948\) is divisible by \(9\).
\(948\) is not divisible by \(9\) because the sum of its digits, \(9 + 4 + 8 = 21\), is not divisible by \(9\) (\(21 = 9 \times 2 + 3\)).
Proposition Divisibility Criteria for 4
A number is divisible by 4 if the number formed by its last two digits is divisible by 4.
Example
Determine whether \(917\) is divisible by \(4\).
\(917\) is not divisible by \(4\) because the number formed by its last two digits, \(17\), is not divisible by \(4\) (\(17 = 4 \times 4 + 1\)).