Proportionality
Definition
Suppose you are making fresh orange juice. The recipe calls for \(\textcolor{colorprop}{2}\) oranges to make \(\textcolor{colordef}{1}\) glass of juice. If you have \(\textcolor{colorprop}{4}\) oranges, you can make \(\textcolor{colordef}{2}\) glasses of juice. With \(\textcolor{colorprop}{6}\) oranges, you can make \(\textcolor{colordef}{3}\) glasses, and so on. The number of glasses of juice you can make increases in direct proportion to the number of oranges you have. This means that the ratio of the number of oranges to the number of glasses is always the same.
In this case:$$\frac{\textcolor{colorprop}{\text{Number of Oranges}}}{\textcolor{colordef}{\text{Number of Glasses}}} = \frac{\textcolor{colorprop}{2}}{\textcolor{colordef}{1}} = \frac{\textcolor{colorprop}{4}}{\textcolor{colordef}{2}} = \frac{\textcolor{colorprop}{6}}{\textcolor{colordef}{3}} = \textcolor{olive}{2 \text{ oranges per glass}}$$The constant ratio here is \(\textcolor{olive}{2}\) oranges per glass, which shows a proportional relationship between the number of oranges and the number of glasses of juice.
In this case:$$\frac{\textcolor{colorprop}{\text{Number of Oranges}}}{\textcolor{colordef}{\text{Number of Glasses}}} = \frac{\textcolor{colorprop}{2}}{\textcolor{colordef}{1}} = \frac{\textcolor{colorprop}{4}}{\textcolor{colordef}{2}} = \frac{\textcolor{colorprop}{6}}{\textcolor{colordef}{3}} = \textcolor{olive}{2 \text{ oranges per glass}}$$The constant ratio here is \(\textcolor{olive}{2}\) oranges per glass, which shows a proportional relationship between the number of oranges and the number of glasses of juice.
Definition Proportional
Two variables \(\textcolor{colordef}{x}\) and \(\textcolor{colorprop}{y}\) are proportional if the ratio of the two variables is equal to a constant value \(\textcolor{olive}{k}\) called the coefficient of proportionality.$$\dfrac{\textcolor{colorprop}{y}}{\textcolor{colordef}{x}} = \textcolor{olive}{k}$$
Example
Determine if the table is proportional
| \(\textcolor{colordef}{x}\) | \(\textcolor{colordef}{1}\) | \(\textcolor{colordef}{2}\) | \(\textcolor{colordef}{3}\) |
| \(\textcolor{colorprop}{y}\) | \(\textcolor{colorprop}{15}\) | \(\textcolor{colorprop}{30}\) | \(\textcolor{colorprop}{45}\) |
As all ratios are equal: \(\dfrac{\textcolor{colorprop}{15}}{\textcolor{colordef}{1}} = \dfrac{\textcolor{colorprop}{30}}{\textcolor{colordef}{2}} = \dfrac{\textcolor{colorprop}{45}}{\textcolor{colordef}{3}} = \textcolor{olive}{15}\), it is a proportional table.
Linearity
Suppose \(\textcolor{colordef}{1}\) cookie costs \(\textcolor{colorprop}{2}\) dollars, which means the coefficient of proportionality is \(\textcolor{olive}{2} = \dfrac{\textcolor{colorprop}{2}}{\textcolor{colordef}{1}}\).So,
| \(\textcolor{colordef}{1}\) cookie costs | \(\textcolor{colorprop}{2} = \textcolor{olive}{2} \times \textcolor{colordef}{1}\) |
| \(\textcolor{colordef}{2}\) cookies cost | \(\textcolor{colorprop}{4} = \textcolor{olive}{2} \times \textcolor{colordef}{2}\) |
| \(\textcolor{colordef}{3}\) cookies cost | \(\textcolor{colorprop}{6} = \textcolor{olive}{2} \times \textcolor{colordef}{3}\) |
| \(\textcolor{colordef}{4}\) cookies cost | \(\textcolor{colorprop}{8} = \textcolor{olive}{2} \times \textcolor{colordef}{4}\) |
| \(\textcolor{colordef}{x}\) cookies cost | \(\textcolor{colorprop}{y} = \textcolor{olive}{2} \times \textcolor{colordef}{x}\) |
Proposition Linearity
Two variables \(\textcolor{colordef}{x}\) and \(\textcolor{colorprop}{y}\) are proportional with coefficient of proportionality \(\textcolor{olive}{k}\) if and only if$$\textcolor{colorprop}{y} = \textcolor{olive}{k}\textcolor{colordef}{x}.$$
Example
For the relation \(\textcolor{colorprop}{y} = \textcolor{olive}{2}\textcolor{colordef}{x}\), we have the following table of values: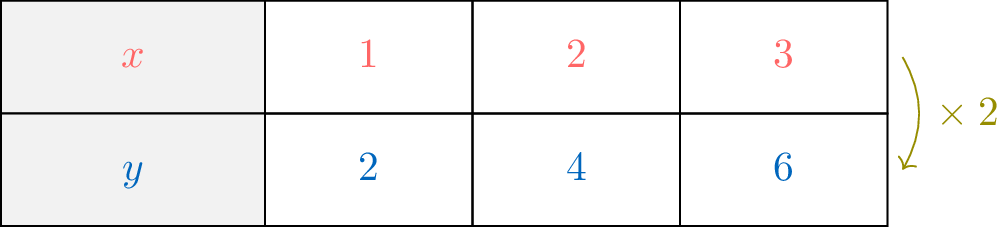
\(\textcolor{colorprop}{2} = \textcolor{olive}{2} \times \textcolor{colordef}{1},\quad \textcolor{colorprop}{4} = \textcolor{olive}{2} \times \textcolor{colordef}{2},\quad \textcolor{colorprop}{6} = \textcolor{olive}{2} \times \textcolor{colordef}{3}\)

\(\textcolor{colorprop}{2} = \textcolor{olive}{2} \times \textcolor{colordef}{1},\quad \textcolor{colorprop}{4} = \textcolor{olive}{2} \times \textcolor{colordef}{2},\quad \textcolor{colorprop}{6} = \textcolor{olive}{2} \times \textcolor{colordef}{3}\)
Methods for Calculating a Fourth Proportional
Method Calculating a Fourth Proportional
For her birthday, Su invites her friends to the cinema. She was supposed to pay \(\textcolor{colorprop}{28}\) dollars for \(\textcolor{colordef}{4}\) tickets. Eventually, Su's parents decide to join and offer to pay.
Knowing that the price is proportional to the number of tickets, how much will Su's parents pay for \(\textcolor{colordef}{6}\) tickets?
Knowing that the price is proportional to the number of tickets, how much will Su's parents pay for \(\textcolor{colordef}{6}\) tickets?
- Method 1: Coefficient of Proportionality
- The coefficient of proportionality is:$$\begin{aligned}\textcolor{olive}{\text{Coefficient}}&= \dfrac{\textcolor{colorprop}{\text{Price}}}{\textcolor{colordef}{\text{Number of Tickets}}} \\&= \dfrac{\textcolor{colorprop}{28}}{\textcolor{colordef}{4}} \\&= \textcolor{olive}{7}\end{aligned}$$
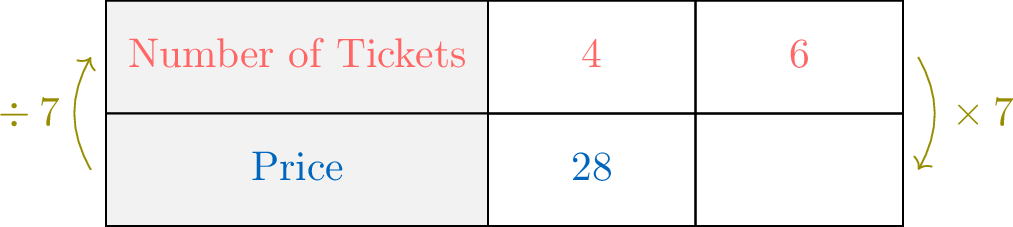
- For \(\textcolor{colordef}{6}\) tickets, the price is:$$\begin{aligned}\textcolor{colorprop}{\text{Price}} &=\textcolor{olive}{\text{Coefficient}}\times \textcolor{colordef}{\text{Number of Tickets}}\\&=\textcolor{olive}{7} \times \textcolor{colordef}{6} \\&= \textcolor{colorprop}{42\text{ dollars per ticket}}\end{aligned}$$Therefore, \(\textcolor{colordef}{6}\) tickets cost \(\textcolor{colorprop}{42}\) dollars.
- The coefficient of proportionality is:$$\begin{aligned}\textcolor{olive}{\text{Coefficient}}&= \dfrac{\textcolor{colorprop}{\text{Price}}}{\textcolor{colordef}{\text{Number of Tickets}}} \\&= \dfrac{\textcolor{colorprop}{28}}{\textcolor{colordef}{4}} \\&= \textcolor{olive}{7}\end{aligned}$$
- Method 2: Cross Multiplication in a Proportional Table
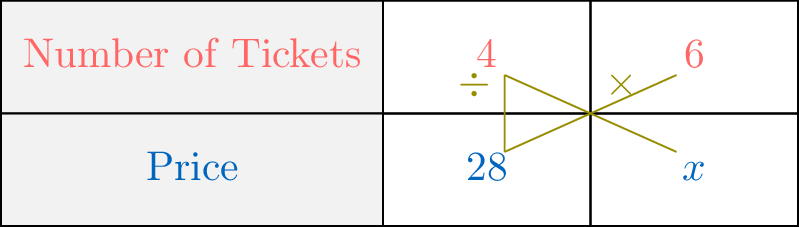
- Method 3: Unit Rate with Equivalent Ratios
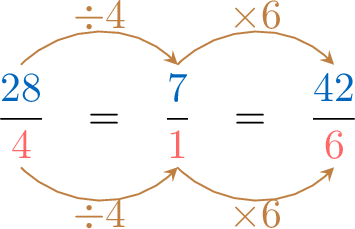
- Method 4: Proportion Equation$$\begin{aligned}\dfrac{\textcolor{colorprop}{28}}{\textcolor{colordef}{4}} &= \dfrac{\textcolor{colorprop}{x}}{\textcolor{colordef}{6}} \\\textcolor{colordef}{4} \times \textcolor{colorprop}{x} &= \textcolor{colorprop}{28} \times \textcolor{colordef}{6} && \text{(cross multiplication)} \\\textcolor{colorprop}{x} &= \dfrac{\textcolor{colorprop}{28} \times \textcolor{colordef}{6}}{\textcolor{colordef}{4}} \\\textcolor{colorprop}{x} &= \textcolor{colorprop}{42}\end{aligned}$$Therefore, \(\textcolor{colordef}{6}\) tickets cost \(\textcolor{colorprop}{42}\) dollars.
- Method 5: Unit Rate in Words
- \(\textcolor{colordef}{4}\) tickets cost \(\textcolor{colorprop}{28}\) dollars, so \(\textcolor{colordef}{1}\) ticket costs \(\textcolor{colorprop}{28} \div \textcolor{colordef}{4} = \textcolor{olive}{7}\) dollars.
- \(\textcolor{colordef}{6}\) tickets cost \( \textcolor{olive}{7} \times\textcolor{colordef}{6} = \textcolor{colorprop}{42}\) dollars.