Fractions
Definitions
Definition Fraction
A fraction consists of two numbers: the numerator, \(a\), and the denominator, \(b \neq 0\), separated by a horizontal bar: 
A fraction can be represented as:
- Symbol : \(\dfrac{2}{3}\)
- Words : two thirds or two over three
- Linear model :

Fraction as Quotient
Two cakes are shared equally among three people. 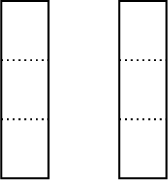
- Use the figure to determine what fraction of the cakes each person receives.
- Copy and complete: \(\ldots\) cakes \(\div\) \(\ldots\) people \(= \dfrac{\ldots}{\ldots}\) of a cake each.
- Each cake is divided into three equal parts. Each person receives one piece from each cake, totaling two pieces. Since each cake is divided into three parts, each piece represents \(\dfrac{1}{3}\) of a cake. Therefore, each person receives:\[\frac{1}{3} + \frac{1}{3} = \frac{2}{3} \text{ of the cakes.}\]

- \(2\) cakes \(\div\) \(3\) people \(= \dfrac{2}{3}\) of a cake each.
Proposition Fraction as Quotient
A fraction is a quotient that represents the result of division. It tells us how much of something we have when we divide it into equal parts.
- The top number (numerator) is the whole.
- The bottom number (denominator) is the number of equal parts the whole is divided into.
Example
On the number line
Method Representing a Fraction on the Number Line
To represent the fraction \(\dfrac{\textcolor{colordef}{2}}{\textcolor{colorprop}{3}}\) on a number line.
- Draw a straight line and mark the points 0 and 1.

- Divide the line between 0 and 1 into \(\textcolor{colorprop}{3}\) equal parts.

- Count \(\textcolor{colordef}{2}\) parts from 0 and mark the point.

Equivalent Fractions
Definition Equivalent Fractions
- When you multiply the numerator and the denominator by the same number, the fractions are equals.
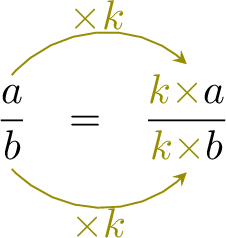
- When you divide the numerator and the denominator by the same number, the fractions are equals.
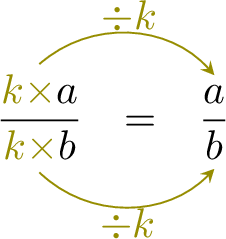
Example
Example
Simplification
Louis eats \( \dfrac{6}{12} \) of a pizza. Hugo says, "Hey, \( \dfrac{6}{12} \) is the same as \( \dfrac{1}{2} \). It's easier to understand if you simplify the fraction!".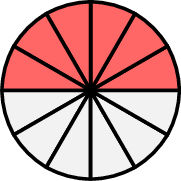 \(=\)
\(=\) 
 \(=\)
\(=\) 
- Louis: "How is \( \dfrac{1}{2} \) easier?"
- Hugo: "Because \( \dfrac{1}{2} \) is the simplified form of \( \dfrac{6}{12} \). It means you ate 1 out of 2 slices instead of 6 out of 12 slices. It’s the same amount of pizza, but it’s simpler to understand!"
Definition Simplest form
A fraction is in simplest form if it is written with the smallest possible whole number numerator and denominator, that is, if its numerator and denominator have no common factors other than 1.
Example
- \(\frac{2}{3}\) is in simplest form.
- \(\frac{4}{6}\) is not in simplest form because we can write \(\frac{4}{6}=\frac{2}{3}\).
Method Simplifying a fraction
To simplify a fraction (or to write a fraction in its simplest form), we cancel the greatest common factor of the numerator and the denominator .
Example
Simplify \(\dfrac{4}{6}\).
$$\begin{aligned}[t]\dfrac{4}{6} &= \dfrac{2 \times \textcolor{olive}{\cancel{2}}}{3 \times \textcolor{olive}{\cancel{2}}} \\ &= \dfrac{2}{3}\end{aligned}$$
Cross Multiplication
We have learned that two fractions are equal if we can multiply both the numerator and the denominator by the same number.
For example:$$\dfrac{2}{3} = \dfrac{\textcolor{olive}{5} \times 2}{\textcolor{olive}{5} \times 3} = \dfrac{10}{15}$$Now, let's explore another way to check if two fractions are equal.
We can investigate the relationship between their numerators and denominators:$$\begin{aligned}2 \times 15 &= 2 \times (\textcolor{olive}{5} \times 3) \\&= \textcolor{olive}{5} \times 2 \times 3 \\&= 10 \times 3\end{aligned}$$So, we can see that:$$2 \times 15 = 3 \times 10$$This leads us to a new way of checking if two fractions are equal: by cross multiplying and comparing the products.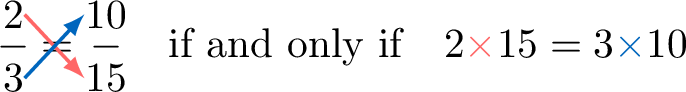
For example:$$\dfrac{2}{3} = \dfrac{\textcolor{olive}{5} \times 2}{\textcolor{olive}{5} \times 3} = \dfrac{10}{15}$$Now, let's explore another way to check if two fractions are equal.
We can investigate the relationship between their numerators and denominators:$$\begin{aligned}2 \times 15 &= 2 \times (\textcolor{olive}{5} \times 3) \\&= \textcolor{olive}{5} \times 2 \times 3 \\&= 10 \times 3\end{aligned}$$So, we can see that:$$2 \times 15 = 3 \times 10$$This leads us to a new way of checking if two fractions are equal: by cross multiplying and comparing the products.
Proposition Cross Multiplication Property
Example
Solve \(x\) for \(\dfrac{10}{5}=\dfrac{x}{8}\).
Addition and Subtraction
Definition Addition and Subtraction of Fractions with Common Denominators
- When we add fractions with common denominators, we keep the denominator the same and add the numerators:$$\dfrac{a}{b} + \dfrac{c}{b} = \dfrac{a + c}{b}$$
- When we subtract fractions with common denominators, we keep the denominator the same and subtract the numerators:$$\dfrac{a}{b} - \dfrac{c}{b} = \dfrac{a - c}{b}$$
Example
Calculate \(\dfrac{1}{4} + \dfrac{2}{4}\).
- $$\begin{aligned}[t]\dfrac{1}{4} + \dfrac{2}{4} &= \dfrac{1 + 2}{4} \\&= \dfrac{3}{4}\end{aligned}$$
 \(+\)
\(+\)  \(=\)
\(=\) 
Method Addition or Subtraction of Fractions with Different Denominators
To add or subtract fractions with different denominators:
- Find a common denominator: Choose a common multiple of the denominators.
- Convert each fraction: Rewrite each fraction so it has the common denominator.
- Add or subtract the numerators: Add or subtract the numerators and keep the denominator the same.
Example
Calculate \(\dfrac{3}{4} + \dfrac{5}{6}\).
- Find a common denominator:To add fractions, they must have the same denominator.
- Multiples of 4: 4, 8, 12, 16, 20, \(\dots\)
- Multiples of 6: 6, 12, 18, 24, \(\dots\)
- The smallest common denominator is 12.
- \(\begin{aligned}[t]\dfrac{3}{4}+\dfrac{5}{6}&= \frac{3 \times \textcolor{olive}{3}}{4 \times \textcolor{olive}{3}}+\frac{5 \times \textcolor{olive}{2}}{6 \times \textcolor{olive}{2}}&&\\&=\dfrac{9}{12}+\dfrac{10}{12}&&\quad\text{(common denominator}= 12)\\&=\dfrac{9+10}{12}&&\quad\text{(adding numerators)}\\&=\dfrac{19}{12}&&\\\end{aligned}\)
- Visual representation:
 \(+\)
\(+\)
\(=\)  \(+\)
\(+\)
\(=\) 
Multiplication of a Fraction by a Number
Hugo has a cake. He eats \(\dfrac{1}{4}\) of the cake each day.
How much of the cake will he have eaten after 3 days?
How much of the cake will he have eaten after 3 days?
After 3 days, Hugo will have eaten:
| \(3\times\) | \(=\) | |
| \(=\) |
Definition Multiplication of a Fraction by a Number
To multiply a fraction by a whole number:
- Multiply the numerator by the number.
- Keep the denominator the same.
Example
Calculate \(3 \times \dfrac{2}{5}\).
- Mathematical calculation:$$\begin{aligned}[t]3 \times \dfrac{2}{5} &= \dfrac{3 \times 2}{5} \\&= \dfrac{6}{5}\end{aligned}$$
- Visual representation:
\(3\times\) 
\(=\)  \(+\)
\(+\)  \(+\)
\(+\) 
\(=\)
Multiplication of Fractions
Find the area of the shaded rectangle that has sides of length \(\textcolor{colordef}{\dfrac{2}{3}}\) and \(\textcolor{colorprop}{\dfrac{1}{2}}\). 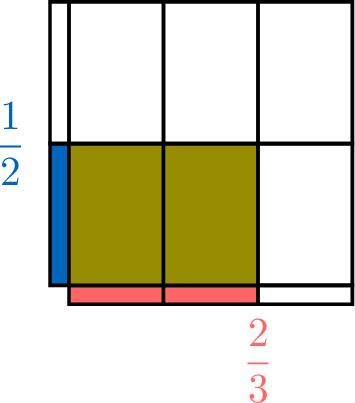
- The unit rectangle is divided into \(\textcolor{colordef}{3}\) columns and \(\textcolor{colorprop}{2}\) rows, giving a total of \(3 \times 2 = 6\) equal parts.
- The shaded rectangle covers \(\textcolor{colordef}{2}\) columns and \(\textcolor{colorprop}{1}\) row, so it covers \(2 \times 1 = \textcolor{olive}{2}\) parts.
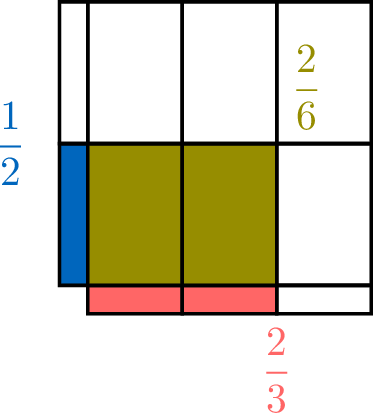
- Therefore, the area of the shaded rectangle is \(\textcolor{olive}{\dfrac{2}{6}}\).
- As the product of the side lengths gives the area of a rectangle, we have: $$\begin{aligned}[t] \textcolor{colordef}{\dfrac{2}{3}} \times \textcolor{colorprop}{\dfrac{1}{2}} &= \dfrac{\textcolor{colordef}{2} \times \textcolor{colorprop}{1}}{\textcolor{colordef}{3} \times \textcolor{colorprop}{2}} \\ &= \textcolor{olive}{\dfrac{2}{6}} \end{aligned}$$
Definition Multiplication of Fractions
To multiply fractions, tu multiplies the numerators and tu multiplies the denominators:$$\textcolor{colordef}{\dfrac{a}{b}} \times \textcolor{colorprop}{\dfrac{c}{d}}= \dfrac{\textcolor{colordef}{a} \times \textcolor{colorprop}{c}}{\textcolor{colordef}{b} \times \textcolor{colorprop}{d}}$$
Example
Calculate \( \dfrac{5}{2} \times \dfrac{3}{4}\).
$$\begin{aligned}[t]\dfrac{5}{2} \times \dfrac{3}{4}&= \dfrac{5 \times 3}{2 \times 4} \\&= \dfrac{15}{8}\end{aligned}$$
Method Canceling Common Factors
To make multiplication easier, tu peux annuler any common factors in the numerators and denominators before multiplying.
Example
Calculate \(\dfrac{31}{7} \times \dfrac{12}{31}\).
$$\begin{aligned}[t]\dfrac{31}{7} \times \dfrac{12}{31}&= \dfrac{\textcolor{colordef}{\cancel{31}} \times 12}{7 \times \textcolor{colordef}{\cancel{31}}}&& \text{(cancel the common factor 31)} \\&= \dfrac{12}{7}\end{aligned}$$
Division of Fractions
Definition Reciprocal
The reciprocal of a number is a number that, when multiplied by the original number, gives 1.
Proposition Reciprocal of a fraction
The reciprocal of the fraction \(\dfrac{a}{b}\) is \(\dfrac{b}{a}\).
$$\begin{aligned}[t]\dfrac{a}{b}\times \dfrac{b}{a} &= \dfrac{a\times b}{b\times a} && \text{(les produits sont identiques)}\\ &= \dfrac{1}{1} &&\\ &= 1\,.\end{aligned}$$
Example
State the reciprocal of \(\dfrac{5}{7}\).
The reciprocal of \(\dfrac{5}{7}\) is \(\dfrac{7}{5}\).
Definition Division of fractions
To divide by a fraction, you multiply by its reciprocal:$$\dfrac{a}{b}\div \dfrac{c}{d}=\dfrac{a}{b}\times \dfrac{d}{c}\,,$$or equivalently,$$\dfrac{\frac{a}{b}}{\frac{c}{d}}=\dfrac{a}{b}\times \dfrac{d}{c}\,.$$
Example
Calculate \(\dfrac{2}{3}\div \dfrac{5}{7}\).
$$\begin{aligned}[t]\dfrac{2}{3}\div \dfrac{5}{7} &= \dfrac{2}{3}\times \dfrac{7}{5} && \text{(multiply by the reciprocal)}\\ &= \dfrac{2\times 7}{3\times 5} && \text{(multiply numerators and denominators)}\\ &= \dfrac{14}{15}\,.\end{aligned}$$
Sign rules
Recall from the chapter on negative numbers that dividing a positive by a negative, or a negative by a positive, yields a negative result.
Since the fraction bar represents division, consider the fraction$$\frac{-3}{2}=\overbrace{(-3)}^{\text{negative}} \div \overbrace{2}^{\text{positive}}=\overbrace{-\left(3\div 2\right)}^{\text{negative}}=-\frac{3}{2}\,.$$Similarly,$$\frac{3}{-2}=\overbrace{3}^{\text{positive}} \div \overbrace{(-2)}^{\text{negative}}=\overbrace{-\left(3\div 2\right)}^{\text{negative}}=-\frac{3}{2}\,.$$So, in general:
Since the fraction bar represents division, consider the fraction$$\frac{-3}{2}=\overbrace{(-3)}^{\text{negative}} \div \overbrace{2}^{\text{positive}}=\overbrace{-\left(3\div 2\right)}^{\text{negative}}=-\frac{3}{2}\,.$$Similarly,$$\frac{3}{-2}=\overbrace{3}^{\text{positive}} \div \overbrace{(-2)}^{\text{negative}}=\overbrace{-\left(3\div 2\right)}^{\text{negative}}=-\frac{3}{2}\,.$$So, in general:
Proposition Sign rules
$$\dfrac{-a}{b}=\dfrac{a}{-b}=-\dfrac{a}{b}\,,$$and$$\dfrac{-a}{-b}=\dfrac{a}{b}\,.$$
Example
Simplify \(\dfrac{-4}{-6}\).
$$\begin{aligned}[t]\dfrac{-4}{-6} &= \dfrac{4}{6} \quad &\text{(a negative divided by a negative is positive)}\\ &= \dfrac{2\times\textcolor{olive}{2}}{3\times\textcolor{olive}{2}} \quad &\text{(cancel the common factor 2)}\\ &= \dfrac{2}{3}\,.\end{aligned}$$
Order of Operations
Definition Order of Operations
The division line in a fraction acts as a grouping symbol (like parentheses). This means that, according to the order of operations (PEMDAS), you must first evaluate the numerator and the denominator before performing the division.
Example
Simplify \(\frac{1+7}{3\times 4}\).
$$\begin{aligned}[t]\frac{1+7}{3\times 4}&=\frac{8}{12}&&\text{(evaluate numerator and denominator)}\\&=\frac{2\times \textcolor{olive}{\cancel{4}}}{3\times \textcolor{olive}{\cancel{4}}}&& \text{(cancel common factor)}\\&=\frac{2}{3}\\\end{aligned}$$