Fractions
Definitions
Hugo is very hungry after playing soccer. His dad baked two identical cakes.
Hugo eats one whole cake:

Hugo eats one whole cake:
- Hugo eats one whole cake and half of another cake.

- The numerator (top number) shows how many parts Hugo eats: \(3\).
- The denominator (bottom number) shows how many equal parts make one cake: \(2\).
- So Hugo eats \(\dfrac{3}{2}\) cakes in total.
Definition Fraction
A fraction includes two numbers: the numerator and the denominator, separated by a bar. 

On the number line
- Hugo is walking along a path.

- He stops and asks himself, "Where am I?"
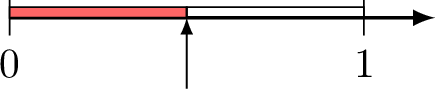
- His father says, "You are at half of the way that is \(\dfrac{1}{2}\)."
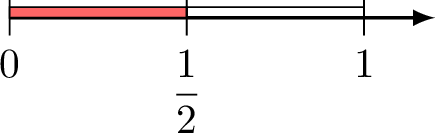
Method Representing a Fraction on the Number Line
To represent the fraction \(\dfrac{\textcolor{colordef}{2}}{\textcolor{colorprop}{3}}\) on a number line.
- Draw a straight line and mark the points 0 and 1.

- Divide the line between 0 and 1 into \(\textcolor{colorprop}{3}\) equal parts.

- Count \(\textcolor{colordef}{2}\) parts from 0 and mark the point.

Equivalent Fractions
Mr. Tariel has a cake that he cuts into 3 equal parts. He plans to give 1 part to his son, Louis.
His dad replies, "Alright," and cuts each of the 3 parts in half, making 6 smaller equal parts. He then gives Louis 2 of these smaller pieces.
Why is Louis still not happy?
His dad replies, "Alright," and cuts each of the 3 parts in half, making 6 smaller equal parts. He then gives Louis 2 of these smaller pieces.
Why is Louis still not happy?
Even though Louis got 2 pieces instead of 1, the total amount of cake he received is the same as before. His dad just cut the cake into smaller pieces. \(\quad =\quad \)
\(\quad =\quad \)
Definition Equivalent Fractions
- When you multiply the numerator and the denominator by the same number, the fractions are equals.

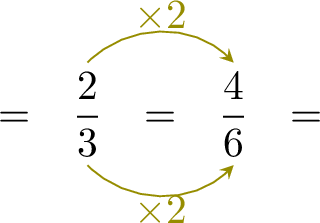

- When you divide the numerator and the denominator by the same number, the fractions are equals.

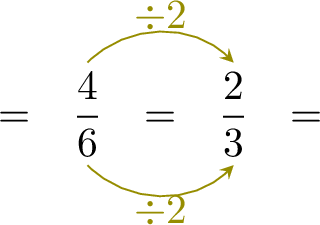

Simplification
Louis eats \( \dfrac{6}{12} \) of a pizza. Hugo says, "Hey, \( \dfrac{6}{12} \) is the same as \( \dfrac{1}{2} \). It's easier to understand if you simplify the fraction!".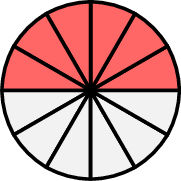 \(=\)
\(=\) 
 \(=\)
\(=\) 
- Louis: "How is \( \dfrac{1}{2} \) easier?"
- Hugo: "Because \( \dfrac{1}{2} \) is the simplified form of \( \dfrac{6}{12} \). It means you ate 1 out of 2 slices instead of 6 out of 12 slices. It’s the same amount of pizza, but it’s simpler to understand!"
Method Simplifying a fraction
To simplify a fraction, we find an equivalent fraction with the smallest possible numerator and denominator.
Example
Simplify \(\dfrac{4}{6}\)
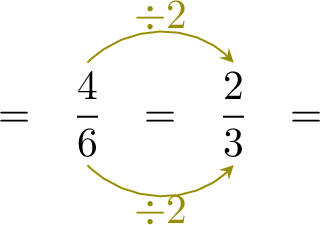
Cross Multiplication
We have learned that two fractions are equal if we can multiply both the numerator and the denominator by the same number.
For example:$$\dfrac{2}{3} = \dfrac{\textcolor{olive}{5} \times 2}{\textcolor{olive}{5} \times 3} = \dfrac{10}{15}$$Now, let's explore another way to check if two fractions are equal.
We can investigate the relationship between their numerators and denominators:$$\begin{aligned}2 \times 15 &= 2 \times (\textcolor{olive}{5} \times 3) \\&= \textcolor{olive}{5} \times 2 \times 3 \\&= 10 \times 3\end{aligned}$$So, we can see that:$$2 \times 15 = 3 \times 10$$This leads us to a new way of checking if two fractions are equal: by cross multiplying and comparing the products.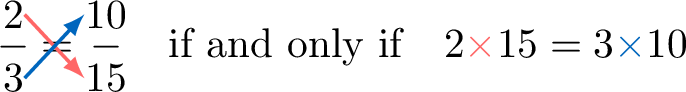
For example:$$\dfrac{2}{3} = \dfrac{\textcolor{olive}{5} \times 2}{\textcolor{olive}{5} \times 3} = \dfrac{10}{15}$$Now, let's explore another way to check if two fractions are equal.
We can investigate the relationship between their numerators and denominators:$$\begin{aligned}2 \times 15 &= 2 \times (\textcolor{olive}{5} \times 3) \\&= \textcolor{olive}{5} \times 2 \times 3 \\&= 10 \times 3\end{aligned}$$So, we can see that:$$2 \times 15 = 3 \times 10$$This leads us to a new way of checking if two fractions are equal: by cross multiplying and comparing the products.
Proposition Cross Multiplication Property
Example
Solve \(x\) for \(\dfrac{10}{5}=\dfrac{x}{8}\).
Ordering Fractions
- Hugo eats \(\dfrac{3}{4}\) of a cake.

- Louis eats \(\dfrac{5}{8}\) of the same cake.

- We need to compare the fractions \(\dfrac{3}{4}\) and \(\dfrac{5}{8}\).
- To compare fractions, the pieces must be the same size. We do this by finding a common denominator.
- Convert \(\dfrac{3}{4}\) to an equivalent fraction with denominator 8:
 \quad
\quad 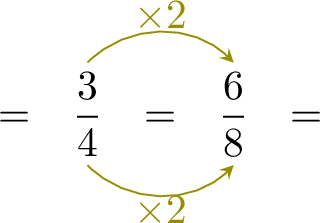 \quad
\quad 
- Now, Hugo eats \(\dfrac{6}{8}\) of the cake and Louis eats \(\dfrac{5}{8}\).
- Since \(\dfrac{6}{8} > \dfrac{5}{8}\), Hugo eats more cake.
Definition Ordering Fractions with the Same Denominator
For two fractions with the same denominator, the fraction with the larger numerator is larger.
Example
Compare \(\dfrac{3}{4}\) and \(\dfrac{2}{4}\).
Method Comparing Fractions with Different Denominators
To compare two fractions with different denominators:
- Find a common denominator.
- Convert each fraction to an equivalent fraction with that denominator.
- Compare the numerators.
Example
Compare \(\dfrac{1}{2}\) and \(\dfrac{3}{4}\).
- Since \(\dfrac{1}{2}\) and \(\dfrac{3}{4}\) have different denominators, we change \(\dfrac{1}{2}\) into an equivalent fraction with denominator 4:
 \quad
\quad 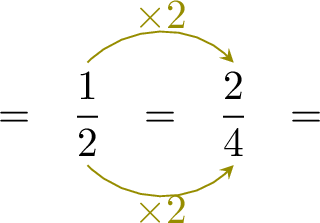 \quad
\quad 
- Compare the numerators: \[\dfrac{2}{4} < \dfrac{3}{4}\]
- Therefore, \[\dfrac{1}{2} < \dfrac{3}{4}\]
- In pictures:
 \quad = \quad
\quad = \quad  \quad < \quad
\quad < \quad 
Addition and Subtraction with Common Denominators
Hugo eats \(\dfrac{2}{4}\) of a cake:  and Louis eats \(\dfrac{1}{4}\) of the same cake:
and Louis eats \(\dfrac{1}{4}\) of the same cake: 
Which fraction of the cake have Hugo and Louis eaten together?
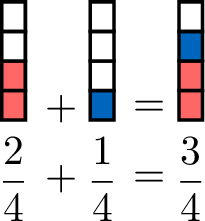

Which fraction of the cake have Hugo and Louis eaten together?
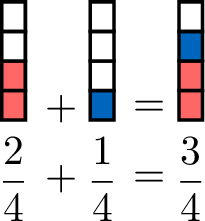
Definition Addition of Fractions with Common Denominators
When we add fractions with common denominators, we keep the denominator the same and add the numerators: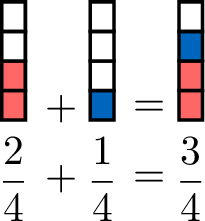
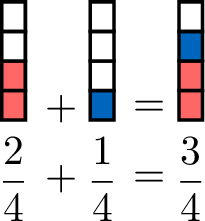
Definition Subtraction of Fractions with Common Denominators
When we subtract fractions with common denominators, we keep the denominator the same and subtract the numerators: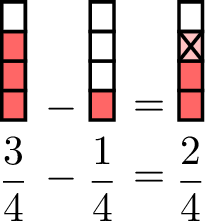
Addition and Subtraction with Different Denominators
Hugo eats \(\dfrac{1}{2}\) of a cake:  and Louis eats \(\dfrac{1}{4}\) of the same cake:
and Louis eats \(\dfrac{1}{4}\) of the same cake:  .
.
What fraction of the cake have Hugo and Louis eaten together?
What fraction of the cake have Hugo and Louis eaten together?
- Step 1: Find a common denominator: To add the fractions, we need equal-sized parts. Divide each of Hugo's parts into two smaller parts:
 \quad \(=\) \quad
\quad \(=\) \quad
- Step 2: Add the fractions using the common denominator: Now, we can add the two fractions:
 \(+\)
\(+\) 
\(=\)  \(+\)
\(+\) 
\(=\) 
\(\dfrac{1}{2}+\dfrac{1}{4}\) \(=\) \(\dfrac{2}{4}+\dfrac{1}{4}\) \(=\) \(\dfrac{3}{4}\) - Step 3: Final Answer: Hugo and Louis eat \(\dfrac{3}{4}\) of the cake together:

Method Addition or Subtraction of Fractions with Different Denominators
To add or subtract fractions with different denominators:
- Find a common denominator: Choose a common multiple of the denominators.
- Convert each fraction: Rewrite each fraction so it has the common denominator.
- Add or subtract the numerators: Add or subtract the numerators and keep the denominator the same.
Example
Calculate \(\dfrac{3}{4} + \dfrac{5}{6}\).
- Find a common denominator:To add fractions, they must have the same denominator.
- Multiples of 4: 4, 8, 12, 16, 20, \(\dots\)
- Multiples of 6: 6, 12, 18, 24, \(\dots\)
- The smallest common denominator is 12.
- \(\begin{aligned}[t]\dfrac{3}{4}+\dfrac{5}{6}&= \frac{3 \times \textcolor{olive}{3}}{4 \times \textcolor{olive}{3}}+\frac{5 \times \textcolor{olive}{2}}{6 \times \textcolor{olive}{2}}&&\\&=\dfrac{9}{12}+\dfrac{10}{12}&&\quad\text{(common denominator}= 12)\\&=\dfrac{9+10}{12}&&\quad\text{(adding numerators)}\\&=\dfrac{19}{12}&&\\\end{aligned}\)
- Visual representation:
 \(+\)
\(+\)
\(=\)  \(+\)
\(+\)
\(=\) 
Fraction as Quotient
Two cakes are shared equally among three people. 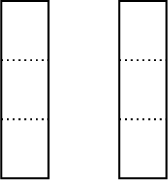
- Use the figure to determine what fraction of the cakes each person receives.
- Copy and complete: \(\ldots\) cakes \(\div\) \(\ldots\) people \(= \dfrac{\ldots}{\ldots}\) of a cake each.
- Each cake is divided into three equal parts. Each person receives one piece from each cake, totaling two pieces. Since each cake is divided into three parts, each piece represents \(\dfrac{1}{3}\) of a cake. Therefore, each person receives:\[\frac{1}{3} + \frac{1}{3} = \frac{2}{3} \text{ of the cakes.}\]

- \(2\) cakes \(\div\) \(3\) people \(= \dfrac{2}{3}\) of a cake each.
Proposition Fraction as Quotient
A fraction is a quotient that represents the result of division. It tells us how much of something we have when we divide it into equal parts. 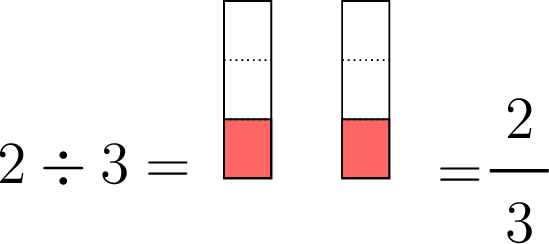
The fraction \(\dfrac{2}{3}\) is the number which, when multiplied by \(3\), gives \(2\):$$\dfrac{2}{3}\times 3 = 2 $$
- The top number (numerator) is the whole.
- The bottom number (denominator) is the number of equal parts the whole is divided into.
Fraction as Ratio
In a class of 30 students, \(\dfrac{2}{3}\) of the students are girls. How many students are girls?
The fraction \(\dfrac{2}{3}\) represents the ratio of girls to the total number of students.
We can visualize this problem using a bar model: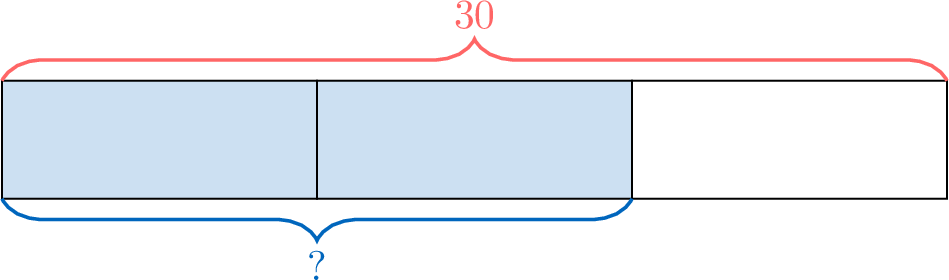
We can visualize this problem using a bar model:
- Method 1 (unitary method):
- Divide the total number of students by the denominator of the fraction to find how many students are in each part:
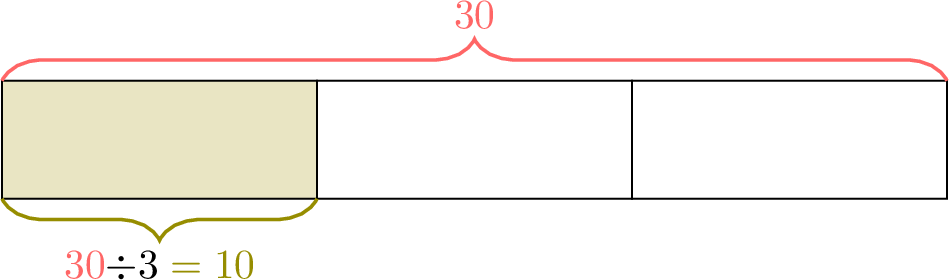
- Multiply the result by the numerator to find how many students are girls:
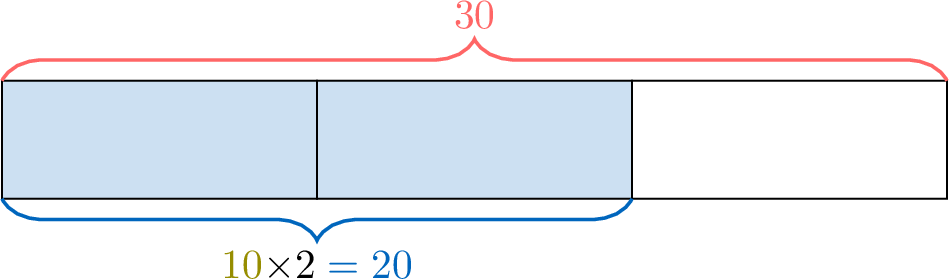
- Divide the total number of students by the denominator of the fraction to find how many students are in each part:
- Method 2 (calculation using a formula): $$ \begin{aligned}[t] \textcolor{colorprop}{\text{Number of girls}} &=\dfrac{2}{3} \text{ of } \textcolor{colordef}{30} \\ &= \dfrac{2}{3} \times \textcolor{colordef}{30} \\ &= \left( 2 \div 3 \right) \times \textcolor{colordef}{30} \\ &= \textcolor{colorprop}{20} \end{aligned} $$
Definition Fractions as Ratios
A fraction can represent the ratio of part to the whole:$$\dfrac{\text{Part}}{\text{Whole}}$$
Example
There are 3 apples in Hugo's basket. 2 of the apples are red.
Method Finding a Quantity from a Fraction (Ratio)
To calculate \(\dfrac{2}{3}\) of \(\textcolor{colordef}{30}\):
- Method 1 (unitary method):
- Divide the total by the denominator to find the amount for one part:
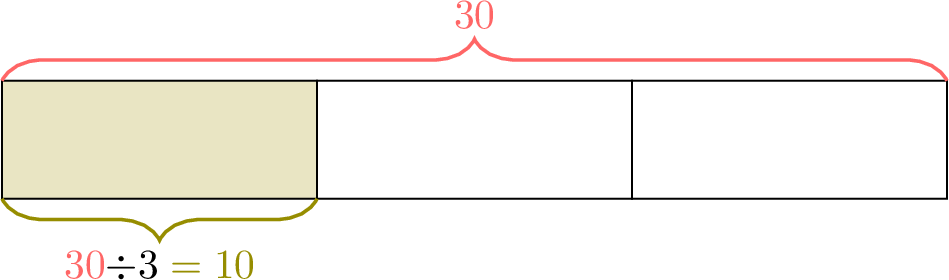
- Multiply the result by the numerator to find the desired quantity:
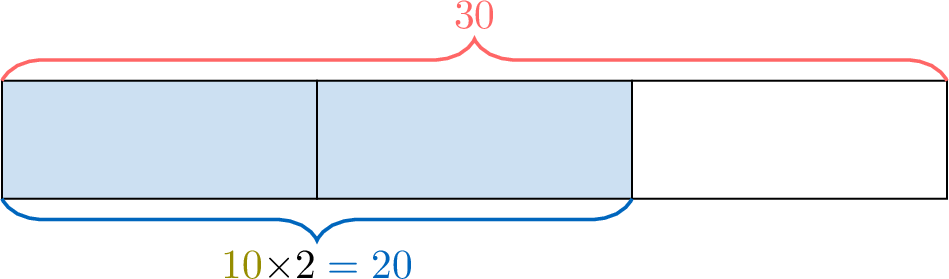
- Divide the total by the denominator to find the amount for one part:
- Method 2 (calculation using a formula): $$ \begin{aligned}[t]\dfrac{2}{3} \text{ of } \textcolor{colordef}{30} &= \dfrac{2}{3} \times \textcolor{colordef}{30} \\ &= \left( 2 \div 3 \right) \times \textcolor{colordef}{30} \\ &= \textcolor{colorprop}{20} \end{aligned} $$
Fraction as Decimal Number
Decimals and fractions can both be used to describe values between whole numbers. We can convert:
- Fraction into Decimal: Perform the division of the numerator by the denominator. For example, $$ \begin{aligned}[t] \frac{1}{2} &= 1 \div 2 \\ &= 0.5 \end{aligned} $$
- Decimal into Fraction: Multiply the decimal by a power of 10 (10, 100, 1000, \(\dots\)) to eliminate the decimal point. Then, write the result over the same power of 10 to form a fraction. For example: $$ \begin{aligned}[t] 1.3 &= \frac{1.3 \times 10}{10} \\ &= \frac{13}{10} \end{aligned} $$
Method Converting a Fraction to a Decimal
- Division Method: Perform the division of the numerator by the denominator.
- Power of 10 Denominator Method: Find an equivalent fraction where the denominator is a power of 10.
Example
Convert \(\dfrac{3}{4}\) to a decimal number.
- Division Method: $$ \begin{aligned}[t] \frac{3}{4} &= 3 \div 4 \\ &= 0.75 \end{aligned} $$
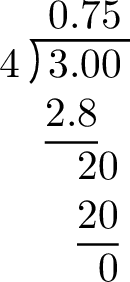
- Power of 10 Denominator Method: $$ \begin{aligned}[t] \frac{3}{4} &= \frac{3 \textcolor{olive}{\times 25}}{4 \textcolor{olive}{\times 25}} \\ &= \frac{75}{100} \\ &= 75\div 100 \\ &= 0.75 \end{aligned} $$
Method Converting Decimal to Fraction
- Multiply the decimal by a power of 10 (10, 100, 1000, \(\dots\)) to eliminate the decimal point.
- Write the result over the same power of 10 to form a fraction.
Example
Convert \(1.3\) to a fraction.
$$ \begin{aligned}[t] 1.3 &= \frac{1.3 \times 10}{10} \\ &= \frac{13}{10} \end{aligned} $$
Proper and Improper Fractions
You have \(\dfrac{5}{2}\) of a pain au chocolat:  .
.
How can you represent this amount in simple way?
How can you represent this amount in simple way?
You have 2 whole pains au chocolat and \(\dfrac{1}{2}\) of another pain au chocolat. Is it easier to think of \(\dfrac{5}{2}\) as \(2+\dfrac{1}{2}\)? This is the concept of a mixed number.
Definition Proper and improper fractions
A fraction which has numerator less than its denominator is called a proper fraction.
A fraction which has numerator greater than its denominator is called an improper fraction.
A fraction which has numerator greater than its denominator is called an improper fraction.
Example
- \(\dfrac{2}{3}=\)
 is a proper fraction.
is a proper fraction. - \(\dfrac{5}{3}=1+\dfrac{2}{3}=\)
 is an improper fraction.
is an improper fraction.
Definition Mixed Number
A mixed number is a representation of a number that combines a whole number and a proper fraction.
By standard convention, the addition symbol is implied and thus not explicitly written:\(1\dfrac{2}{3} \text{ is understood as } 1 + \dfrac{2}{3} =\) 
By standard convention, the addition symbol is implied and thus not explicitly written: