Fractions
Definitions
Hugo is very hungry after playing soccer. His dad baked two identical cakes.
Hugo eats one whole cake:

Hugo eats one whole cake:
- Hugo eats one whole cake and half of another cake.

- The numerator (top number) shows how many parts Hugo eats: \(3\).
- The denominator (bottom number) shows how many equal parts make one cake: \(2\).
- So Hugo eats \(\dfrac{3}{2}\) cakes in total.
Definition Fraction
A fraction includes two numbers: the numerator and the denominator, separated by a bar. 

On the number line
- Hugo is walking along a path.

- He stops and asks himself, "Where am I?"
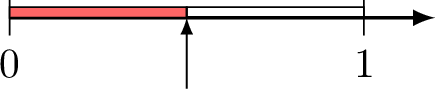
- His father says, "You are at half of the way that is \(\dfrac{1}{2}\)."
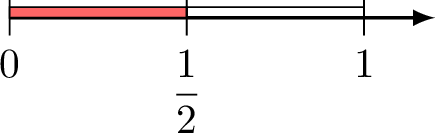
Method Representing a Fraction on the Number Line
To represent the fraction \(\dfrac{\textcolor{colordef}{2}}{\textcolor{colorprop}{3}}\) on a number line.
- Draw a straight line and mark the points 0 and 1.

- Divide the line between 0 and 1 into \(\textcolor{colorprop}{3}\) equal parts.

- Count \(\textcolor{colordef}{2}\) parts from 0 and mark the point.

Equivalent Fractions
Mr. Tariel has a cake that he cuts into 3 equal parts. He plans to give 1 part to his son, Louis.
His dad replies, "Alright," and cuts each of the 3 parts in half, making 6 smaller equal parts. He then gives Louis 2 of these smaller pieces.
Why is Louis still not happy?
His dad replies, "Alright," and cuts each of the 3 parts in half, making 6 smaller equal parts. He then gives Louis 2 of these smaller pieces.
Why is Louis still not happy?
Even though Louis got 2 pieces instead of 1, the total amount of cake he received is the same as before. His dad just cut the cake into smaller pieces. \(\quad =\quad \)
\(\quad =\quad \)
Definition Equivalent Fractions
- When you multiply the numerator and the denominator by the same number, the fractions are equals.

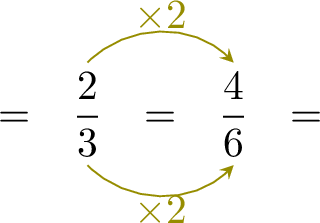

- When you divide the numerator and the denominator by the same number, the fractions are equals.

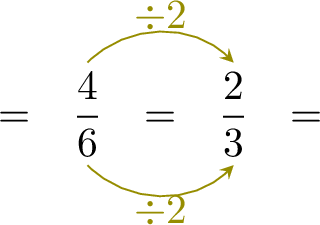

Simplification
Louis eats \( \dfrac{6}{12} \) of a pizza. Hugo says, "Hey, \( \dfrac{6}{12} \) is the same as \( \dfrac{1}{2} \). It's easier to understand if you simplify the fraction!".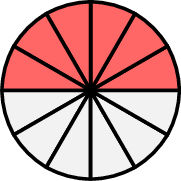 \(=\)
\(=\) 
 \(=\)
\(=\) 
- Louis: "How is \( \dfrac{1}{2} \) easier?"
- Hugo: "Because \( \dfrac{1}{2} \) is the simplified form of \( \dfrac{6}{12} \). It means you ate 1 out of 2 slices instead of 6 out of 12 slices. It’s the same amount of pizza, but it’s simpler to understand!"
Method Simplifying a fraction
To simplify a fraction, we find an equivalent fraction with the smallest possible numerator and denominator.
Example
Simplify \(\dfrac{4}{6}\)
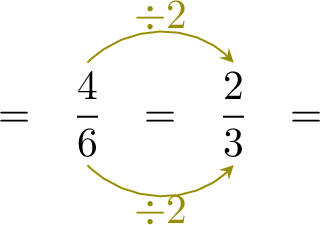
Ordering Fractions
- Hugo eats \(\dfrac{3}{4}\) of a cake.

- Louis eats \(\dfrac{5}{8}\) of the same cake.

- We need to compare the fractions \(\dfrac{3}{4}\) and \(\dfrac{5}{8}\).
- To compare fractions, the pieces must be the same size. We do this by finding a common denominator.
- Convert \(\dfrac{3}{4}\) to an equivalent fraction with denominator 8:
 \quad
\quad 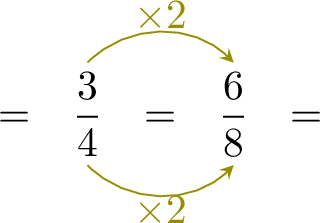 \quad
\quad 
- Now, Hugo eats \(\dfrac{6}{8}\) of the cake and Louis eats \(\dfrac{5}{8}\).
- Since \(\dfrac{6}{8} > \dfrac{5}{8}\), Hugo eats more cake.
Definition Ordering Fractions with the Same Denominator
For two fractions with the same denominator, the fraction with the larger numerator is larger.
Example
Compare \(\dfrac{3}{4}\) and \(\dfrac{2}{4}\).
Method Comparing Fractions with Different Denominators
To compare two fractions with different denominators:
- Find a common denominator.
- Convert each fraction to an equivalent fraction with that denominator.
- Compare the numerators.
Example
Compare \(\dfrac{1}{2}\) and \(\dfrac{3}{4}\).
- Since \(\dfrac{1}{2}\) and \(\dfrac{3}{4}\) have different denominators, we change \(\dfrac{1}{2}\) into an equivalent fraction with denominator 4:
 \quad
\quad 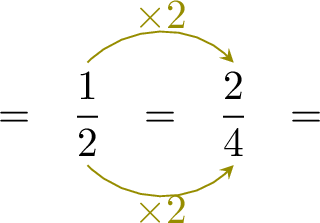 \quad
\quad 
- Compare the numerators: \[\dfrac{2}{4} < \dfrac{3}{4}\]
- Therefore, \[\dfrac{1}{2} < \dfrac{3}{4}\]
- In pictures:
 \quad = \quad
\quad = \quad  \quad < \quad
\quad < \quad 
Addition and Subtraction with Common Denominators
Hugo eats \(\dfrac{2}{4}\) of a cake:  and Louis eats \(\dfrac{1}{4}\) of the same cake:
and Louis eats \(\dfrac{1}{4}\) of the same cake: 
Which fraction of the cake have Hugo and Louis eaten together?
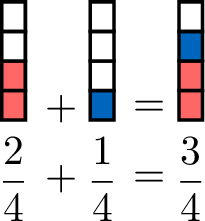

Which fraction of the cake have Hugo and Louis eaten together?
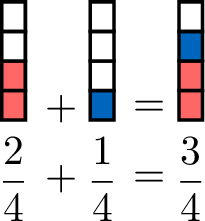
Definition Addition of Fractions with Common Denominators
When we add fractions with common denominators, we keep the denominator the same and add the numerators: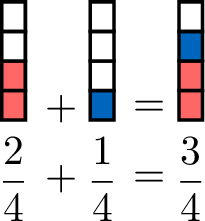
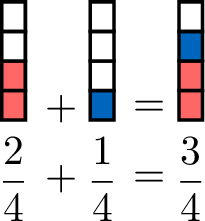
Definition Subtraction of Fractions with Common Denominators
When we subtract fractions with common denominators, we keep the denominator the same and subtract the numerators: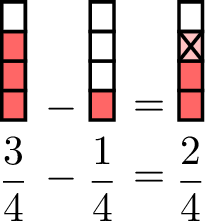
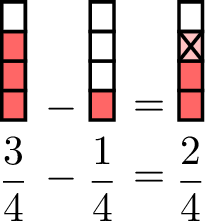
Addition and Subtraction with Different Denominators
Hugo eats \(\dfrac{1}{2}\) of a cake:  and Louis eats \(\dfrac{1}{4}\) of the same cake:
and Louis eats \(\dfrac{1}{4}\) of the same cake:  .
.
What fraction of the cake have Hugo and Louis eaten together?
What fraction of the cake have Hugo and Louis eaten together?
- Step 1: Find a common denominator: To add the fractions, we need equal-sized parts. Divide each of Hugo's parts into two smaller parts:
 \quad \(=\) \quad
\quad \(=\) \quad
- Step 2: Add the fractions using the common denominator: Now, we can add the two fractions:
 \(+\)
\(+\) 
\(=\)  \(+\)
\(+\) 
\(=\) 
\(\dfrac{1}{2}+\dfrac{1}{4}\) \(=\) \(\dfrac{2}{4}+\dfrac{1}{4}\) \(=\) \(\dfrac{3}{4}\) - Step 3: Final Answer: Hugo and Louis eat \(\dfrac{3}{4}\) of the cake together:

Method Addition or Subtraction of Fractions with Different Denominators
To add or subtract fractions with different denominators:
- Find a common denominator: Choose a common multiple of the denominators.
- Convert each fraction: Rewrite each fraction so it has the common denominator.
- Add or subtract the numerators: Add or subtract the numerators and keep the denominator the same.