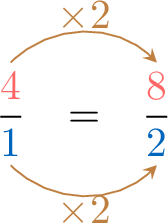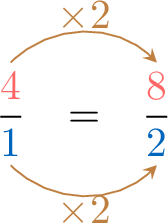Ratios
Definition
Definition Ratio
A ratio is a comparison of two quantities. The ratio \(\textcolor{colordef}{3}\) to \(\textcolor{colorprop}{2}\) can be expressed as \(\textcolor{colordef}{3}:\textcolor{colorprop}{2}\) or \(\dfrac{\textcolor{colordef}{3}}{\textcolor{colorprop}{2}}\).
Part-part and Part-whole Ratios
Definition Part-part Ratio
A part-part ratio compares two distinct parts of a whole.$$\textcolor{colordef}{\text{Part 1}}:\textcolor{colorprop}{\text{Part 2}}$$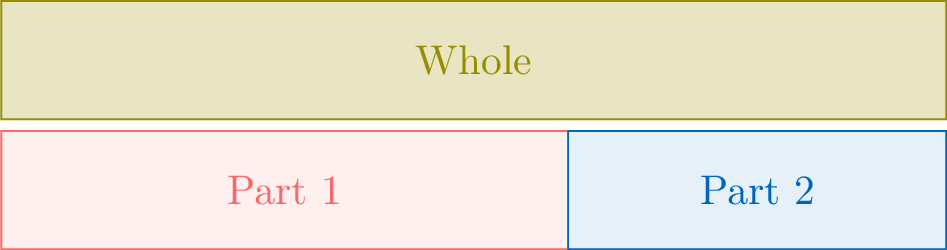
Example
For one bowl of fruit juice, there are \(\textcolor{colordef}{3}\) cherries and \(\textcolor{colorprop}{2}\) apples.
Definition Part-whole Ratio
A Part-whole ratio compares one part of a whole to the whole.$$\textcolor{colordef}{\text{Part 1}}:\textcolor{olive}{\text{Whole}}\text{ or }\textcolor{colorprop}{\text{Part 2}}:\textcolor{olive}{\text{Whole}}$$
Example
If a juice is made with \(\textcolor{yellow}{1}\) lemon and \(\textcolor{orange}{2}\) oranges, find the ratio of oranges to the total number of fruits.
- The total number of fruits is \(\textcolor{yellow}{1}+\textcolor{orange}{2} = 3\).
- The ratio of oranges to the total number of fruits is \(\dfrac{\textcolor{orange}{2}}{3}\).
Equal Ratios
- Let's make some fresh juice! For one glass of juice, we need \(\textcolor{yellow}{1}\) lemon and \(\textcolor{orange}{2}\) oranges. The ratio of lemons to oranges is \(\textcolor{yellow}{1}:\textcolor{orange}{2}\).
- Now, if we want to make two glasses of juice, we need to double the ingredients.
- The ratio remains the same. The ratios are equal: \(\textcolor{yellow}{1}:\textcolor{orange}{2}=\textcolor{yellow}{2}:\textcolor{orange}{4}\).
Definition Equal Ratios
Two ratios are equal if one can be expressed as a multiple of the other.
Method Using Fractions
To show that two ratios are equal, we can compare their related fractions. If the fractions are equal, then the ratios are equal.
Example
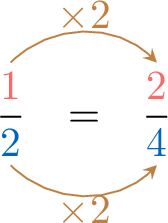, \(\textcolor{colordef}{1}:\textcolor{colorprop}{2}=\textcolor{colordef}{2}:\textcolor{colorprop}{4}\)Proportion
Imagine you're making a fruit juice mix. The recipe calls for \(\textcolor{orange}{4}\) cups of orange juice and \(\textcolor{olive}{2}\) cups of apple juice. This ratio of \(\textcolor{orange}{4}:\textcolor{olive}{2}\) ensures the juice has the right flavor balance.But what if you want to make a larger batch? If you double the amount of orange juice, how much apple juice will you need to keep the same taste? Write your answer as a number of cups.
If you double the amount of orange juice from \(\textcolor{orange}{4}\) cups to \(\textcolor{orange}{8}\) cups, you also need to double the amount of apple juice from \(\textcolor{olive}{2}\) cups to \(\textcolor{olive}{4}\) cups to keep the same taste.
So, the new ratio is \(\textcolor{orange}{8}:\textcolor{olive}{4}\), which is the same as the original ratio \(\textcolor{orange}{4}:\textcolor{olive}{2}\).
So, the new ratio is \(\textcolor{orange}{8}:\textcolor{olive}{4}\), which is the same as the original ratio \(\textcolor{orange}{4}:\textcolor{olive}{2}\).
Definition Proportion
A proportion states that two ratios are equal.
Example
To make \(\textcolor{colorprop}{1}\) chocolate cake, \(\textcolor{colordef}{4}\) eggs are needed. How many eggs are needed to make \(\textcolor{colorprop}{2}\) cakes?
For \(\textcolor{colorprop}{1}\) cake, it takes \(\textcolor{colordef}{4}\) eggs. Therefore, to maintain this proportion for \(\textcolor{colorprop}{2}\) cakes, multiply both the number of cakes and the number of eggs by \(\textcolor{brown}{2}\):